Minimally Modifying a Markov Game to Achieve Any Nash Equilibrium and Value

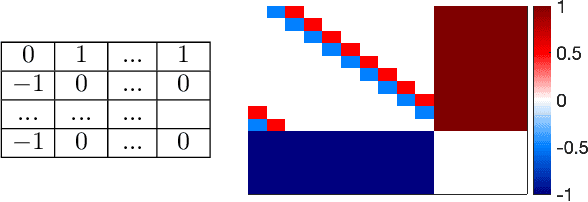
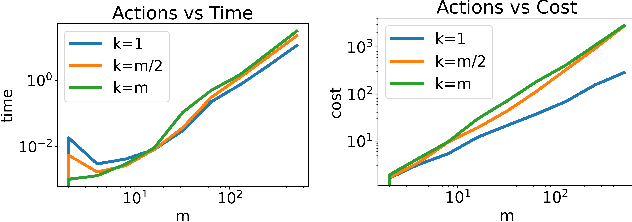
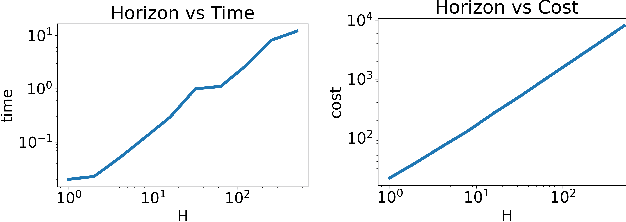
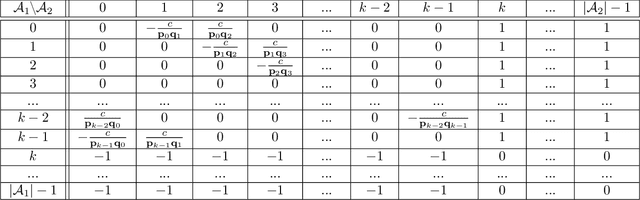
We study the game modification problem, where a benevolent game designer or a malevolent adversary modifies the reward function of a zero-sum Markov game so that a target deterministic or stochastic policy profile becomes the unique Markov perfect Nash equilibrium and has a value within a target range, in a way that minimizes the modification cost. We characterize the set of policy profiles that can be installed as the unique equilibrium of some game, and establish sufficient and necessary conditions for successful installation. We propose an efficient algorithm, which solves a convex optimization problem with linear constraints and then performs random perturbation, to obtain a modification plan with a near-optimal cost.