Comparing Reinforcement Learning and Human Learning using the Game of Hidden Rules

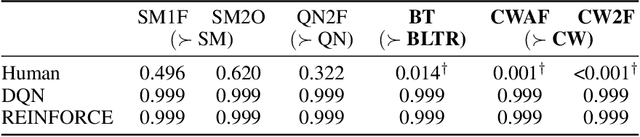
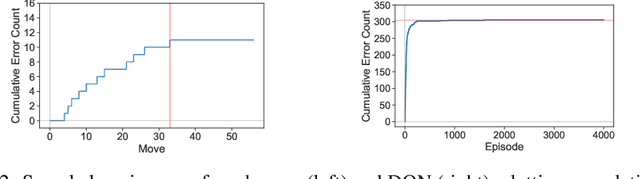
Reliable real-world deployment of reinforcement learning (RL) methods requires a nuanced understanding of their strengths and weaknesses and how they compare to those of humans. Human-machine systems are becoming more prevalent and the design of these systems relies on a task-oriented understanding of both human learning (HL) and RL. Thus, an important line of research is characterizing how the structure of a learning task affects learning performance. While increasingly complex benchmark environments have led to improved RL capabilities, such environments are difficult to use for the dedicated study of task structure. To address this challenge we present a learning environment built to support rigorous study of the impact of task structure on HL and RL. We demonstrate the environment's utility for such study through example experiments in task structure that show performance differences between humans and RL algorithms.

The Game of Hidden Rules: A New Kind of Benchmark Challenge for Machine Learning

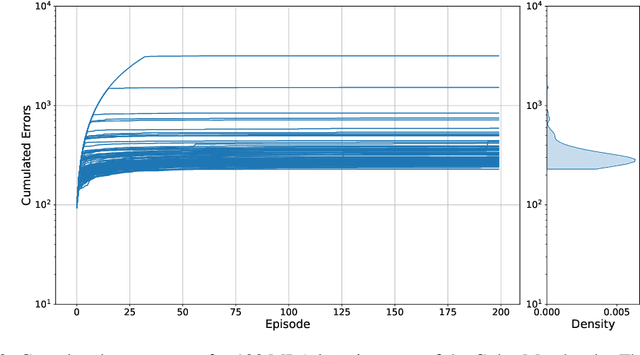
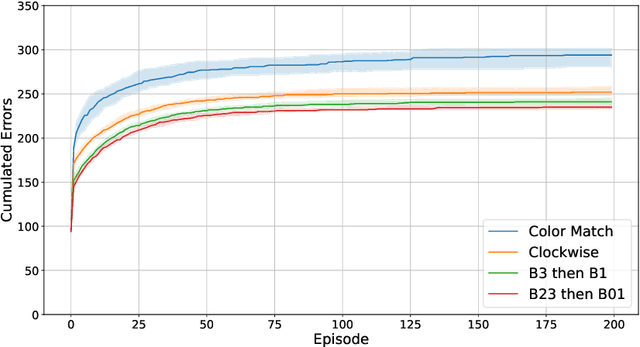
As machine learning (ML) is more tightly woven into society, it is imperative that we better characterize ML's strengths and limitations if we are to employ it responsibly. Existing benchmark environments for ML, such as board and video games, offer well-defined benchmarks for progress, but constituent tasks are often complex, and it is frequently unclear how task characteristics contribute to overall difficulty for the machine learner. Likewise, without a systematic assessment of how task characteristics influence difficulty, it is challenging to draw meaningful connections between performance in different benchmark environments. We introduce a novel benchmark environment that offers an enormous range of ML challenges and enables precise examination of how task elements influence practical difficulty. The tool frames learning tasks as a "board-clearing game," which we call the Game of Hidden Rules (GOHR). The environment comprises an expressive rule language and a captive server environment that can be installed locally. We propose a set of benchmark rule-learning tasks and plan to support a performance leader-board for researchers interested in attempting to learn our rules. GOHR complements existing environments by allowing fine, controlled modifications to tasks, enabling experimenters to better understand how each facet of a given learning task contributes to its practical difficulty for an arbitrary ML algorithm.

Ontology alignment: A Content-Based Bayesian Approach

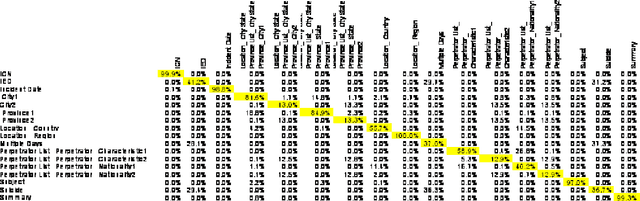
There are many legacy databases, and related stores of information that are maintained by distinct organizations, and there are other organizations that would like to be able to access and use those disparate sources. Among the examples of current interest are such things as emergency room records, of interest in tracking and interdicting illicit drugs, or social media public posts that indicate preparation and intention for a mass shooting incident. In most cases, this information is discovered too late to be useful. While agencies responsible for coordination are aware of the potential value of contemporaneous access to new data, the costs of establishing a connection are prohibitive. The problem grown even worse with the proliferation of ``hash-tagging,'' which permits new labels and ontological relations to spring up overnight. While research interest has waned, the need for powerful and inexpensive tools enabling prompt access to multiple sources has grown ever more pressing. This paper describes techniques for computing alignment matrix coefficients, which relate the fields or content of one database to those of another, using the Bayesian Ontology Alignment tool (BOA). Particular attention is given to formulas that have an easy-to-understand meaning when all cells of the data sources containing values from some small set. These formulas can be expressed in terms of probability estimates. The estimates themselves are given by a ``black box'' polytomous logistic regression model (PLRM), and thus can be easily generalized to the case of any arbitrary probability-generating model. The specific PLRM model used in this example is the BOXER Bayesian Extensible Online Regression model.