Diffusing States and Matching Scores: A New Framework for Imitation Learning

Adversarial Imitation Learning is traditionally framed as a two-player zero-sum game between a learner and an adversarially chosen cost function, and can therefore be thought of as the sequential generalization of a Generative Adversarial Network (GAN). A prominent example of this framework is Generative Adversarial Imitation Learning (GAIL). However, in recent years, diffusion models have emerged as a non-adversarial alternative to GANs that merely require training a score function via regression, yet produce generations of a higher quality. In response, we investigate how to lift insights from diffusion modeling to the sequential setting. We propose diffusing states and performing score-matching along diffused states to measure the discrepancy between the expert's and learner's states. Thus, our approach only requires training score functions to predict noises via standard regression, making it significantly easier and more stable to train than adversarial methods. Theoretically, we prove first- and second-order instance-dependent bounds with linear scaling in the horizon, proving that our approach avoids the compounding errors that stymie offline approaches to imitation learning. Empirically, we show our approach outperforms GAN-style imitation learning baselines across various continuous control problems, including complex tasks like controlling humanoids to walk, sit, and crawl.

Computationally Efficient RL under Linear Bellman Completeness for Deterministic Dynamics

We study computationally and statistically efficient Reinforcement Learning algorithms for the linear Bellman Complete setting, a setting that uses linear function approximation to capture value functions and unifies existing models like linear Markov Decision Processes (MDP) and Linear Quadratic Regulators (LQR). While it is known from the prior works that this setting is statistically tractable, it remained open whether a computationally efficient algorithm exists. Our work provides a computationally efficient algorithm for the linear Bellman complete setting that works for MDPs with large action spaces, random initial states, and random rewards but relies on the underlying dynamics to be deterministic. Our approach is based on randomization: we inject random noise into least square regression problems to perform optimistic value iteration. Our key technical contribution is to carefully design the noise to only act in the null space of the training data to ensure optimism while circumventing a subtle error amplification issue.

Making RL with Preference-based Feedback Efficient via Randomization

Reinforcement Learning algorithms that learn from human feedback (RLHF) need to be efficient in terms of statistical complexity, computational complexity, and query complexity. In this work, we consider the RLHF setting where the feedback is given in the format of preferences over pairs of trajectories. In the linear MDP model, by using randomization in algorithm design, we present an algorithm that is sample efficient (i.e., has near-optimal worst-case regret bounds) and has polynomial running time (i.e., computational complexity is polynomial with respect to relevant parameters). Our algorithm further minimizes the query complexity through a novel randomized active learning procedure. In particular, our algorithm demonstrates a near-optimal tradeoff between the regret bound and the query complexity. To extend the results to more general nonlinear function approximation, we design a model-based randomized algorithm inspired by the idea of Thompson sampling. Our algorithm minimizes Bayesian regret bound and query complexity, again achieving a near-optimal tradeoff between these two quantities. Computation-wise, similar to the prior Thompson sampling algorithms under the regular RL setting, the main computation primitives of our algorithm are Bayesian supervised learning oracles which have been heavily investigated on the empirical side when applying Thompson sampling algorithms to RL benchmark problems.

Contextual Bandits and Imitation Learning via Preference-Based Active Queries

We consider the problem of contextual bandits and imitation learning, where the learner lacks direct knowledge of the executed action's reward. Instead, the learner can actively query an expert at each round to compare two actions and receive noisy preference feedback. The learner's objective is two-fold: to minimize the regret associated with the executed actions, while simultaneously, minimizing the number of comparison queries made to the expert. In this paper, we assume that the learner has access to a function class that can represent the expert's preference model under appropriate link functions, and provide an algorithm that leverages an online regression oracle with respect to this function class for choosing its actions and deciding when to query. For the contextual bandit setting, our algorithm achieves a regret bound that combines the best of both worlds, scaling as $O(\min\{\sqrt{T}, d/\Delta\})$, where $T$ represents the number of interactions, $d$ represents the eluder dimension of the function class, and $\Delta$ represents the minimum preference of the optimal action over any suboptimal action under all contexts. Our algorithm does not require the knowledge of $\Delta$, and the obtained regret bound is comparable to what can be achieved in the standard contextual bandits setting where the learner observes reward signals at each round. Additionally, our algorithm makes only $O(\min\{T, d^2/\Delta^2\})$ queries to the expert. We then extend our algorithm to the imitation learning setting, where the learning agent engages with an unknown environment in episodes of length $H$ each, and provide similar guarantees for regret and query complexity. Interestingly, our algorithm for imitation learning can even learn to outperform the underlying expert, when it is suboptimal, highlighting a practical benefit of preference-based feedback in imitation learning.

Selective Sampling and Imitation Learning via Online Regression

We consider the problem of Imitation Learning (IL) by actively querying noisy expert for feedback. While imitation learning has been empirically successful, much of prior work assumes access to noiseless expert feedback which is not practical in many applications. In fact, when one only has access to noisy expert feedback, algorithms that rely on purely offline data (non-interactive IL) can be shown to need a prohibitively large number of samples to be successful. In contrast, in this work, we provide an interactive algorithm for IL that uses selective sampling to actively query the noisy expert for feedback. Our contributions are twofold: First, we provide a new selective sampling algorithm that works with general function classes and multiple actions, and obtains the best-known bounds for the regret and the number of queries. Next, we extend this analysis to the problem of IL with noisy expert feedback and provide a new IL algorithm that makes limited queries. Our algorithm for selective sampling leverages function approximation, and relies on an online regression oracle w.r.t.~the given model class to predict actions, and to decide whether to query the expert for its label. On the theoretical side, the regret bound of our algorithm is upper bounded by the regret of the online regression oracle, while the query complexity additionally depends on the eluder dimension of the model class. We complement this with a lower bound that demonstrates that our results are tight. We extend our selective sampling algorithm for IL with general function approximation and provide bounds on both the regret and the number of queries made to the noisy expert. A key novelty here is that our regret and query complexity bounds only depend on the number of times the optimal policy (and not the noisy expert, or the learner) go to states that have a small margin.

The Benefits of Being Distributional: Small-Loss Bounds for Reinforcement Learning

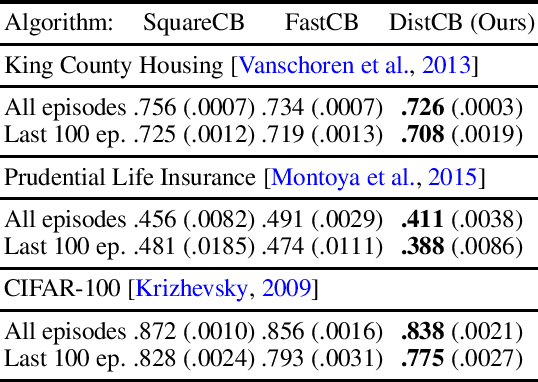
While distributional reinforcement learning (RL) has demonstrated empirical success, the question of when and why it is beneficial has remained unanswered. In this work, we provide one explanation for the benefits of distributional RL through the lens of small-loss bounds, which scale with the instance-dependent optimal cost. If the optimal cost is small, our bounds are stronger than those from non-distributional approaches. As warmup, we show that learning the cost distribution leads to small-loss regret bounds in contextual bandits (CB), and we find that distributional CB empirically outperforms the state-of-the-art on three challenging tasks. For online RL, we propose a distributional version-space algorithm that constructs confidence sets using maximum likelihood estimation, and we prove that it achieves small-loss regret in the tabular MDPs and enjoys small-loss PAC bounds in latent variable models. Building on similar insights, we propose a distributional offline RL algorithm based on the pessimism principle and prove that it enjoys small-loss PAC bounds, which exhibit a novel robustness property. For both online and offline RL, our results provide the first theoretical benefits of learning distributions even when we only need the mean for making decisions.

Distributional Offline Policy Evaluation with Predictive Error Guarantees

We study the problem of estimating the distribution of the return of a policy using an offline dataset that is not generated from the policy, i.e., distributional offline policy evaluation (OPE). We propose an algorithm called Fitted Likelihood Estimation (FLE), which conducts a sequence of Maximum Likelihood Estimation (MLE) problems and has the flexibility of integrating any state-of-art probabilistic generative models as long as it can be trained via MLE. FLE can be used for both finite horizon and infinite horizon discounted settings where rewards can be multi-dimensional vectors. In our theoretical results, we show that for both finite and infinite horizon discounted settings, FLE can learn distributions that are close to the ground truth under total variation distance and Wasserstein distance, respectively. Our theoretical results hold under the conditions that the offline data covers the test policy's traces and the supervised learning MLE procedures succeed. Experimentally, we demonstrate the performance of FLE with two generative models, Gaussian mixture models and diffusion models. For the multi-dimensional reward setting, FLE with diffusion models is capable of estimating the complicated distribution of the return of a test policy.

MALib: A Parallel Framework for Population-based Multi-agent Reinforcement Learning

Population-based multi-agent reinforcement learning (PB-MARL) refers to the series of methods nested with reinforcement learning (RL) algorithms, which produces a self-generated sequence of tasks arising from the coupled population dynamics. By leveraging auto-curricula to induce a population of distinct emergent strategies, PB-MARL has achieved impressive success in tackling multi-agent tasks. Despite remarkable prior arts of distributed RL frameworks, PB-MARL poses new challenges for parallelizing the training frameworks due to the additional complexity of multiple nested workloads between sampling, training and evaluation involved with heterogeneous policy interactions. To solve these problems, we present MALib, a scalable and efficient computing framework for PB-MARL. Our framework is comprised of three key components: (1) a centralized task dispatching model, which supports the self-generated tasks and scalable training with heterogeneous policy combinations; (2) a programming architecture named Actor-Evaluator-Learner, which achieves high parallelism for both training and sampling, and meets the evaluation requirement of auto-curriculum learning; (3) a higher-level abstraction of MARL training paradigms, which enables efficient code reuse and flexible deployments on different distributed computing paradigms. Experiments on a series of complex tasks such as multi-agent Atari Games show that MALib achieves throughput higher than 40K FPS on a single machine with $32$ CPU cores; 5x speedup than RLlib and at least 3x speedup than OpenSpiel in multi-agent training tasks. MALib is publicly available at https://github.com/sjtu-marl/malib.