The Benefits of Being Distributional: Small-Loss Bounds for Reinforcement Learning

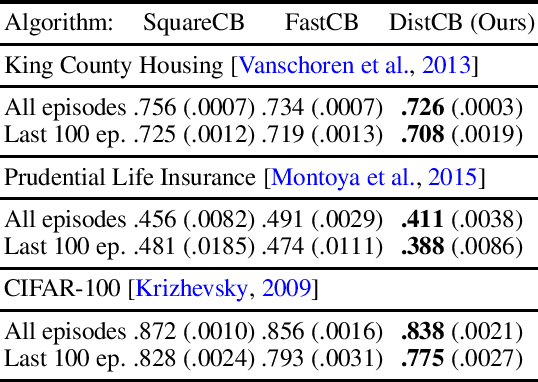
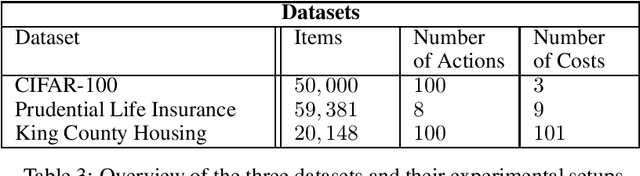
While distributional reinforcement learning (RL) has demonstrated empirical success, the question of when and why it is beneficial has remained unanswered. In this work, we provide one explanation for the benefits of distributional RL through the lens of small-loss bounds, which scale with the instance-dependent optimal cost. If the optimal cost is small, our bounds are stronger than those from non-distributional approaches. As warmup, we show that learning the cost distribution leads to small-loss regret bounds in contextual bandits (CB), and we find that distributional CB empirically outperforms the state-of-the-art on three challenging tasks. For online RL, we propose a distributional version-space algorithm that constructs confidence sets using maximum likelihood estimation, and we prove that it achieves small-loss regret in the tabular MDPs and enjoys small-loss PAC bounds in latent variable models. Building on similar insights, we propose a distributional offline RL algorithm based on the pessimism principle and prove that it enjoys small-loss PAC bounds, which exhibit a novel robustness property. For both online and offline RL, our results provide the first theoretical benefits of learning distributions even when we only need the mean for making decisions.