$Q\sharp$: Provably Optimal Distributional RL for LLM Post-Training

Reinforcement learning (RL) post-training is crucial for LLM alignment and reasoning, but existing policy-based methods, such as PPO and DPO, can fall short of fixing shortcuts inherited from pre-training. In this work, we introduce $Q\sharp$, a value-based algorithm for KL-regularized RL that guides the reference policy using the optimal regularized $Q$ function. We propose to learn the optimal $Q$ function using distributional RL on an aggregated online dataset. Unlike prior value-based baselines that guide the model using unregularized $Q$-values, our method is theoretically principled and provably learns the optimal policy for the KL-regularized RL problem. Empirically, $Q\sharp$ outperforms prior baselines in math reasoning benchmarks while maintaining a smaller KL divergence to the reference policy. Theoretically, we establish a reduction from KL-regularized RL to no-regret online learning, providing the first bounds for deterministic MDPs under only realizability. Thanks to distributional RL, our bounds are also variance-dependent and converge faster when the reference policy has small variance. In sum, our results highlight $Q\sharp$ as an effective approach for post-training LLMs, offering both improved performance and theoretical guarantees. The code can be found at https://github.com/jinpz/q_sharp.

Divide and Merge: Motion and Semantic Learning in End-to-End Autonomous Driving

Perceiving the environment and its changes over time corresponds to two fundamental yet heterogeneous types of information: semantics and motion. Previous end-to-end autonomous driving works represent both types of information in a single feature vector. However, including motion tasks, such as prediction and planning, always impairs detection and tracking performance, a phenomenon known as negative transfer in multi-task learning. To address this issue, we propose Neural-Bayes motion decoding, a novel parallel detection, tracking, and prediction method separating semantic and motion learning, similar to the Bayes filter. Specifically, we employ a set of learned motion queries that operate in parallel with the detection and tracking queries, sharing a unified set of recursively updated reference points. Moreover, we employ interactive semantic decoding to enhance information exchange in semantic tasks, promoting positive transfer. Experiments on the nuScenes dataset show improvements of 5% in detection and 11% in tracking. Our method achieves state-of-the-art collision rates in open-loop planning evaluation without any modifications to the planning module.

Adversarial Attacked Teacher for Unsupervised Domain Adaptive Object Detection

Object detectors encounter challenges in handling domain shifts. Cutting-edge domain adaptive object detection methods use the teacher-student framework and domain adversarial learning to generate domain-invariant pseudo-labels for self-training. However, the pseudo-labels generated by the teacher model tend to be biased towards the majority class and often mistakenly include overconfident false positives and underconfident false negatives. We reveal that pseudo-labels vulnerable to adversarial attacks are more likely to be low-quality. To address this, we propose a simple yet effective framework named Adversarial Attacked Teacher (AAT) to improve the quality of pseudo-labels. Specifically, we apply adversarial attacks to the teacher model, prompting it to generate adversarial pseudo-labels to correct bias, suppress overconfidence, and encourage underconfident proposals. An adaptive pseudo-label regularization is introduced to emphasize the influence of pseudo-labels with high certainty and reduce the negative impacts of uncertain predictions. Moreover, robust minority objects verified by pseudo-label regularization are oversampled to minimize dataset imbalance without introducing false positives. Extensive experiments conducted on various datasets demonstrate that AAT achieves superior performance, reaching 52.6 mAP on Clipart1k, surpassing the previous state-of-the-art by 6.7%.

Conditioned Language Policy: A General Framework for Steerable Multi-Objective Finetuning

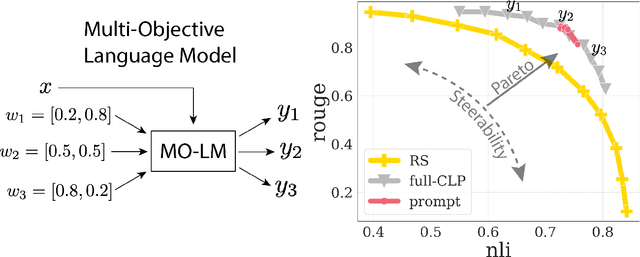
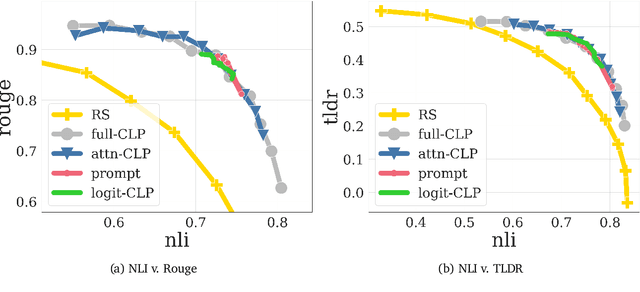
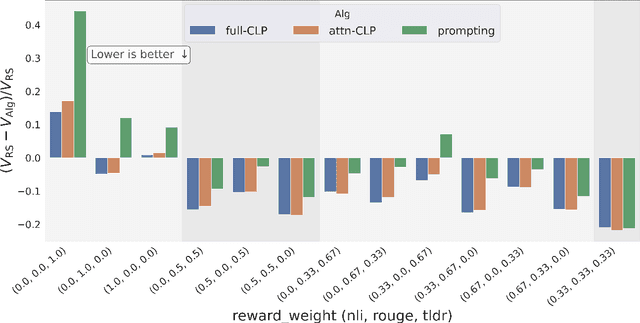
Reward-based finetuning is crucial for aligning language policies with intended behaviors (e.g., creativity and safety). A key challenge here is to develop steerable language models that trade-off multiple (conflicting) objectives in a flexible and efficient manner. This paper presents Conditioned Language Policy (CLP), a general framework for finetuning language models on multiple objectives. Building on techniques from multi-task training and parameter-efficient finetuning, CLP can learn steerable models that effectively trade-off conflicting objectives at inference time. Notably, this does not require training or maintaining multiple models to achieve different trade-offs between the objectives. Through an extensive set of experiments and ablations, we show that the CLP framework learns steerable models that outperform and Pareto-dominate the current state-of-the-art approaches for multi-objective finetuning.

Efficient and Sharp Off-Policy Evaluation in Robust Markov Decision Processes

We study evaluating a policy under best- and worst-case perturbations to a Markov decision process (MDP), given transition observations from the original MDP, whether under the same or different policy. This is an important problem when there is the possibility of a shift between historical and future environments, due to e.g. unmeasured confounding, distributional shift, or an adversarial environment. We propose a perturbation model that can modify transition kernel densities up to a given multiplicative factor or its reciprocal, which extends the classic marginal sensitivity model (MSM) for single time step decision making to infinite-horizon RL. We characterize the sharp bounds on policy value under this model, that is, the tightest possible bounds given by the transition observations from the original MDP, and we study the estimation of these bounds from such transition observations. We develop an estimator with several appealing guarantees: it is semiparametrically efficient, and remains so even when certain necessary nuisance functions such as worst-case Q-functions are estimated at slow nonparametric rates. It is also asymptotically normal, enabling easy statistical inference using Wald confidence intervals. In addition, when certain nuisances are estimated inconsistently we still estimate a valid, albeit possibly not sharp bounds on the policy value. We validate these properties in numeric simulations. The combination of accounting for environment shifts from train to test (robustness), being insensitive to nuisance-function estimation (orthogonality), and accounting for having only finite samples to learn from (inference) together leads to credible and reliable policy evaluation.

Adversarial Defense Teacher for Cross-Domain Object Detection under Poor Visibility Conditions

Existing object detectors encounter challenges in handling domain shifts between training and real-world data, particularly under poor visibility conditions like fog and night. Cutting-edge cross-domain object detection methods use teacher-student frameworks and compel teacher and student models to produce consistent predictions under weak and strong augmentations, respectively. In this paper, we reveal that manually crafted augmentations are insufficient for optimal teaching and present a simple yet effective framework named Adversarial Defense Teacher (ADT), leveraging adversarial defense to enhance teaching quality. Specifically, we employ adversarial attacks, encouraging the model to generalize on subtly perturbed inputs that effectively deceive the model. To address small objects under poor visibility conditions, we propose a Zoom-in Zoom-out strategy, which zooms-in images for better pseudo-labels and zooms-out images and pseudo-labels to learn refined features. Our results demonstrate that ADT achieves superior performance, reaching 54.5% mAP on Foggy Cityscapes, surpassing the previous state-of-the-art by 2.6% mAP.

Switching the Loss Reduces the Cost in Batch Reinforcement Learning

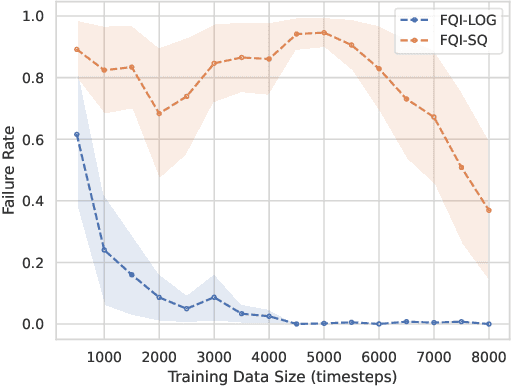
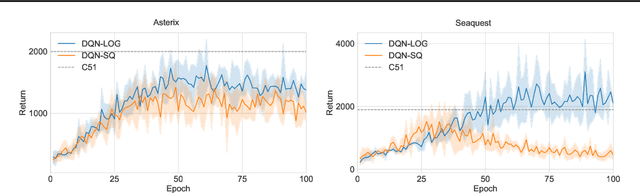
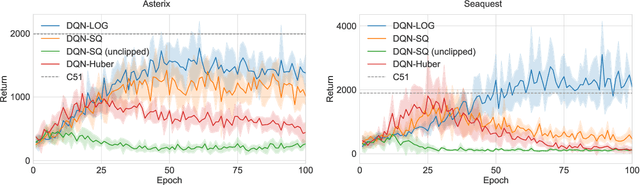
We propose training fitted Q-iteration with log-loss (FQI-LOG) for batch reinforcement learning (RL). We show that the number of samples needed to learn a near-optimal policy with FQI-LOG scales with the accumulated cost of the optimal policy, which is zero in problems where acting optimally achieves the goal and incurs no cost. In doing so, we provide a general framework for proving $\textit{small-cost}$ bounds, i.e. bounds that scale with the optimal achievable cost, in batch RL. Moreover, we empirically verify that FQI-LOG uses fewer samples than FQI trained with squared loss on problems where the optimal policy reliably achieves the goal.

Risk-Sensitive RL with Optimized Certainty Equivalents via Reduction to Standard RL

We study Risk-Sensitive Reinforcement Learning (RSRL) with the Optimized Certainty Equivalent (OCE) risk, which generalizes Conditional Value-at-risk (CVaR), entropic risk and Markowitz's mean-variance. Using an augmented Markov Decision Process (MDP), we propose two general meta-algorithms via reductions to standard RL: one based on optimistic algorithms and another based on policy optimization. Our optimistic meta-algorithm generalizes almost all prior RSRL theory with entropic risk or CVaR. Under discrete rewards, our optimistic theory also certifies the first RSRL regret bounds for MDPs with bounded coverability, e.g., exogenous block MDPs. Under discrete rewards, our policy optimization meta-algorithm enjoys both global convergence and local improvement guarantees in a novel metric that lower bounds the true OCE risk. Finally, we instantiate our framework with PPO, construct an MDP, and show that it learns the optimal risk-sensitive policy while prior algorithms provably fail.

More Benefits of Being Distributional: Second-Order Bounds for Reinforcement Learning

In this paper, we prove that Distributional Reinforcement Learning (DistRL), which learns the return distribution, can obtain second-order bounds in both online and offline RL in general settings with function approximation. Second-order bounds are instance-dependent bounds that scale with the variance of return, which we prove are tighter than the previously known small-loss bounds of distributional RL. To the best of our knowledge, our results are the first second-order bounds for low-rank MDPs and for offline RL. When specializing to contextual bandits (one-step RL problem), we show that a distributional learning based optimism algorithm achieves a second-order worst-case regret bound, and a second-order gap dependent bound, simultaneously. We also empirically demonstrate the benefit of DistRL in contextual bandits on real-world datasets. We highlight that our analysis with DistRL is relatively simple, follows the general framework of optimism in the face of uncertainty and does not require weighted regression. Our results suggest that DistRL is a promising framework for obtaining second-order bounds in general RL settings, thus further reinforcing the benefits of DistRL.

JoinGym: An Efficient Query Optimization Environment for Reinforcement Learning

In this paper, we present \textsc{JoinGym}, an efficient and lightweight query optimization environment for reinforcement learning (RL). Join order selection (JOS) is a classic NP-hard combinatorial optimization problem from database query optimization and can serve as a practical testbed for the generalization capabilities of RL algorithms. We describe how to formulate each of the left-deep and bushy variants of the JOS problem as a Markov Decision Process (MDP), and we provide an implementation adhering to the standard Gymnasium API. We highlight that our implementation \textsc{JoinGym} is completely based on offline traces of all possible joins, which enables RL practitioners to easily and quickly test their methods on a realistic data management problem without needing to setup any systems. Moreover, we also provide all possible join traces on $3300$ novel SQL queries generated from the IMDB dataset. Upon benchmarking popular RL algorithms, we find that at least one method can obtain near-optimal performance on train-set queries but their performance degrades by several orders of magnitude on test-set queries. This gap motivates further research for RL algorithms that generalize well in multi-task combinatorial optimization problems.