Efficient Adaptive Experimentation with Non-Compliance

We study the problem of estimating the average treatment effect (ATE) in adaptive experiments where treatment can only be encouraged--rather than directly assigned--via a binary instrumental variable. Building on semiparametric efficiency theory, we derive the efficiency bound for ATE estimation under arbitrary, history-dependent instrument-assignment policies, and show it is minimized by a variance-aware allocation rule that balances outcome noise and compliance variability. Leveraging this insight, we introduce AMRIV--an \textbf{A}daptive, \textbf{M}ultiply-\textbf{R}obust estimator for \textbf{I}nstrumental-\textbf{V}ariable settings with variance-optimal assignment. AMRIV pairs (i) an online policy that adaptively approximates the optimal allocation with (ii) a sequential, influence-function-based estimator that attains the semiparametric efficiency bound while retaining multiply-robust consistency. We establish asymptotic normality, explicit convergence rates, and anytime-valid asymptotic confidence sequences that enable sequential inference. Finally, we demonstrate the practical effectiveness of our approach through empirical studies, showing that adaptive instrument assignment, when combined with the AMRIV estimator, yields improved efficiency and robustness compared to existing baselines.

SCENT: Robust Spatiotemporal Learning for Continuous Scientific Data via Scalable Conditioned Neural Fields

Spatiotemporal learning is challenging due to the intricate interplay between spatial and temporal dependencies, the high dimensionality of the data, and scalability constraints. These challenges are further amplified in scientific domains, where data is often irregularly distributed (e.g., missing values from sensor failures) and high-volume (e.g., high-fidelity simulations), posing additional computational and modeling difficulties. In this paper, we present SCENT, a novel framework for scalable and continuity-informed spatiotemporal representation learning. SCENT unifies interpolation, reconstruction, and forecasting within a single architecture. Built on a transformer-based encoder-processor-decoder backbone, SCENT introduces learnable queries to enhance generalization and a query-wise cross-attention mechanism to effectively capture multi-scale dependencies. To ensure scalability in both data size and model complexity, we incorporate a sparse attention mechanism, enabling flexible output representations and efficient evaluation at arbitrary resolutions. We validate SCENT through extensive simulations and real-world experiments, demonstrating state-of-the-art performance across multiple challenging tasks while achieving superior scalability.

GST-UNet: Spatiotemporal Causal Inference with Time-Varying Confounders

Estimating causal effects from spatiotemporal data is a key challenge in fields such as public health, social policy, and environmental science, where controlled experiments are often infeasible. However, existing causal inference methods relying on observational data face significant limitations: they depend on strong structural assumptions to address spatiotemporal challenges $\unicode{x2013}$ such as interference, spatial confounding, and temporal carryover effects $\unicode{x2013}$ or fail to account for $\textit{time-varying confounders}$. These confounders, influenced by past treatments and outcomes, can themselves shape future treatments and outcomes, creating feedback loops that complicate traditional adjustment strategies. To address these challenges, we introduce the $\textbf{GST-UNet}$ ($\textbf{G}$-computation $\textbf{S}$patio-$\textbf{T}$emporal $\textbf{UNet}$), a novel end-to-end neural network framework designed to estimate treatment effects in complex spatial and temporal settings. The GST-UNet leverages regression-based iterative G-computation to explicitly adjust for time-varying confounders, providing valid estimates of potential outcomes and treatment effects. To the best of our knowledge, the GST-UNet is the first neural model to account for complex, non-linear dynamics and time-varying confounders in spatiotemporal interventions. We demonstrate the effectiveness of the GST-UNet through extensive simulation studies and showcase its practical utility with a real-world analysis of the impact of wildfire smoke on respiratory hospitalizations during the 2018 California Camp Fire. Our results highlight the potential of GST-UNet to advance spatiotemporal causal inference across a wide range of policy-driven and scientific applications.

Estimating Heterogeneous Treatment Effects by Combining Weak Instruments and Observational Data

Accurately predicting conditional average treatment effects (CATEs) is crucial in personalized medicine and digital platform analytics. Since often the treatments of interest cannot be directly randomized, observational data is leveraged to learn CATEs, but this approach can incur significant bias from unobserved confounding. One strategy to overcome these limitations is to seek latent quasi-experiments in instrumental variables (IVs) for the treatment, for example, a randomized intent to treat or a randomized product recommendation. This approach, on the other hand, can suffer from low compliance, i.e., IV weakness. Some subgroups may even exhibit zero compliance meaning we cannot instrument for their CATEs at all. In this paper we develop a novel approach to combine IV and observational data to enable reliable CATE estimation in the presence of unobserved confounding in the observational data and low compliance in the IV data, including no compliance for some subgroups. We propose a two-stage framework that first learns biased CATEs from the observational data, and then applies a compliance-weighted correction using IV data, effectively leveraging IV strength variability across covariates. We characterize the convergence rates of our method and validate its effectiveness through a simulation study. Additionally, we demonstrate its utility with real data by analyzing the heterogeneous effects of 401(k) plan participation on wealth.

Efficient and Sharp Off-Policy Evaluation in Robust Markov Decision Processes

We study evaluating a policy under best- and worst-case perturbations to a Markov decision process (MDP), given transition observations from the original MDP, whether under the same or different policy. This is an important problem when there is the possibility of a shift between historical and future environments, due to e.g. unmeasured confounding, distributional shift, or an adversarial environment. We propose a perturbation model that can modify transition kernel densities up to a given multiplicative factor or its reciprocal, which extends the classic marginal sensitivity model (MSM) for single time step decision making to infinite-horizon RL. We characterize the sharp bounds on policy value under this model, that is, the tightest possible bounds given by the transition observations from the original MDP, and we study the estimation of these bounds from such transition observations. We develop an estimator with several appealing guarantees: it is semiparametrically efficient, and remains so even when certain necessary nuisance functions such as worst-case Q-functions are estimated at slow nonparametric rates. It is also asymptotically normal, enabling easy statistical inference using Wald confidence intervals. In addition, when certain nuisances are estimated inconsistently we still estimate a valid, albeit possibly not sharp bounds on the policy value. We validate these properties in numeric simulations. The combination of accounting for environment shifts from train to test (robustness), being insensitive to nuisance-function estimation (orthogonality), and accounting for having only finite samples to learn from (inference) together leads to credible and reliable policy evaluation.

Low-Rank MDPs with Continuous Action Spaces

Low-Rank Markov Decision Processes (MDPs) have recently emerged as a promising framework within the domain of reinforcement learning (RL), as they allow for provably approximately correct (PAC) learning guarantees while also incorporating ML algorithms for representation learning. However, current methods for low-rank MDPs are limited in that they only consider finite action spaces, and give vacuous bounds as $|\mathcal{A}| \to \infty$, which greatly limits their applicability. In this work, we study the problem of extending such methods to settings with continuous actions, and explore multiple concrete approaches for performing this extension. As a case study, we consider the seminal FLAMBE algorithm (Agarwal et al., 2020), which is a reward-agnostic method for PAC RL with low-rank MDPs. We show that, without any modifications to the algorithm, we obtain similar PAC bound when actions are allowed to be continuous. Specifically, when the model for transition functions satisfies a Holder smoothness condition w.r.t. actions, and either the policy class has a uniformly bounded minimum density or the reward function is also Holder smooth, we obtain a polynomial PAC bound that depends on the order of smoothness.

B-Learner: Quasi-Oracle Bounds on Heterogeneous Causal Effects Under Hidden Confounding

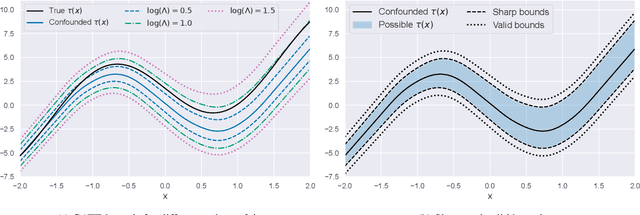
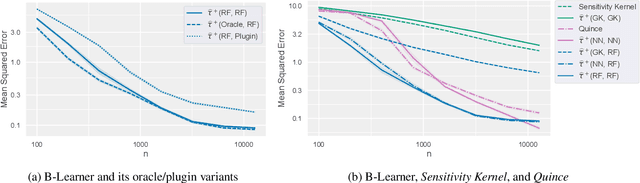
Estimating heterogeneous treatment effects from observational data is a crucial task across many fields, helping policy and decision-makers take better actions. There has been recent progress on robust and efficient methods for estimating the conditional average treatment effect (CATE) function, but these methods often do not take into account the risk of hidden confounding, which could arbitrarily and unknowingly bias any causal estimate based on observational data. We propose a meta-learner called the B-Learner, which can efficiently learn sharp bounds on the CATE function under limits on the level of hidden confounding. We derive the B-Learner by adapting recent results for sharp and valid bounds of the average treatment effect (Dorn et al., 2021) into the framework given by Kallus & Oprescu (2022) for robust and model-agnostic learning of distributional treatment effects. The B-Learner can use any function estimator such as random forests and deep neural networks, and we prove its estimates are valid, sharp, efficient, and have a quasi-oracle property with respect to the constituent estimators under more general conditions than existing methods. Semi-synthetic experimental comparisons validate the theoretical findings, and we use real-world data demonstrate how the method might be used in practice.

Adaptive Bias Correction for Improved Subseasonal Forecasting

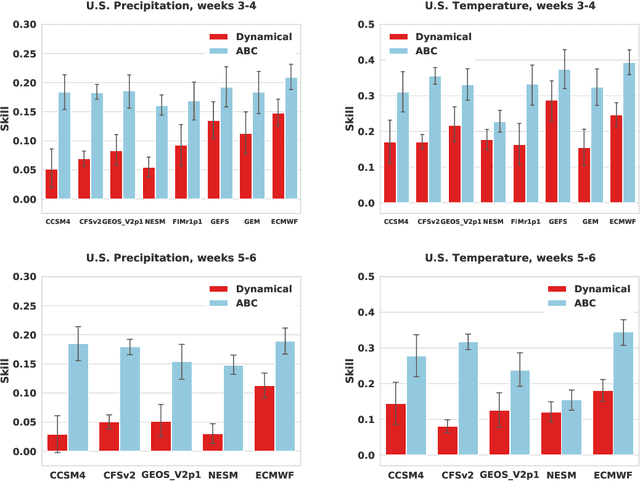
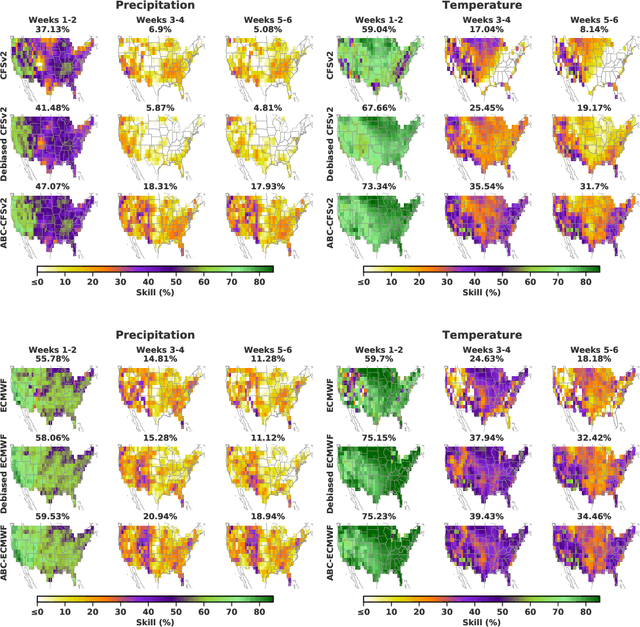
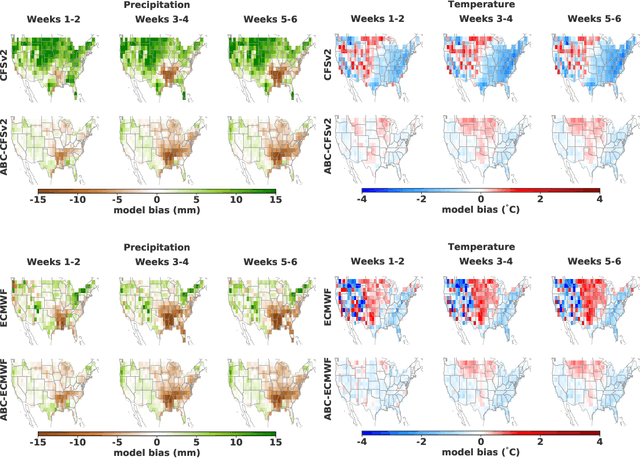
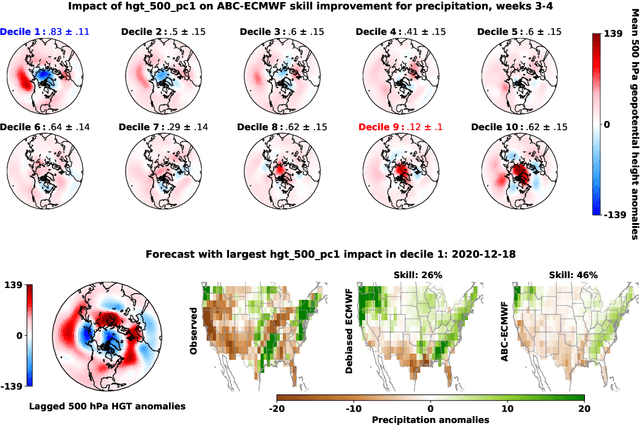
Subseasonal forecasting $\unicode{x2013}$ predicting temperature and precipitation 2 to 6 weeks $\unicode{x2013}$ ahead is critical for effective water allocation, wildfire management, and drought and flood mitigation. Recent international research efforts have advanced the subseasonal capabilities of operational dynamical models, yet temperature and precipitation prediction skills remains poor, partly due to stubborn errors in representing atmospheric dynamics and physics inside dynamical models. To counter these errors, we introduce an adaptive bias correction (ABC) method that combines state-of-the-art dynamical forecasts with observations using machine learning. When applied to the leading subseasonal model from the European Centre for Medium-Range Weather Forecasts (ECMWF), ABC improves temperature forecasting skill by 60-90% and precipitation forecasting skill by 40-69% in the contiguous U.S. We couple these performance improvements with a practical workflow, based on Cohort Shapley, for explaining ABC skill gains and identifying higher-skill windows of opportunity based on specific climate conditions.

Robust and Agnostic Learning of Conditional Distributional Treatment Effects

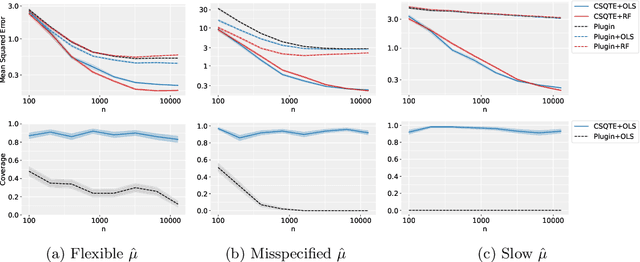
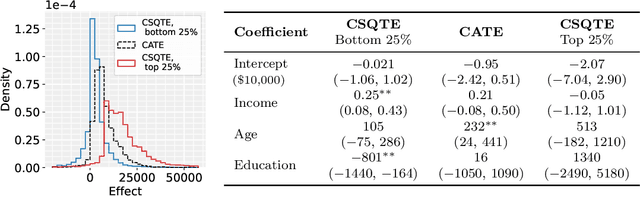
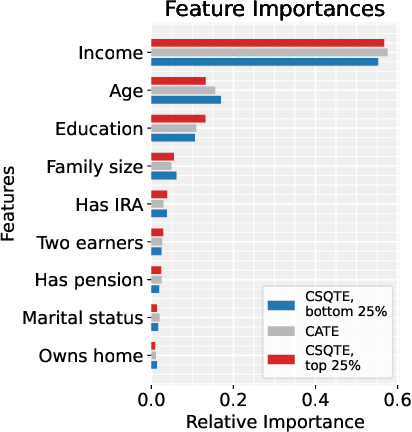
The conditional average treatment effect (CATE) is the best point prediction of individual causal effects given individual baseline covariates and can help personalize treatments. However, as CATE only reflects the (conditional) average, it can wash out potential risks and tail events, which are crucially relevant to treatment choice. In aggregate analyses, this is usually addressed by measuring distributional treatment effect (DTE), such as differences in quantiles or tail expectations between treatment groups. Hypothetically, one can similarly fit covariate-conditional quantile regressions in each treatment group and take their difference, but this would not be robust to misspecification or provide agnostic best-in-class predictions. We provide a new robust and model-agnostic methodology for learning the conditional DTE (CDTE) for a wide class of problems that includes conditional quantile treatment effects, conditional super-quantile treatment effects, and conditional treatment effects on coherent risk measures given by $f$-divergences. Our method is based on constructing a special pseudo-outcome and regressing it on baseline covariates using any given regression learner. Our method is model-agnostic in the sense that it can provide the best projection of CDTE onto the regression model class. Our method is robust in the sense that even if we learn these nuisances nonparametrically at very slow rates, we can still learn CDTEs at rates that depend on the class complexity and even conduct inferences on linear projections of CDTEs. We investigate the performance of our proposal in simulation studies, and we demonstrate its use in a case study of 401(k) eligibility effects on wealth.

Learned Benchmarks for Subseasonal Forecasting

We develop a subseasonal forecasting toolkit of simple learned benchmark models that outperform both operational practice and state-of-the-art machine learning and deep learning methods. Our new models include (a) Climatology++, an adaptive alternative to climatology that, for precipitation, is 9% more accurate and 250% more skillful than the United States operational Climate Forecasting System (CFSv2); (b) CFSv2++, a learned CFSv2 correction that improves temperature and precipitation accuracy by 7-8% and skill by 50-275%; and (c) Persistence++, an augmented persistence model that combines CFSv2 forecasts with lagged measurements to improve temperature and precipitation accuracy by 6-9% and skill by 40-130%. Across the contiguous U.S., our Climatology++, CFSv2++, and Persistence++ toolkit consistently outperforms standard meteorological baselines, state-of-the-art machine and deep learning methods, and the European Centre for Medium-Range Weather Forecasts ensemble. Overall, we find that augmenting traditional forecasting approaches with learned enhancements yields an effective and computationally inexpensive strategy for building the next generation of subseasonal forecasting benchmarks.