From Observational Data to Clinical Recommendations: A Causal Framework for Estimating Patient-level Treatment Effects and Learning Policies

We propose a framework for building patient-specific treatment recommendation models, building on the large recent literature on learning patient-level causal models and inspired by the target trial paradigm of Hernan and Robins. We focus on safety and validity, including the crucial issue of causal identification when using observational data. We do not provide a specific model, but rather a way to integrate existing methods and know-how into a practical pipeline. We further provide a real world use-case of treatment optimization for patients with heart failure who develop acute kidney injury during hospitalization. The results suggest our pipeline can improve patient outcomes over the current treatment regime.

Towards Regulatory-Confirmed Adaptive Clinical Trials: Machine Learning Opportunities and Solutions

Randomized Controlled Trials (RCTs) are the gold standard for evaluating the effect of new medical treatments. Treatments must pass stringent regulatory conditions in order to be approved for widespread use, yet even after the regulatory barriers are crossed, real-world challenges might arise: Who should get the treatment? What is its true clinical utility? Are there discrepancies in the treatment effectiveness across diverse and under-served populations? We introduce two new objectives for future clinical trials that integrate regulatory constraints and treatment policy value for both the entire population and under-served populations, thus answering some of the questions above in advance. Designed to meet these objectives, we formulate Randomize First Augment Next (RFAN), a new framework for designing Phase III clinical trials. Our framework consists of a standard randomized component followed by an adaptive one, jointly meant to efficiently and safely acquire and assign patients into treatment arms during the trial. Then, we propose strategies for implementing RFAN based on causal, deep Bayesian active learning. Finally, we empirically evaluate the performance of our framework using synthetic and real-world semi-synthetic datasets.

BIG-Bench Extra Hard

Large language models (LLMs) are increasingly deployed in everyday applications, demanding robust general reasoning capabilities and diverse reasoning skillset. However, current LLM reasoning benchmarks predominantly focus on mathematical and coding abilities, leaving a gap in evaluating broader reasoning proficiencies. One particular exception is the BIG-Bench dataset, which has served as a crucial benchmark for evaluating the general reasoning capabilities of LLMs, thanks to its diverse set of challenging tasks that allowed for a comprehensive assessment of general reasoning across various skills within a unified framework. However, recent advances in LLMs have led to saturation on BIG-Bench, and its harder version BIG-Bench Hard (BBH). State-of-the-art models achieve near-perfect scores on many tasks in BBH, thus diminishing its utility. To address this limitation, we introduce BIG-Bench Extra Hard (BBEH), a new benchmark designed to push the boundaries of LLM reasoning evaluation. BBEH replaces each task in BBH with a novel task that probes a similar reasoning capability but exhibits significantly increased difficulty. We evaluate various models on BBEH and observe a (harmonic) average accuracy of 9.8\% for the best general-purpose model and 44.8\% for the best reasoning-specialized model, indicating substantial room for improvement and highlighting the ongoing challenge of achieving robust general reasoning in LLMs. We release BBEH publicly at: https://github.com/google-deepmind/bbeh.

Heterogeneous Treatment Effect in Time-to-Event Outcomes: Harnessing Censored Data with Recursively Imputed Trees

Tailoring treatments to individual needs is a central goal in fields such as medicine. A key step toward this goal is estimating Heterogeneous Treatment Effects (HTE) - the way treatments impact different subgroups. While crucial, HTE estimation is challenging with survival data, where time until an event (e.g., death) is key. Existing methods often assume complete observation, an assumption violated in survival data due to right-censoring, leading to bias and inefficiency. Cui et al. (2023) proposed a doubly-robust method for HTE estimation in survival data under no hidden confounders, combining a causal survival forest with an augmented inverse-censoring weighting estimator. However, we find it struggles under heavy censoring, which is common in rare-outcome problems such as Amyotrophic lateral sclerosis (ALS). Moreover, most current methods cannot handle instrumental variables, which are a crucial tool in the causal inference arsenal. We introduce Multiple Imputation for Survival Treatment Response (MISTR), a novel, general, and non-parametric method for estimating HTE in survival data. MISTR uses recursively imputed survival trees to handle censoring without directly modeling the censoring mechanism. Through extensive simulations and analysis of two real-world datasets-the AIDS Clinical Trials Group Protocol 175 and the Illinois unemployment dataset we show that MISTR outperforms prior methods under heavy censoring in the no-hidden-confounders setting, and extends to the instrumental variable setting. To our knowledge, MISTR is the first non-parametric approach for HTE estimation with unobserved confounders via instrumental variables.

On the ERM Principle in Meta-Learning

Classic supervised learning involves algorithms trained on $n$ labeled examples to produce a hypothesis $h \in \mathcal{H}$ aimed at performing well on unseen examples. Meta-learning extends this by training across $n$ tasks, with $m$ examples per task, producing a hypothesis class $\mathcal{H}$ within some meta-class $\mathbb{H}$. This setting applies to many modern problems such as in-context learning, hypernetworks, and learning-to-learn. A common method for evaluating the performance of supervised learning algorithms is through their learning curve, which depicts the expected error as a function of the number of training examples. In meta-learning, the learning curve becomes a two-dimensional learning surface, which evaluates the expected error on unseen domains for varying values of $n$ (number of tasks) and $m$ (number of training examples). Our findings characterize the distribution-free learning surfaces of meta-Empirical Risk Minimizers when either $m$ or $n$ tend to infinity: we show that the number of tasks must increase inversely with the desired error. In contrast, we show that the number of examples exhibits very different behavior: it satisfies a dichotomy where every meta-class conforms to one of the following conditions: (i) either $m$ must grow inversely with the error, or (ii) a \emph{finite} number of examples per task suffices for the error to vanish as $n$ goes to infinity. This finding illustrates and characterizes cases in which a small number of examples per task is sufficient for successful learning. We further refine this for positive values of $\varepsilon$ and identify for each $\varepsilon$ how many examples per task are needed to achieve an error of $\varepsilon$ in the limit as the number of tasks $n$ goes to infinity. We achieve this by developing a necessary and sufficient condition for meta-learnability using a bounded number of examples per domain.

Is merging worth it? Securely evaluating the information gain for causal dataset acquisition

Merging datasets across institutions is a lengthy and costly procedure, especially when it involves private information. Data hosts may therefore want to prospectively gauge which datasets are most beneficial to merge with, without revealing sensitive information. For causal estimation this is particularly challenging as the value of a merge will depend not only on the reduction in epistemic uncertainty but also the improvement in overlap. To address this challenge, we introduce the first cryptographically secure information-theoretic approach for quantifying the value of a merge in the context of heterogeneous treatment effect estimation. We do this by evaluating the Expected Information Gain (EIG) and utilising multi-party computation to ensure it can be securely computed without revealing any raw data. As we demonstrate, this can be used with differential privacy (DP) to ensure privacy requirements whilst preserving more accurate computation than naive DP alone. To the best of our knowledge, this work presents the first privacy-preserving method for dataset acquisition tailored to causal estimation. We demonstrate the effectiveness and reliability of our method on a range of simulated and realistic benchmarks. The code is available anonymously.

Benchmarks for Reinforcement Learning with Biased Offline Data and Imperfect Simulators

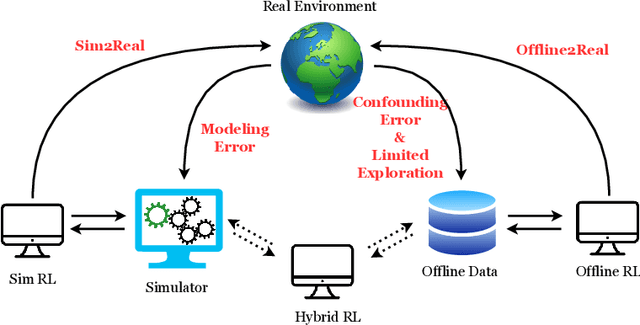
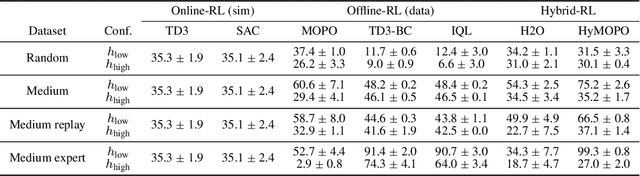
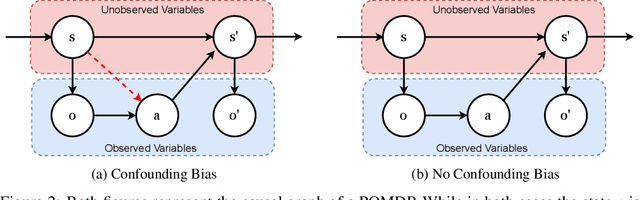
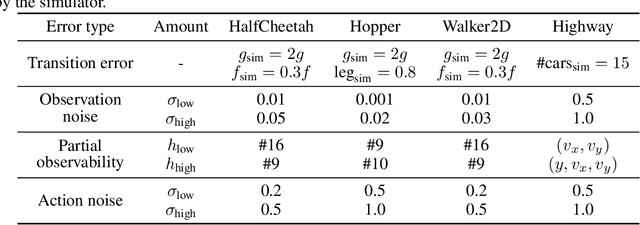
In many reinforcement learning (RL) applications one cannot easily let the agent act in the world; this is true for autonomous vehicles, healthcare applications, and even some recommender systems, to name a few examples. Offline RL provides a way to train agents without real-world exploration, but is often faced with biases due to data distribution shifts, limited coverage, and incomplete representation of the environment. To address these issues, practical applications have tried to combine simulators with grounded offline data, using so-called hybrid methods. However, constructing a reliable simulator is in itself often challenging due to intricate system complexities as well as missing or incomplete information. In this work, we outline four principal challenges for combining offline data with imperfect simulators in RL: simulator modeling error, partial observability, state and action discrepancies, and hidden confounding. To help drive the RL community to pursue these problems, we construct ``Benchmarks for Mechanistic Offline Reinforcement Learning'' (B4MRL), which provide dataset-simulator benchmarks for the aforementioned challenges. Our results suggest the key necessity of such benchmarks for future research.

Aiming for Relevance

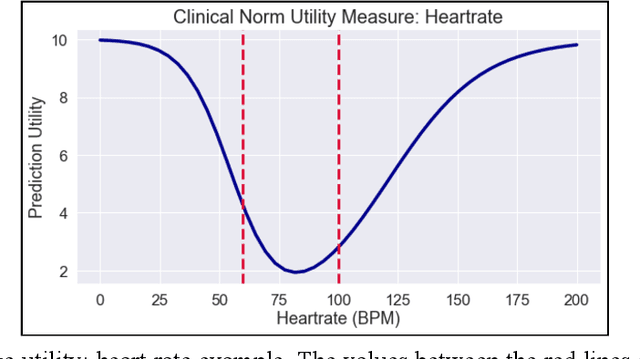
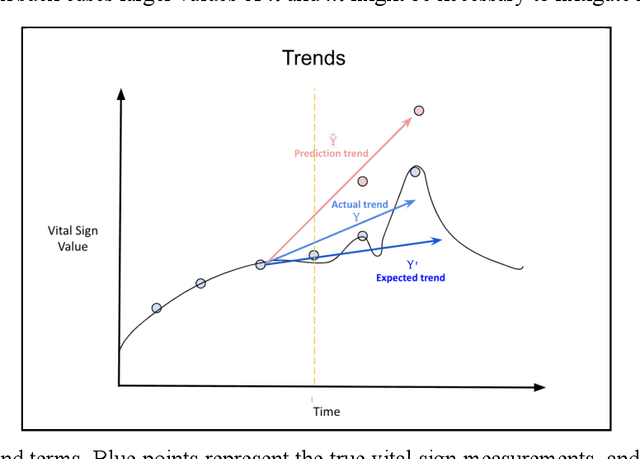
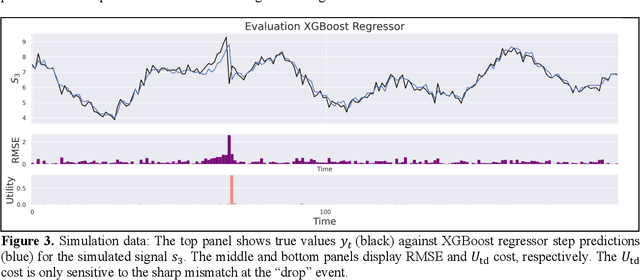
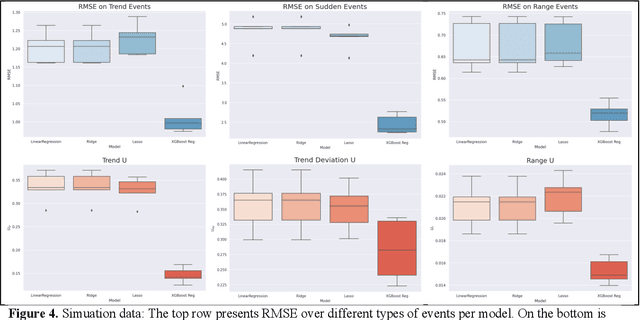
Vital signs are crucial in intensive care units (ICUs). They are used to track the patient's state and to identify clinically significant changes. Predicting vital sign trajectories is valuable for early detection of adverse events. However, conventional machine learning metrics like RMSE often fail to capture the true clinical relevance of such predictions. We introduce novel vital sign prediction performance metrics that align with clinical contexts, focusing on deviations from clinical norms, overall trends, and trend deviations. These metrics are derived from empirical utility curves obtained in a previous study through interviews with ICU clinicians. We validate the metrics' usefulness using simulated and real clinical datasets (MIMIC and eICU). Furthermore, we employ these metrics as loss functions for neural networks, resulting in models that excel in predicting clinically significant events. This research paves the way for clinically relevant machine learning model evaluation and optimization, promising to improve ICU patient care. 10 pages, 9 figures.

B-Learner: Quasi-Oracle Bounds on Heterogeneous Causal Effects Under Hidden Confounding

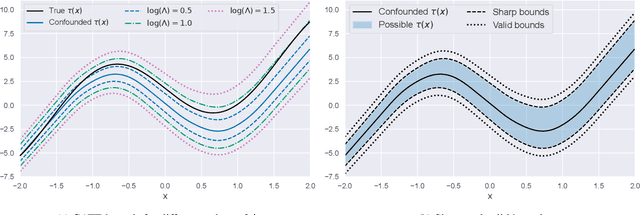
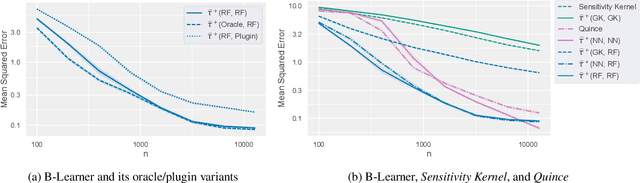
Estimating heterogeneous treatment effects from observational data is a crucial task across many fields, helping policy and decision-makers take better actions. There has been recent progress on robust and efficient methods for estimating the conditional average treatment effect (CATE) function, but these methods often do not take into account the risk of hidden confounding, which could arbitrarily and unknowingly bias any causal estimate based on observational data. We propose a meta-learner called the B-Learner, which can efficiently learn sharp bounds on the CATE function under limits on the level of hidden confounding. We derive the B-Learner by adapting recent results for sharp and valid bounds of the average treatment effect (Dorn et al., 2021) into the framework given by Kallus & Oprescu (2022) for robust and model-agnostic learning of distributional treatment effects. The B-Learner can use any function estimator such as random forests and deep neural networks, and we prove its estimates are valid, sharp, efficient, and have a quasi-oracle property with respect to the constituent estimators under more general conditions than existing methods. Semi-synthetic experimental comparisons validate the theoretical findings, and we use real-world data demonstrate how the method might be used in practice.

Malign Overfitting: Interpolation Can Provably Preclude Invariance

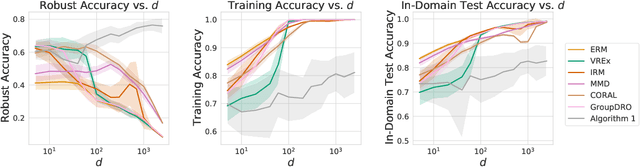
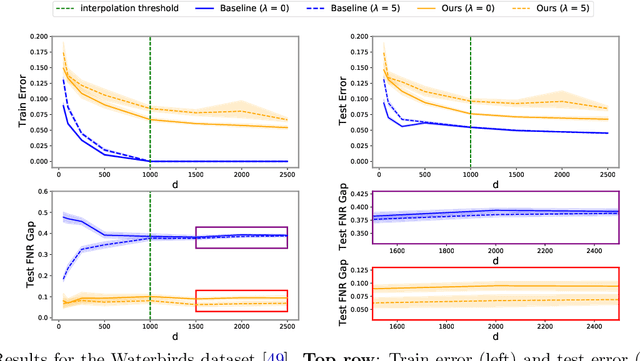
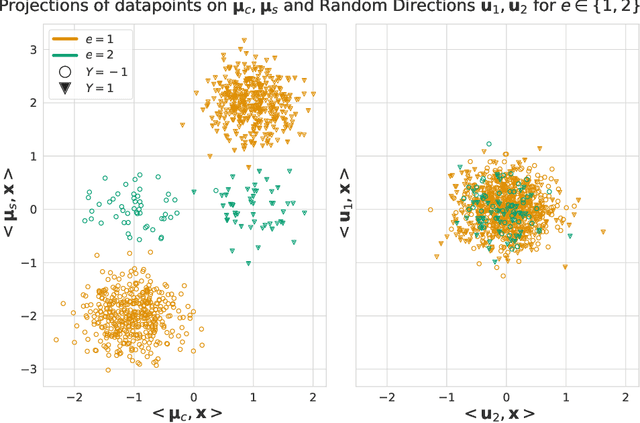
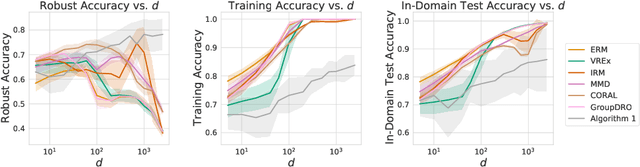
Learned classifiers should often possess certain invariance properties meant to encourage fairness, robustness, or out-of-distribution generalization. However, multiple recent works empirically demonstrate that common invariance-inducing regularizers are ineffective in the over-parameterized regime, in which classifiers perfectly fit (i.e. interpolate) the training data. This suggests that the phenomenon of ``benign overfitting," in which models generalize well despite interpolating, might not favorably extend to settings in which robustness or fairness are desirable. In this work we provide a theoretical justification for these observations. We prove that -- even in the simplest of settings -- any interpolating learning rule (with arbitrarily small margin) will not satisfy these invariance properties. We then propose and analyze an algorithm that -- in the same setting -- successfully learns a non-interpolating classifier that is provably invariant. We validate our theoretical observations on simulated data and the Waterbirds dataset.