Malign Overfitting: Interpolation Can Provably Preclude Invariance
Paper and Code
Nov 28, 2022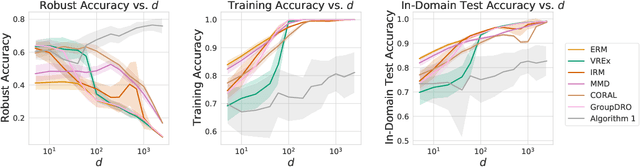
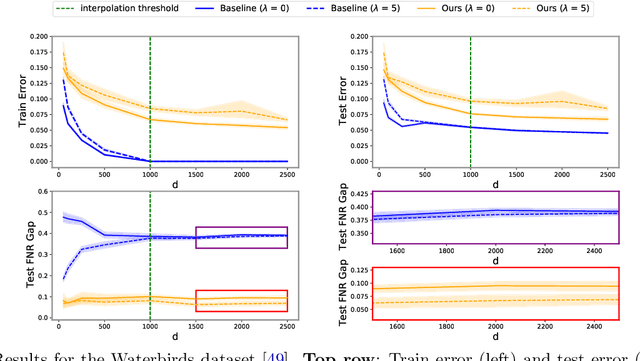
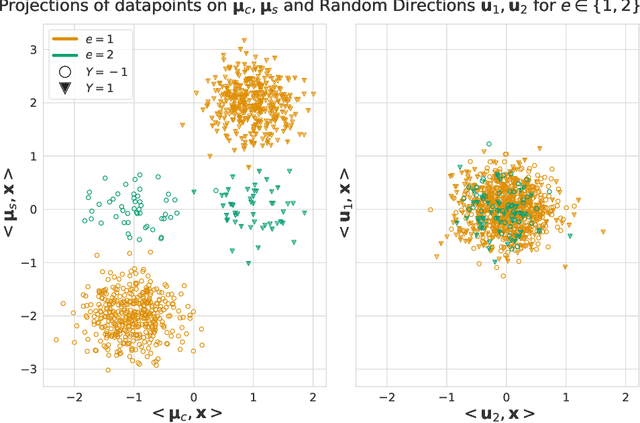
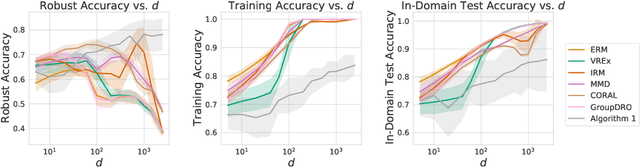
Learned classifiers should often possess certain invariance properties meant to encourage fairness, robustness, or out-of-distribution generalization. However, multiple recent works empirically demonstrate that common invariance-inducing regularizers are ineffective in the over-parameterized regime, in which classifiers perfectly fit (i.e. interpolate) the training data. This suggests that the phenomenon of ``benign overfitting," in which models generalize well despite interpolating, might not favorably extend to settings in which robustness or fairness are desirable. In this work we provide a theoretical justification for these observations. We prove that -- even in the simplest of settings -- any interpolating learning rule (with arbitrarily small margin) will not satisfy these invariance properties. We then propose and analyze an algorithm that -- in the same setting -- successfully learns a non-interpolating classifier that is provably invariant. We validate our theoretical observations on simulated data and the Waterbirds dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge