The Fragility of Fairness: Causal Sensitivity Analysis for Fair Machine Learning

Fairness metrics are a core tool in the fair machine learning literature (FairML), used to determine that ML models are, in some sense, "fair". Real-world data, however, are typically plagued by various measurement biases and other violated assumptions, which can render fairness assessments meaningless. We adapt tools from causal sensitivity analysis to the FairML context, providing a general framework which (1) accommodates effectively any combination of fairness metric and bias that can be posed in the "oblivious setting"; (2) allows researchers to investigate combinations of biases, resulting in non-linear sensitivity; and (3) enables flexible encoding of domain-specific constraints and assumptions. Employing this framework, we analyze the sensitivity of the most common parity metrics under 3 varieties of classifier across 14 canonical fairness datasets. Our analysis reveals the striking fragility of fairness assessments to even minor dataset biases. We show that causal sensitivity analysis provides a powerful and necessary toolkit for gauging the informativeness of parity metric evaluations. Our repository is available here: https://github.com/Jakefawkes/fragile_fair.

Is merging worth it? Securely evaluating the information gain for causal dataset acquisition

Merging datasets across institutions is a lengthy and costly procedure, especially when it involves private information. Data hosts may therefore want to prospectively gauge which datasets are most beneficial to merge with, without revealing sensitive information. For causal estimation this is particularly challenging as the value of a merge will depend not only on the reduction in epistemic uncertainty but also the improvement in overlap. To address this challenge, we introduce the first cryptographically secure information-theoretic approach for quantifying the value of a merge in the context of heterogeneous treatment effect estimation. We do this by evaluating the Expected Information Gain (EIG) and utilising multi-party computation to ensure it can be securely computed without revealing any raw data. As we demonstrate, this can be used with differential privacy (DP) to ensure privacy requirements whilst preserving more accurate computation than naive DP alone. To the best of our knowledge, this work presents the first privacy-preserving method for dataset acquisition tailored to causal estimation. We demonstrate the effectiveness and reliability of our method on a range of simulated and realistic benchmarks. The code is available anonymously.

The Role of Learning Algorithms in Collective Action

Collective action in Machine Learning is the study of the control that a coordinated group can have over machine learning algorithms. While previous research has concentrated on assessing the impact of collectives against Bayes optimal classifiers, this perspective is limited, given that in reality, classifiers seldom achieve Bayes optimality and are influenced by the choice of learning algorithms along with their inherent inductive biases. In this work, we initiate the study of how the choice of the learning algorithm plays a role in the success of a collective in practical settings. Specifically, we focus on distributionally robust algorithms (DRO), popular for improving a worst group error, and on the popular stochastic gradient descent (SGD), due to its inductive bias for "simpler" functions. Our empirical results, supported by a theoretical foundation, show that the effective size and success of the collective are highly dependent on properties of the learning algorithm. This highlights the necessity of taking the learning algorithm into account when studying the impact of collective action in Machine learning.

Results on Counterfactual Invariance

In this paper we provide a theoretical analysis of counterfactual invariance. We present a variety of existing definitions, study how they relate to each other and what their graphical implications are. We then turn to the current major question surrounding counterfactual invariance, how does it relate to conditional independence? We show that whilst counterfactual invariance implies conditional independence, conditional independence does not give any implications about the degree or likelihood of satisfying counterfactual invariance. Furthermore, we show that for discrete causal models counterfactually invariant functions are often constrained to be functions of particular variables, or even constant.

Returning The Favour: When Regression Benefits From Probabilistic Causal Knowledge

A directed acyclic graph (DAG) provides valuable prior knowledge that is often discarded in regression tasks in machine learning. We show that the independences arising from the presence of collider structures in DAGs provide meaningful inductive biases, which constrain the regression hypothesis space and improve predictive performance. We introduce collider regression, a framework to incorporate probabilistic causal knowledge from a collider in a regression problem. When the hypothesis space is a reproducing kernel Hilbert space, we prove a strictly positive generalisation benefit under mild assumptions and provide closed-form estimators of the empirical risk minimiser. Experiments on synthetic and climate model data demonstrate performance gains of the proposed methodology.

Doubly Robust Kernel Statistics for Testing Distributional Treatment Effects Even Under One Sided Overlap

As causal inference becomes more widespread the importance of having good tools to test for causal effects increases. In this work we focus on the problem of testing for causal effects that manifest in a difference in distribution for treatment and control. We build on work applying kernel methods to causality, considering the previously introduced Counterfactual Mean Embedding framework (\textsc{CfME}). We improve on this by proposing the \emph{Doubly Robust Counterfactual Mean Embedding} (\textsc{DR-CfME}), which has better theoretical properties than its predecessor by leveraging semiparametric theory. This leads us to propose new kernel based test statistics for distributional effects which are based upon doubly robust estimators of treatment effects. We propose two test statistics, one which is a direct improvement on previous work and one which can be applied even when the support of the treatment arm is a subset of that of the control arm. We demonstrate the validity of our methods on simulated and real-world data, as well as giving an application in off-policy evaluation.

Selection, Ignorability and Challenges With Causal Fairness

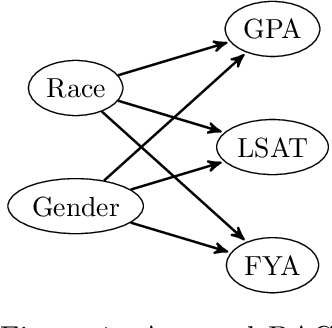
In this paper we look at popular fairness methods that use causal counterfactuals. These methods capture the intuitive notion that a prediction is fair if it coincides with the prediction that would have been made if someone's race, gender or religion were counterfactually different. In order to achieve this, we must have causal models that are able to capture what someone would be like if we were to counterfactually change these traits. However, we argue that any model that can do this must lie outside the particularly well behaved class that is commonly considered in the fairness literature. This is because in fairness settings, models in this class entail a particularly strong causal assumption, normally only seen in a randomised controlled trial. We argue that in general this is unlikely to hold. Furthermore, we show in many cases it can be explicitly rejected due to the fact that samples are selected from a wider population. We show this creates difficulties for counterfactual fairness as well as for the application of more general causal fairness methods.