Squared families: Searching beyond regular probability models

We introduce squared families, which are families of probability densities obtained by squaring a linear transformation of a statistic. Squared families are singular, however their singularity can easily be handled so that they form regular models. After handling the singularity, squared families possess many convenient properties. Their Fisher information is a conformal transformation of the Hessian metric induced from a Bregman generator. The Bregman generator is the normalising constant, and yields a statistical divergence on the family. The normalising constant admits a helpful parameter-integral factorisation, meaning that only one parameter-independent integral needs to be computed for all normalising constants in the family, unlike in exponential families. Finally, the squared family kernel is the only integral that needs to be computed for the Fisher information, statistical divergence and normalising constant. We then describe how squared families are special in the broader class of $g$-families, which are obtained by applying a sufficiently regular function $g$ to a linear transformation of a statistic. After removing special singularities, positively homogeneous families and exponential families are the only $g$-families for which the Fisher information is a conformal transformation of the Hessian metric, where the generator depends on the parameter only through the normalising constant. Even-order monomial families also admit parameter-integral factorisations, unlike exponential families. We study parameter estimation and density estimation in squared families, in the well-specified and misspecified settings. We use a universal approximation property to show that squared families can learn sufficiently well-behaved target densities at a rate of $\mathcal{O}(N^{-1/2})+C n^{-1/4}$, where $N$ is the number of datapoints, $n$ is the number of parameters, and $C$ is some constant.

Near-Optimal Approximations for Bayesian Inference in Function Space

We propose a scalable inference algorithm for Bayes posteriors defined on a reproducing kernel Hilbert space (RKHS). Given a likelihood function and a Gaussian random element representing the prior, the corresponding Bayes posterior measure $\Pi_{\text{B}}$ can be obtained as the stationary distribution of an RKHS-valued Langevin diffusion. We approximate the infinite-dimensional Langevin diffusion via a projection onto the first $M$ components of the Kosambi-Karhunen-Lo\`eve expansion. Exploiting the thus obtained approximate posterior for these $M$ components, we perform inference for $\Pi_{\text{B}}$ by relying on the law of total probability and a sufficiency assumption. The resulting method scales as $O(M^3+JM^2)$, where $J$ is the number of samples produced from the posterior measure $\Pi_{\text{B}}$. Interestingly, the algorithm recovers the posterior arising from the sparse variational Gaussian process (SVGP) (see Titsias, 2009) as a special case, owed to the fact that the sufficiency assumption underlies both methods. However, whereas the SVGP is parametrically constrained to be a Gaussian process, our method is based on a non-parametric variational family $\mathcal{P}(\mathbb{R}^M)$ consisting of all probability measures on $\mathbb{R}^M$. As a result, our method is provably close to the optimal $M$-dimensional variational approximation of the Bayes posterior $\Pi_{\text{B}}$ in $\mathcal{P}(\mathbb{R}^M)$ for convex and Lipschitz continuous negative log likelihoods, and coincides with SVGP for the special case of a Gaussian error likelihood.

All Models Are Miscalibrated, But Some Less So: Comparing Calibration with Conditional Mean Operators

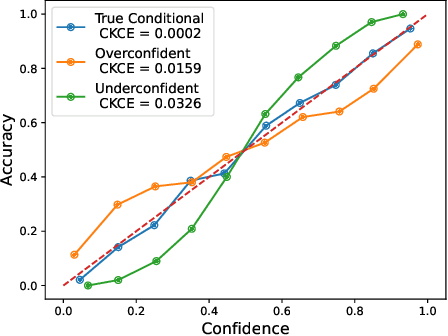
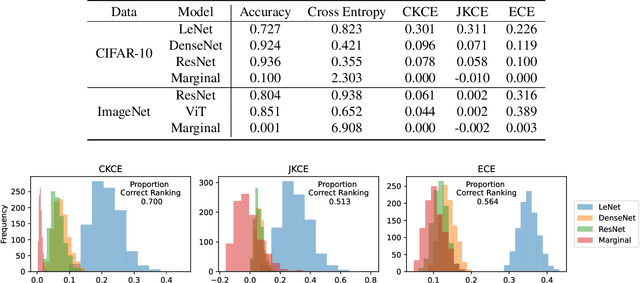
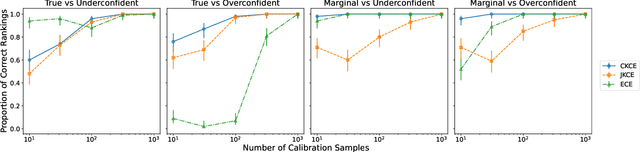
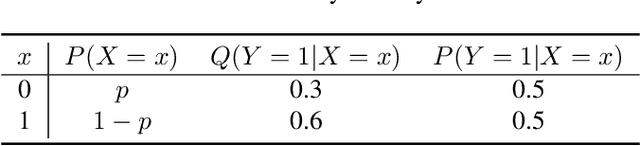
When working in a high-risk setting, having well calibrated probabilistic predictive models is a crucial requirement. However, estimators for calibration error are not always able to correctly distinguish which model is better calibrated. We propose the \emph{conditional kernel calibration error} (CKCE) which is based on the Hilbert-Schmidt norm of the difference between conditional mean operators. By working directly with the definition of strong calibration as the distance between conditional distributions, which we represent by their embeddings in reproducing kernel Hilbert spaces, the CKCE is less sensitive to the marginal distribution of predictive models. This makes it more effective for relative comparisons than previously proposed calibration metrics. Our experiments, using both synthetic and real data, show that CKCE provides a more consistent ranking of models by their calibration error and is more robust against distribution shift.

Indirect Query Bayesian Optimization with Integrated Feedback

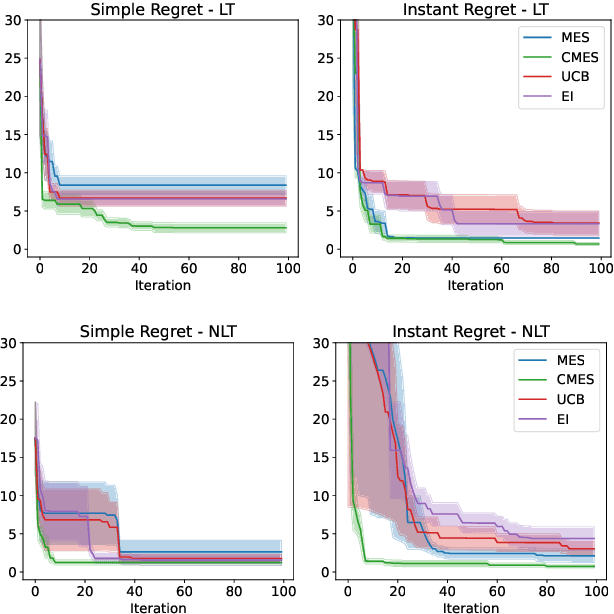
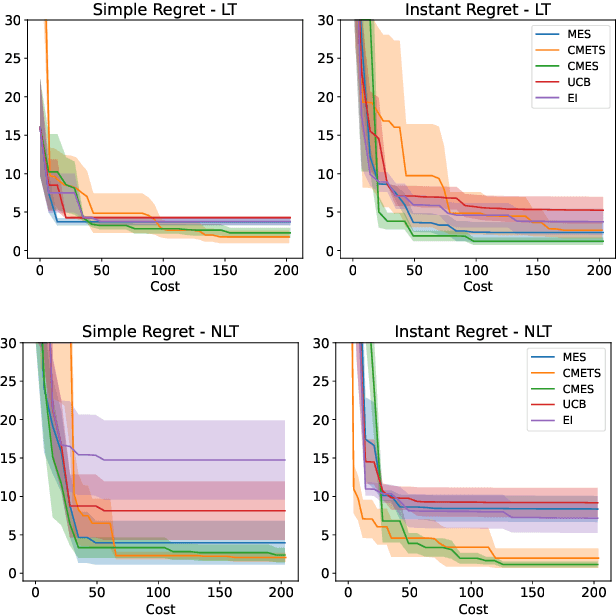
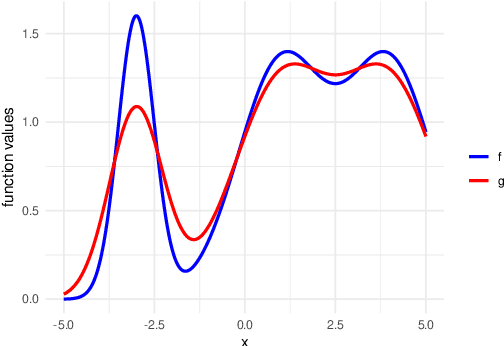
We develop the framework of Indirect Query Bayesian Optimization (IQBO), a new class of Bayesian optimization problems where the integrated feedback is given via a conditional expectation of the unknown function $f$ to be optimized. The underlying conditional distribution can be unknown and learned from data. The goal is to find the global optimum of $f$ by adaptively querying and observing in the space transformed by the conditional distribution. This is motivated by real-world applications where one cannot access direct feedback due to privacy, hardware or computational constraints. We propose the Conditional Max-Value Entropy Search (CMES) acquisition function to address this novel setting, and propose a hierarchical search algorithm to address the multi-resolution setting and improve the computational efficiency. We show regret bounds for our proposed methods and demonstrate the effectiveness of our approaches on simulated optimization tasks.

Label Distribution Learning using the Squared Neural Family on the Probability Simplex

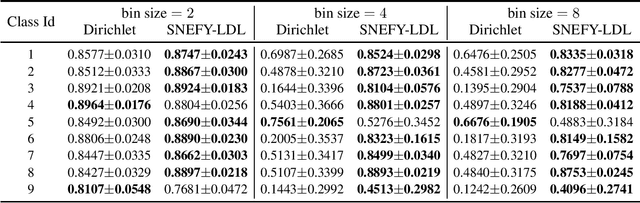
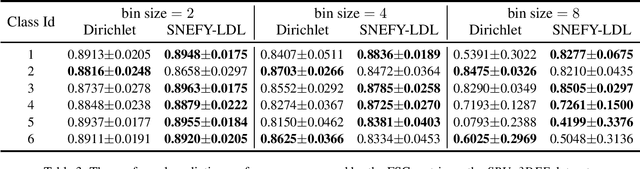
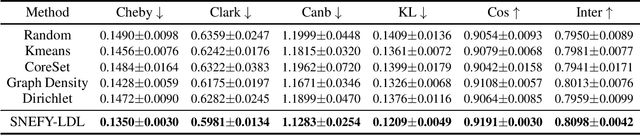
Label distribution learning (LDL) provides a framework wherein a distribution over categories rather than a single category is predicted, with the aim of addressing ambiguity in labeled data. Existing research on LDL mainly focuses on the task of point estimation, i.e., pinpointing an optimal distribution in the probability simplex conditioned on the input sample. In this paper, we estimate a probability distribution of all possible label distributions over the simplex, by unleashing the expressive power of the recently introduced Squared Neural Family (SNEFY). With the modeled distribution, label distribution prediction can be achieved by performing the expectation operation to estimate the mean of the distribution of label distributions. Moreover, more information about the label distribution can be inferred, such as the prediction reliability and uncertainties. We conduct extensive experiments on the label distribution prediction task, showing that our distribution modeling based method can achieve very competitive label distribution prediction performance compared with the state-of-the-art baselines. Additional experiments on active learning and ensemble learning demonstrate that our probabilistic approach can effectively boost the performance in these settings, by accurately estimating the prediction reliability and uncertainties.

An Overview of Causal Inference using Kernel Embeddings

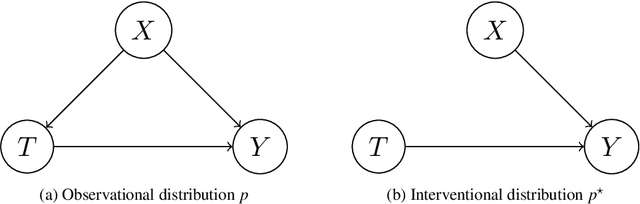
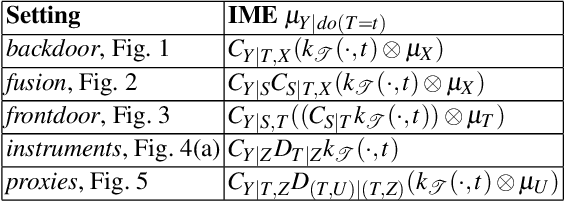
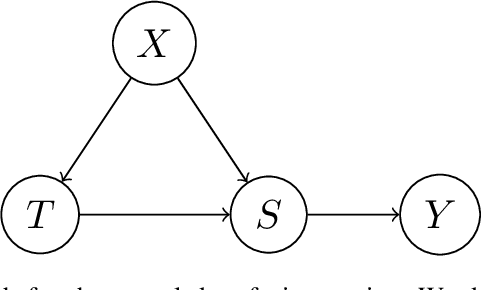
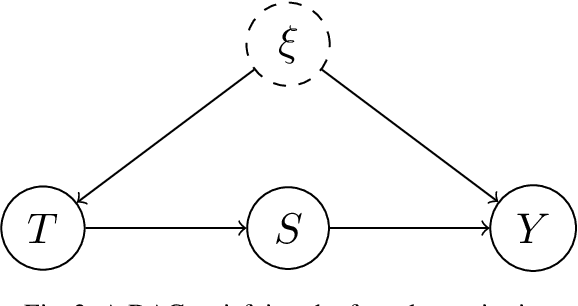
Kernel embeddings have emerged as a powerful tool for representing probability measures in a variety of statistical inference problems. By mapping probability measures into a reproducing kernel Hilbert space (RKHS), kernel embeddings enable flexible representations of complex relationships between variables. They serve as a mechanism for efficiently transferring the representation of a distribution downstream to other tasks, such as hypothesis testing or causal effect estimation. In the context of causal inference, the main challenges include identifying causal associations and estimating the average treatment effect from observational data, where confounding variables may obscure direct cause-and-effect relationships. Kernel embeddings provide a robust nonparametric framework for addressing these challenges. They allow for the representations of distributions of observational data and their seamless transformation into representations of interventional distributions to estimate relevant causal quantities. We overview recent research that leverages the expressiveness of kernel embeddings in tandem with causal inference.

Credal Two-Sample Tests of Epistemic Ignorance

We introduce credal two-sample testing, a new hypothesis testing framework for comparing credal sets -- convex sets of probability measures where each element captures aleatoric uncertainty and the set itself represents epistemic uncertainty that arises from the modeller's partial ignorance. Classical two-sample tests, which rely on comparing precise distributions, fail to address epistemic uncertainty due to partial ignorance. To bridge this gap, we generalise two-sample tests to compare credal sets, enabling reasoning for equality, inclusion, intersection, and mutual exclusivity, each offering unique insights into the modeller's epistemic beliefs. We formalise these tests as two-sample tests with nuisance parameters and introduce the first permutation-based solution for this class of problems, significantly improving upon existing methods. Our approach properly incorporates the modeller's epistemic uncertainty into hypothesis testing, leading to more robust and credible conclusions, with kernel-based implementations for real-world applications.

Bayesian Low-Rank LeArning (Bella): A Practical Approach to Bayesian Neural Networks

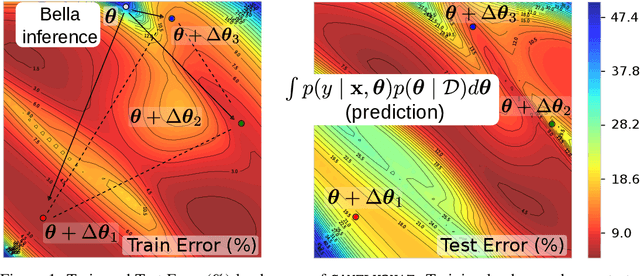
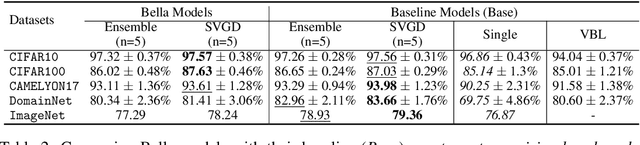
Computational complexity of Bayesian learning is impeding its adoption in practical, large-scale tasks. Despite demonstrations of significant merits such as improved robustness and resilience to unseen or out-of-distribution inputs over their non- Bayesian counterparts, their practical use has faded to near insignificance. In this study, we introduce an innovative framework to mitigate the computational burden of Bayesian neural networks (BNNs). Our approach follows the principle of Bayesian techniques based on deep ensembles, but significantly reduces their cost via multiple low-rank perturbations of parameters arising from a pre-trained neural network. Both vanilla version of ensembles as well as more sophisticated schemes such as Bayesian learning with Stein Variational Gradient Descent (SVGD), previously deemed impractical for large models, can be seamlessly implemented within the proposed framework, called Bayesian Low-Rank LeArning (Bella). In a nutshell, i) Bella achieves a dramatic reduction in the number of trainable parameters required to approximate a Bayesian posterior; and ii) it not only maintains, but in some instances, surpasses the performance of conventional Bayesian learning methods and non-Bayesian baselines. Our results with large-scale tasks such as ImageNet, CAMELYON17, DomainNet, VQA with CLIP, LLaVA demonstrate the effectiveness and versatility of Bella in building highly scalable and practical Bayesian deep models for real-world applications.

Bayesian Adaptive Calibration and Optimal Design

The process of calibrating computer models of natural phenomena is essential for applications in the physical sciences, where plenty of domain knowledge can be embedded into simulations and then calibrated against real observations. Current machine learning approaches, however, mostly rely on rerunning simulations over a fixed set of designs available in the observed data, potentially neglecting informative correlations across the design space and requiring a large amount of simulations. Instead, we consider the calibration process from the perspective of Bayesian adaptive experimental design and propose a data-efficient algorithm to run maximally informative simulations within a batch-sequential process. At each round, the algorithm jointly estimates the parameters of the posterior distribution and optimal designs by maximising a variational lower bound of the expected information gain. The simulator is modelled as a sample from a Gaussian process, which allows us to correlate simulations and observed data with the unknown calibration parameters. We show the benefits of our method when compared to related approaches across synthetic and real-data problems.

Neural-Kernel Conditional Mean Embeddings

Kernel conditional mean embeddings (CMEs) offer a powerful framework for representing conditional distribution, but they often face scalability and expressiveness challenges. In this work, we propose a new method that effectively combines the strengths of deep learning with CMEs in order to address these challenges. Specifically, our approach leverages the end-to-end neural network (NN) optimization framework using a kernel-based objective. This design circumvents the computationally expensive Gram matrix inversion required by current CME methods. To further enhance performance, we provide efficient strategies to optimize the remaining kernel hyperparameters. In conditional density estimation tasks, our NN-CME hybrid achieves competitive performance and often surpasses existing deep learning-based methods. Lastly, we showcase its remarkable versatility by seamlessly integrating it into reinforcement learning (RL) contexts. Building on Q-learning, our approach naturally leads to a new variant of distributional RL methods, which demonstrates consistent effectiveness across different environments.