Bayesian Adaptive Calibration and Optimal Design

The process of calibrating computer models of natural phenomena is essential for applications in the physical sciences, where plenty of domain knowledge can be embedded into simulations and then calibrated against real observations. Current machine learning approaches, however, mostly rely on rerunning simulations over a fixed set of designs available in the observed data, potentially neglecting informative correlations across the design space and requiring a large amount of simulations. Instead, we consider the calibration process from the perspective of Bayesian adaptive experimental design and propose a data-efficient algorithm to run maximally informative simulations within a batch-sequential process. At each round, the algorithm jointly estimates the parameters of the posterior distribution and optimal designs by maximising a variational lower bound of the expected information gain. The simulator is modelled as a sample from a Gaussian process, which allows us to correlate simulations and observed data with the unknown calibration parameters. We show the benefits of our method when compared to related approaches across synthetic and real-data problems.

Cross-Entropy Estimators for Sequential Experiment Design with Reinforcement Learning

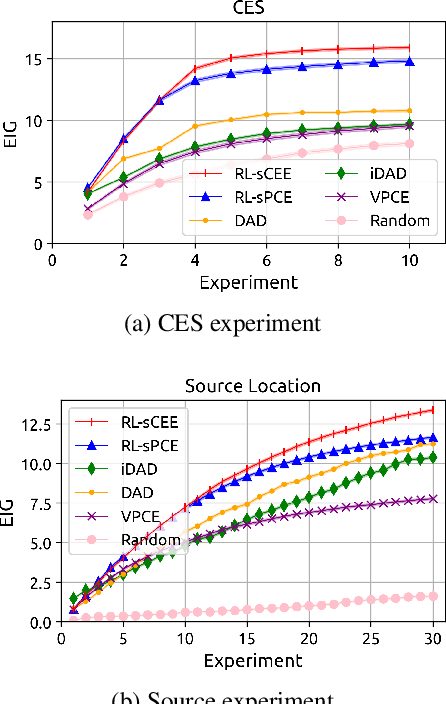
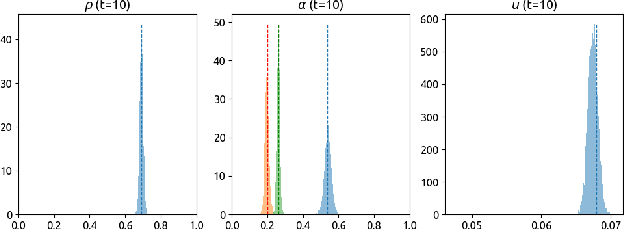
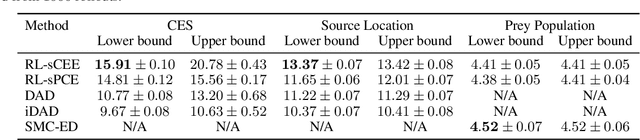
Reinforcement learning can effectively learn amortised design policies for designing sequences of experiments. However, current methods rely on contrastive estimators of expected information gain, which require an exponential number of contrastive samples to achieve an unbiased estimation. We propose an alternative lower bound estimator, based on the cross-entropy of the joint model distribution and a flexible proposal distribution. This proposal distribution approximates the true posterior of the model parameters given the experimental history and the design policy. Our estimator requires no contrastive samples, can achieve more accurate estimates of high information gains, allows learning of superior design policies, and is compatible with implicit probabilistic models. We assess our algorithm's performance in various tasks, including continuous and discrete designs and explicit and implicit likelihoods.

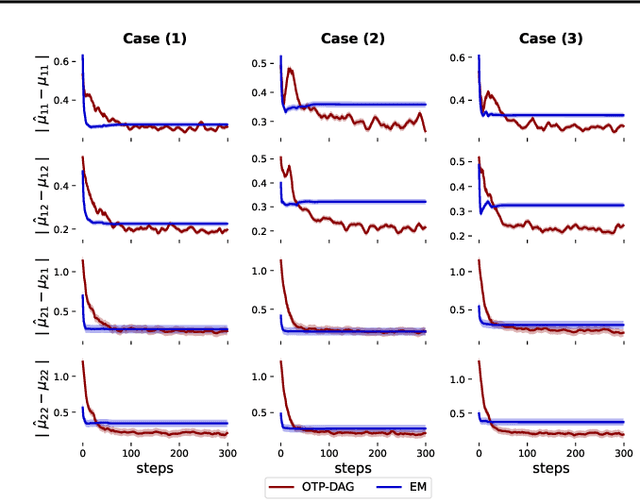
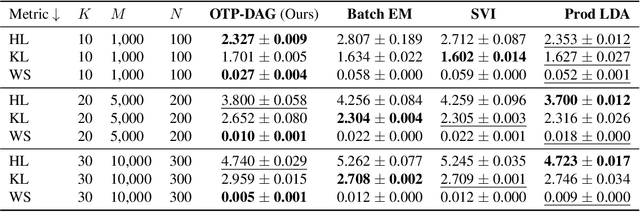
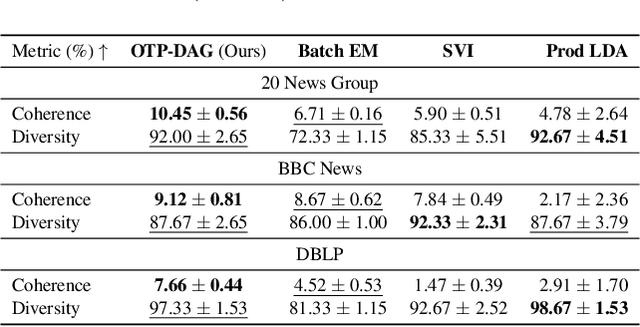
Learning Directed Graphical Models with Optimal Transport

Estimating the parameters of a probabilistic directed graphical model from incomplete data remains a long-standing challenge. This is because, in the presence of latent variables, both the likelihood function and posterior distribution are intractable without further assumptions about structural dependencies or model classes. While existing learning methods are fundamentally based on likelihood maximization, here we offer a new view of the parameter learning problem through the lens of optimal transport. This perspective licenses a framework that operates on many directed graphs without making unrealistic assumptions on the posterior over the latent variables or resorting to black-box variational approximations. We develop a theoretical framework and support it with extensive empirical evidence demonstrating the flexibility and versatility of our approach. Across experiments, we show that not only can our method recover the ground-truth parameters but it also performs competitively on downstream applications, notably the non-trivial task of discrete representation learning.

Transformed Distribution Matching for Missing Value Imputation

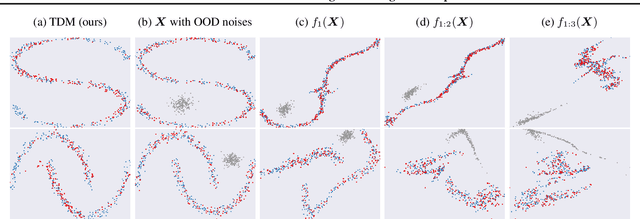
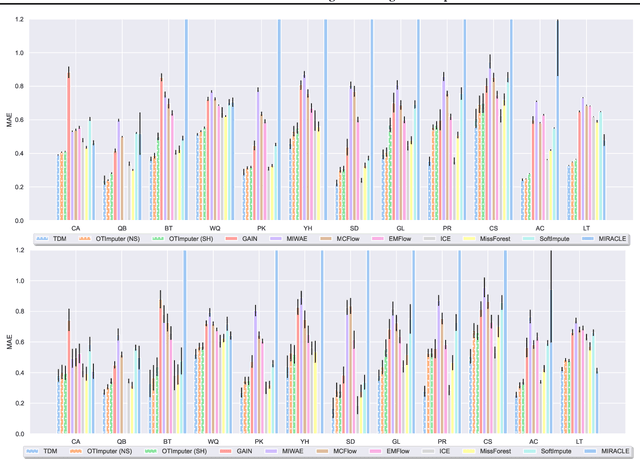
We study the problem of imputing missing values in a dataset, which has important applications in many domains. The key to missing value imputation is to capture the data distribution with incomplete samples and impute the missing values accordingly. In this paper, by leveraging the fact that any two batches of data with missing values come from the same data distribution, we propose to impute the missing values of two batches of samples by transforming them into a latent space through deep invertible functions and matching them distributionally. To learn the transformations and impute the missing values simultaneously, a simple and well-motivated algorithm is proposed. Extensive experiments over a large number of datasets and competing benchmark algorithms show that our method achieves state-of-the-art performance.

Learning to Counter: Stochastic Feature-based Learning for Diverse Counterfactual Explanations

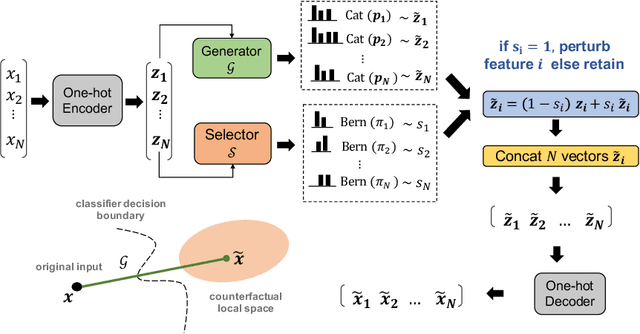
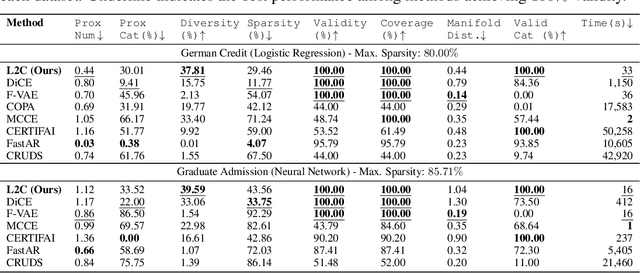
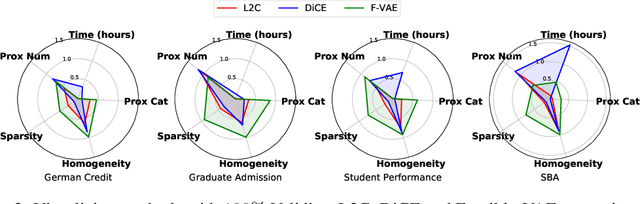
Interpretable machine learning seeks to understand the reasoning process of complex black-box systems that are long notorious for lack of explainability. One growing interpreting approach is through counterfactual explanations, which go beyond why a system arrives at a certain decision to further provide suggestions on what a user can do to alter the outcome. A counterfactual example must be able to counter the original prediction from the black-box classifier, while also satisfying various constraints for practical applications. These constraints exist at trade-offs between one and another presenting radical challenges to existing works. To this end, we propose a stochastic learning-based framework that effectively balances the counterfactual trade-offs. The framework consists of a generation and a feature selection module with complementary roles: the former aims to model the distribution of valid counterfactuals whereas the latter serves to enforce additional constraints in a way that allows for differentiable training and amortized optimization. We demonstrate the effectiveness of our method in generating actionable and plausible counterfactuals that are more diverse than the existing methods and particularly in a more efficient manner than counterparts of the same capacity.

Optimizing Sequential Experimental Design with Deep Reinforcement Learning

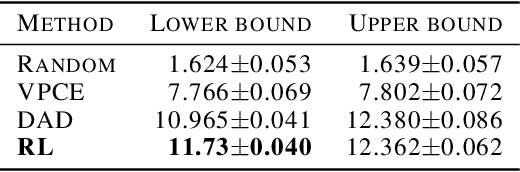
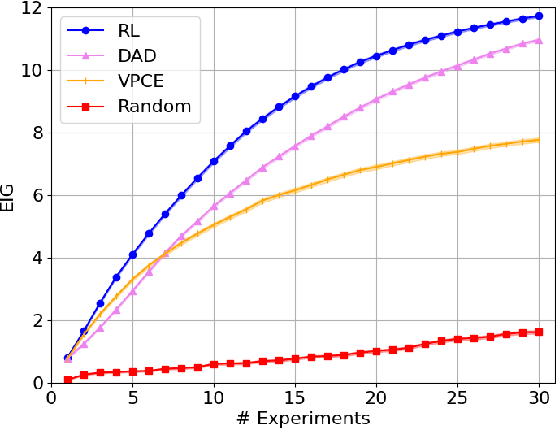
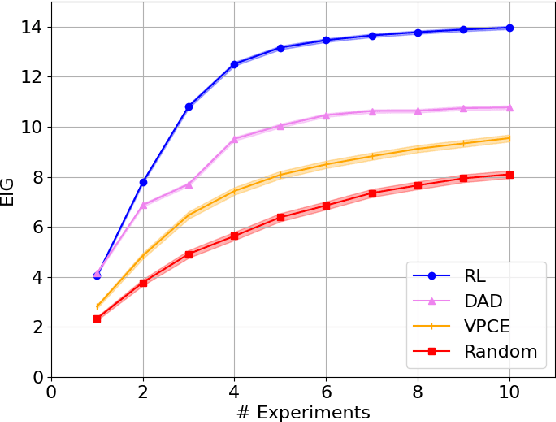
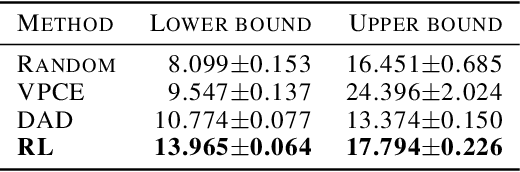
Bayesian approaches developed to solve the optimal design of sequential experiments are mathematically elegant but computationally challenging. Recently, techniques using amortization have been proposed to make these Bayesian approaches practical, by training a parameterized policy that proposes designs efficiently at deployment time. However, these methods may not sufficiently explore the design space, require access to a differentiable probabilistic model and can only optimize over continuous design spaces. Here, we address these limitations by showing that the problem of optimizing policies can be reduced to solving a Markov decision process (MDP). We solve the equivalent MDP with modern deep reinforcement learning techniques. Our experiments show that our approach is also computationally efficient at deployment time and exhibits state-of-the-art performance on both continuous and discrete design spaces, even when the probabilistic model is a black box.

Log Gaussian Cox Process Networks

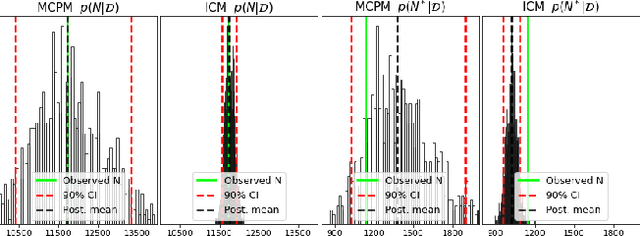
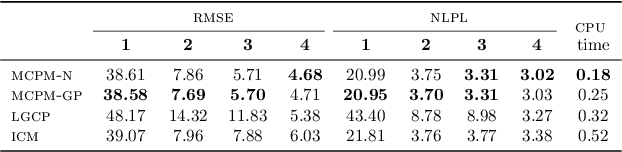
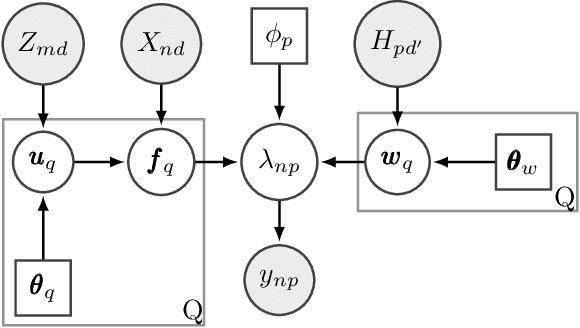
We generalize the log Gaussian Cox process (LGCP) framework to model multiple correlated point data jointly. The resulting log Gaussian Cox process network (LGCPN) considers the observations as realizations of multiple LGCPs, whose log intensities are given by linear combinations of latent functions drawn from Gaussian process priors. The coefficients of these linear combinations are also drawn from Gaussian processes and can incorporate additional dependencies a priori. We derive closed-form expressions for the moments of the intensity functions in our model and use them to develop an efficient variational inference algorithm that is orders of magnitude faster than competing deterministic and stochastic approximations of multivariate LGCP and coregionalization models. Our approach outperforms the state of the art in jointly estimating multiple bovine tuberculosis incidents in Cornwall, UK, and multiple crime type intensities across New York city.

Discriminative Probabilistic Prototype Learning

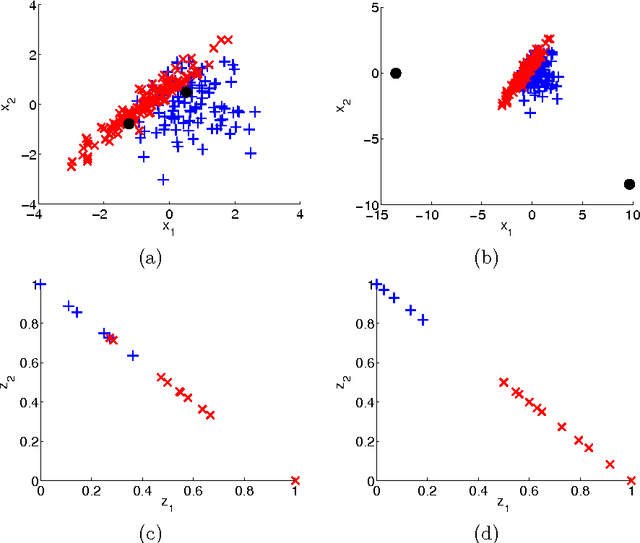
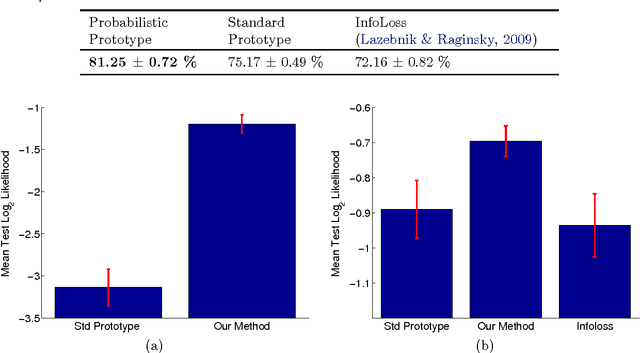
In this paper we propose a simple yet powerful method for learning representations in supervised learning scenarios where each original input datapoint is described by a set of vectors and their associated outputs may be given by soft labels indicating, for example, class probabilities. We represent an input datapoint as a mixture of probabilities over the corresponding set of feature vectors where each probability indicates how likely each vector is to belong to an unknown prototype pattern. We propose a probabilistic model that parameterizes these prototype patterns in terms of hidden variables and therefore it can be trained with conventional approaches based on likelihood maximization. More importantly, both the model parameters and the prototype patterns can be learned from data in a discriminative way. We show that our model can be seen as a probabilistic generalization of learning vector quantization (LVQ). We apply our method to the problems of shape classification, hyperspectral imaging classification and people's work class categorization, showing the superior performance of our method compared to the standard prototype-based classification approach and other competitive benchmark methods.