BIG-Bench Extra Hard

Large language models (LLMs) are increasingly deployed in everyday applications, demanding robust general reasoning capabilities and diverse reasoning skillset. However, current LLM reasoning benchmarks predominantly focus on mathematical and coding abilities, leaving a gap in evaluating broader reasoning proficiencies. One particular exception is the BIG-Bench dataset, which has served as a crucial benchmark for evaluating the general reasoning capabilities of LLMs, thanks to its diverse set of challenging tasks that allowed for a comprehensive assessment of general reasoning across various skills within a unified framework. However, recent advances in LLMs have led to saturation on BIG-Bench, and its harder version BIG-Bench Hard (BBH). State-of-the-art models achieve near-perfect scores on many tasks in BBH, thus diminishing its utility. To address this limitation, we introduce BIG-Bench Extra Hard (BBEH), a new benchmark designed to push the boundaries of LLM reasoning evaluation. BBEH replaces each task in BBH with a novel task that probes a similar reasoning capability but exhibits significantly increased difficulty. We evaluate various models on BBEH and observe a (harmonic) average accuracy of 9.8\% for the best general-purpose model and 44.8\% for the best reasoning-specialized model, indicating substantial room for improvement and highlighting the ongoing challenge of achieving robust general reasoning in LLMs. We release BBEH publicly at: https://github.com/google-deepmind/bbeh.

Prompting Strategies for Enabling Large Language Models to Infer Causation from Correlation

The reasoning abilities of Large Language Models (LLMs) are attracting increasing attention. In this work, we focus on causal reasoning and address the task of establishing causal relationships based on correlation information, a highly challenging problem on which several LLMs have shown poor performance. We introduce a prompting strategy for this problem that breaks the original task into fixed subquestions, with each subquestion corresponding to one step of a formal causal discovery algorithm, the PC algorithm. The proposed prompting strategy, PC-SubQ, guides the LLM to follow these algorithmic steps, by sequentially prompting it with one subquestion at a time, augmenting the next subquestion's prompt with the answer to the previous one(s). We evaluate our approach on an existing causal benchmark, Corr2Cause: our experiments indicate a performance improvement across five LLMs when comparing PC-SubQ to baseline prompting strategies. Results are robust to causal query perturbations, when modifying the variable names or paraphrasing the expressions.

GradINN: Gradient Informed Neural Network

We propose Gradient Informed Neural Networks (GradINNs), a methodology inspired by Physics Informed Neural Networks (PINNs) that can be used to efficiently approximate a wide range of physical systems for which the underlying governing equations are completely unknown or cannot be defined, a condition that is often met in complex engineering problems. GradINNs leverage prior beliefs about a system's gradient to constrain the predicted function's gradient across all input dimensions. This is achieved using two neural networks: one modeling the target function and an auxiliary network expressing prior beliefs, e.g., smoothness. A customized loss function enables training the first network while enforcing gradient constraints derived from the auxiliary network. We demonstrate the advantages of GradINNs, particularly in low-data regimes, on diverse problems spanning non time-dependent systems (Friedman function, Stokes Flow) and time-dependent systems (Lotka-Volterra, Burger's equation). Experimental results showcase strong performance compared to standard neural networks and PINN-like approaches across all tested scenarios.

FunBO: Discovering Acquisition Functions for Bayesian Optimization with FunSearch

The sample efficiency of Bayesian optimization algorithms depends on carefully crafted acquisition functions (AFs) guiding the sequential collection of function evaluations. The best-performing AF can vary significantly across optimization problems, often requiring ad-hoc and problem-specific choices. This work tackles the challenge of designing novel AFs that perform well across a variety of experimental settings. Based on FunSearch, a recent work using Large Language Models (LLMs) for discovery in mathematical sciences, we propose FunBO, an LLM-based method that can be used to learn new AFs written in computer code by leveraging access to a limited number of evaluations for a set of objective functions. We provide the analytic expression of all discovered AFs and evaluate them on various global optimization benchmarks and hyperparameter optimization tasks. We show how FunBO identifies AFs that generalize well in and out of the training distribution of functions, thus outperforming established general-purpose AFs and achieving competitive performance against AFs that are customized to specific function types and are learned via transfer-learning algorithms.

Additive Causal Bandits with Unknown Graph

We explore algorithms to select actions in the causal bandit setting where the learner can choose to intervene on a set of random variables related by a causal graph, and the learner sequentially chooses interventions and observes a sample from the interventional distribution. The learner's goal is to quickly find the intervention, among all interventions on observable variables, that maximizes the expectation of an outcome variable. We depart from previous literature by assuming no knowledge of the causal graph except that latent confounders between the outcome and its ancestors are not present. We first show that the unknown graph problem can be exponentially hard in the parents of the outcome. To remedy this, we adopt an additional additive assumption on the outcome which allows us to solve the problem by casting it as an additive combinatorial linear bandit problem with full-bandit feedback. We propose a novel action-elimination algorithm for this setting, show how to apply this algorithm to the causal bandit problem, provide sample complexity bounds, and empirically validate our findings on a suite of randomly generated causal models, effectively showing that one does not need to explicitly learn the parents of the outcome to identify the best intervention.

Functional Causal Bayesian Optimization

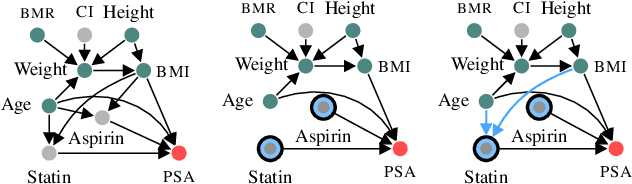
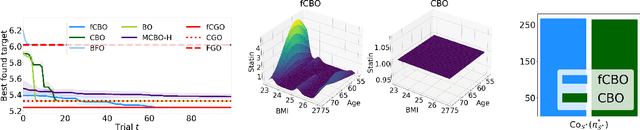
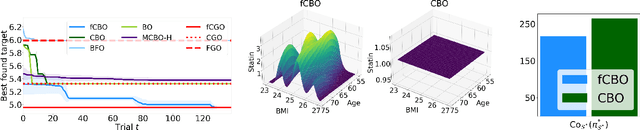
We propose functional causal Bayesian optimization (fCBO), a method for finding interventions that optimize a target variable in a known causal graph. fCBO extends the CBO family of methods to enable functional interventions, which set a variable to be a deterministic function of other variables in the graph. fCBO models the unknown objectives with Gaussian processes whose inputs are defined in a reproducing kernel Hilbert space, thus allowing to compute distances among vector-valued functions. In turn, this enables to sequentially select functions to explore by maximizing an expected improvement acquisition functional while keeping the typical computational tractability of standard BO settings. We introduce graphical criteria that establish when considering functional interventions allows attaining better target effects, and conditions under which selected interventions are also optimal for conditional target effects. We demonstrate the benefits of the method in a synthetic and in a real-world causal graph.

Constrained Causal Bayesian Optimization

We propose constrained causal Bayesian optimization (cCBO), an approach for finding interventions in a known causal graph that optimize a target variable under some constraints. cCBO first reduces the search space by exploiting the graph structure and, if available, an observational dataset; and then solves the restricted optimization problem by modelling target and constraint quantities using Gaussian processes and by sequentially selecting interventions via a constrained expected improvement acquisition function. We propose different surrogate models that enable to integrate observational and interventional data while capturing correlation among effects with increasing levels of sophistication. We evaluate cCBO on artificial and real-world causal graphs showing successful trade off between fast convergence and percentage of feasible interventions.

Causal Entropy Optimization

We study the problem of globally optimizing the causal effect on a target variable of an unknown causal graph in which interventions can be performed. This problem arises in many areas of science including biology, operations research and healthcare. We propose Causal Entropy Optimization (CEO), a framework that generalizes Causal Bayesian Optimization (CBO) to account for all sources of uncertainty, including the one arising from the causal graph structure. CEO incorporates the causal structure uncertainty both in the surrogate models for the causal effects and in the mechanism used to select interventions via an information-theoretic acquisition function. The resulting algorithm automatically trades-off structure learning and causal effect optimization, while naturally accounting for observation noise. For various synthetic and real-world structural causal models, CEO achieves faster convergence to the global optimum compared with CBO while also learning the graph. Furthermore, our joint approach to structure learning and causal optimization improves upon sequential, structure-learning-first approaches.

Dynamic Causal Bayesian Optimization

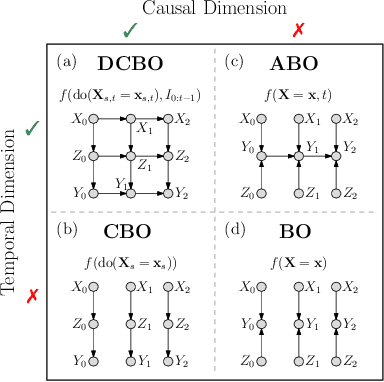
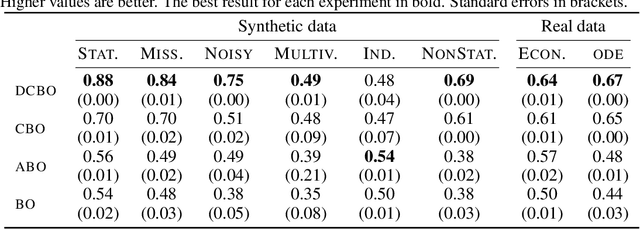
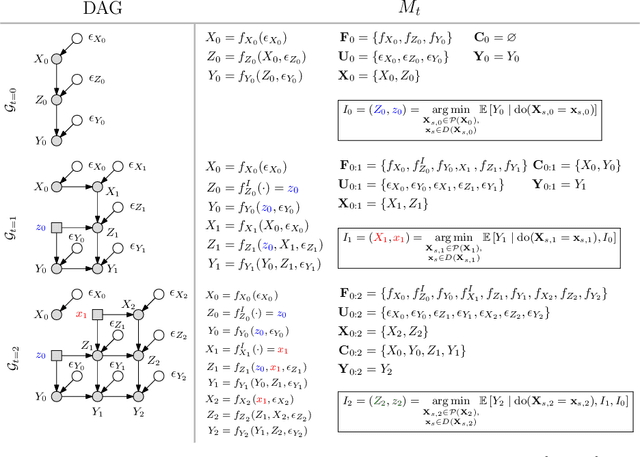
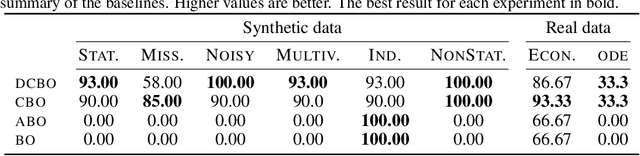
This paper studies the problem of performing a sequence of optimal interventions in a causal dynamical system where both the target variable of interest and the inputs evolve over time. This problem arises in a variety of domains e.g. system biology and operational research. Dynamic Causal Bayesian Optimization (DCBO) brings together ideas from sequential decision making, causal inference and Gaussian process (GP) emulation. DCBO is useful in scenarios where all causal effects in a graph are changing over time. At every time step DCBO identifies a local optimal intervention by integrating both observational and past interventional data collected from the system. We give theoretical results detailing how one can transfer interventional information across time steps and define a dynamic causal GP model which can be used to quantify uncertainty and find optimal interventions in practice. We demonstrate how DCBO identifies optimal interventions faster than competing approaches in multiple settings and applications.

A variational Bayesian spatial interaction model for estimating revenue and demand at business facilities

We study the problem of estimating potential revenue or demand at business facilities and understanding its generating mechanism. This problem arises in different fields such as operation research or urban science, and more generally, it is crucial for businesses' planning and decision making. We develop a Bayesian spatial interaction model, henceforth BSIM, which provides probabilistic predictions about revenues generated by a particular business location provided their features and the potential customers' characteristics in a given region. BSIM explicitly accounts for the competition among the competitive facilities through a probability value determined by evaluating a store-specific Gaussian distribution at a given customer location. We propose a scalable variational inference framework that, while being significantly faster than competing Markov Chain Monte Carlo inference schemes, exhibits comparable performances in terms of parameters identification and uncertainty quantification. We demonstrate the benefits of BSIM in various synthetic settings characterised by an increasing number of stores and customers. Finally, we construct a real-world, large spatial dataset for pub activities in London, UK, which includes over 1,500 pubs and 150,000 customer regions. We demonstrate how BSIM outperforms competing approaches on this large dataset in terms of prediction performances while providing results that are both interpretable and consistent with related indicators observed for the London region.