Automated Detection of Sport Highlights from Audio and Video Sources

This study presents a novel Deep Learning-based and lightweight approach for the automated detection of sports highlights (HLs) from audio and video sources. HL detection is a key task in sports video analysis, traditionally requiring significant human effort. Our solution leverages Deep Learning (DL) models trained on relatively small datasets of audio Mel-spectrograms and grayscale video frames, achieving promising accuracy rates of 89% and 83% for audio and video detection, respectively. The use of small datasets, combined with simple architectures, demonstrates the practicality of our method for fast and cost-effective deployment. Furthermore, an ensemble model combining both modalities shows improved robustness against false positives and false negatives. The proposed methodology offers a scalable solution for automated HL detection across various types of sports video content, reducing the need for manual intervention. Future work will focus on enhancing model architectures and extending this approach to broader scene-detection tasks in media analysis.

Edge-Wise Graph-Instructed Neural Networks

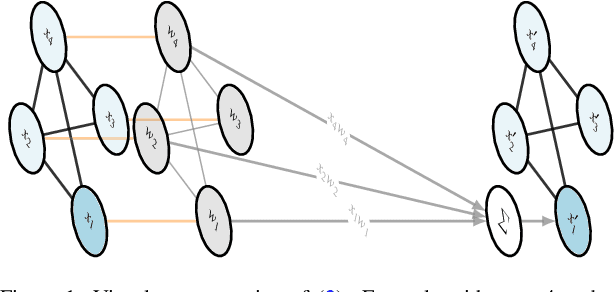
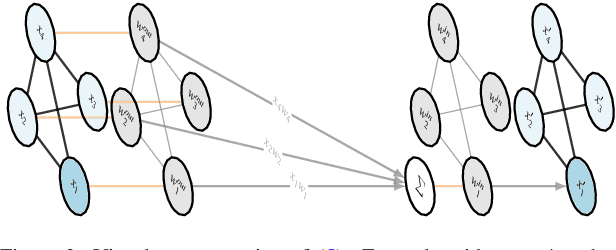
The problem of multi-task regression over graph nodes has been recently approached through Graph-Instructed Neural Network (GINN), which is a promising architecture belonging to the subset of message-passing graph neural networks. In this work, we discuss the limitations of the Graph-Instructed (GI) layer, and we formalize a novel edge-wise GI (EWGI) layer. We discuss the advantages of the EWGI layer and we provide numerical evidence that EWGINNs perform better than GINNs over graph-structured input data with chaotic connectivity, like the ones inferred from the Erdos-R\'enyi graph.

GradINN: Gradient Informed Neural Network

We propose Gradient Informed Neural Networks (GradINNs), a methodology inspired by Physics Informed Neural Networks (PINNs) that can be used to efficiently approximate a wide range of physical systems for which the underlying governing equations are completely unknown or cannot be defined, a condition that is often met in complex engineering problems. GradINNs leverage prior beliefs about a system's gradient to constrain the predicted function's gradient across all input dimensions. This is achieved using two neural networks: one modeling the target function and an auxiliary network expressing prior beliefs, e.g., smoothness. A customized loss function enables training the first network while enforcing gradient constraints derived from the auxiliary network. We demonstrate the advantages of GradINNs, particularly in low-data regimes, on diverse problems spanning non time-dependent systems (Friedman function, Stokes Flow) and time-dependent systems (Lotka-Volterra, Burger's equation). Experimental results showcase strong performance compared to standard neural networks and PINN-like approaches across all tested scenarios.

Sparse Implementation of Versatile Graph-Informed Layers

Graph Neural Networks (GNNs) have emerged as effective tools for learning tasks on graph-structured data. Recently, Graph-Informed (GI) layers were introduced to address regression tasks on graph nodes, extending their applicability beyond classic GNNs. However, existing implementations of GI layers lack efficiency due to dense memory allocation. This paper presents a sparse implementation of GI layers, leveraging the sparsity of adjacency matrices to reduce memory usage significantly. Additionally, a versatile general form of GI layers is introduced, enabling their application to subsets of graph nodes. The proposed sparse implementation improves the concrete computational efficiency and scalability of the GI layers, permitting to build deeper Graph-Informed Neural Networks (GINNs) and facilitating their scalability to larger graphs.

Graph-Informed Neural Networks for Sparse Grid-Based Discontinuity Detectors

In this paper, we present a novel approach for detecting the discontinuity interfaces of a discontinuous function. This approach leverages Graph-Informed Neural Networks (GINNs) and sparse grids to address discontinuity detection also in domains of dimension larger than 3. GINNs, trained to identify troubled points on sparse grids, exploit graph structures built on the grids to achieve efficient and accurate discontinuity detection performances. We also introduce a recursive algorithm for general sparse grid-based detectors, characterized by convergence properties and easy applicability. Numerical experiments on functions with dimensions n = 2 and n = 4 demonstrate the efficiency and robust generalization of GINNs in detecting discontinuity interfaces. Notably, the trained GINNs offer portability and versatility, allowing integration into various algorithms and sharing among users.

Alternate Training of Shared and Task-Specific Parameters for Multi-Task Neural Networks

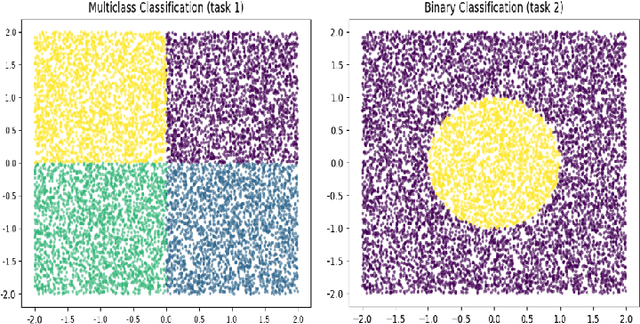
This paper introduces novel alternate training procedures for hard-parameter sharing Multi-Task Neural Networks (MTNNs). Traditional MTNN training faces challenges in managing conflicting loss gradients, often yielding sub-optimal performance. The proposed alternate training method updates shared and task-specific weights alternately, exploiting the multi-head architecture of the model. This approach reduces computational costs, enhances training regularization, and improves generalization. Convergence properties similar to those of the classical stochastic gradient method are established. Empirical experiments demonstrate delayed overfitting, improved prediction, and reduced computational demands. In summary, our alternate training procedures offer a promising advancement for the training of hard-parameter sharing MTNNs.