Attributes Shape the Embedding Space of Face Recognition Models

Face Recognition (FR) tasks have made significant progress with the advent of Deep Neural Networks, particularly through margin-based triplet losses that embed facial images into high-dimensional feature spaces. During training, these contrastive losses focus exclusively on identity information as labels. However, we observe a multiscale geometric structure emerging in the embedding space, influenced by interpretable facial (e.g., hair color) and image attributes (e.g., contrast). We propose a geometric approach to describe the dependence or invariance of FR models to these attributes and introduce a physics-inspired alignment metric. We evaluate the proposed metric on controlled, simplified models and widely used FR models fine-tuned with synthetic data for targeted attribute augmentation. Our findings reveal that the models exhibit varying degrees of invariance across different attributes, providing insight into their strengths and weaknesses and enabling deeper interpretability. Code available here: https://github.com/mantonios107/attrs-fr-embs}{https://github.com/mantonios107/attrs-fr-embs

Topological obstruction to the training of shallow ReLU neural networks

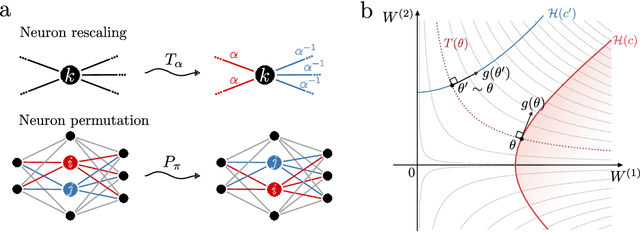
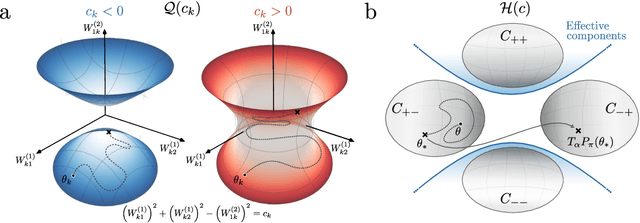
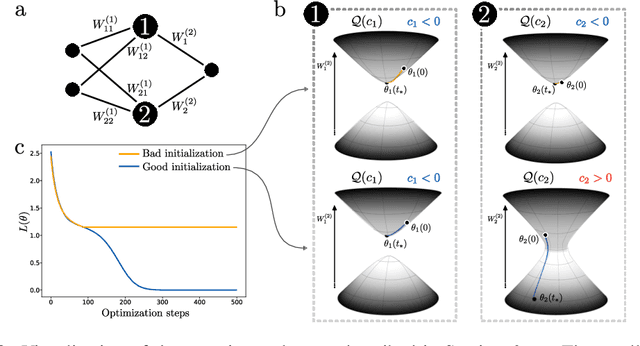
Studying the interplay between the geometry of the loss landscape and the optimization trajectories of simple neural networks is a fundamental step for understanding their behavior in more complex settings. This paper reveals the presence of topological obstruction in the loss landscape of shallow ReLU neural networks trained using gradient flow. We discuss how the homogeneous nature of the ReLU activation function constrains the training trajectories to lie on a product of quadric hypersurfaces whose shape depends on the particular initialization of the network's parameters. When the neural network's output is a single scalar, we prove that these quadrics can have multiple connected components, limiting the set of reachable parameters during training. We analytically compute the number of these components and discuss the possibility of mapping one to the other through neuron rescaling and permutation. In this simple setting, we find that the non-connectedness results in a topological obstruction, which, depending on the initialization, can make the global optimum unreachable. We validate this result with numerical experiments.

Edge-Wise Graph-Instructed Neural Networks

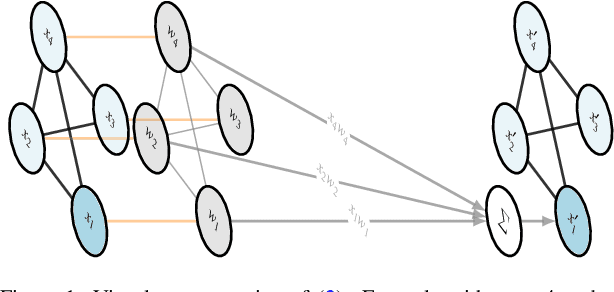
The problem of multi-task regression over graph nodes has been recently approached through Graph-Instructed Neural Network (GINN), which is a promising architecture belonging to the subset of message-passing graph neural networks. In this work, we discuss the limitations of the Graph-Instructed (GI) layer, and we formalize a novel edge-wise GI (EWGI) layer. We discuss the advantages of the EWGI layer and we provide numerical evidence that EWGINNs perform better than GINNs over graph-structured input data with chaotic connectivity, like the ones inferred from the Erdos-R\'enyi graph.

ICML Topological Deep Learning Challenge 2024: Beyond the Graph Domain

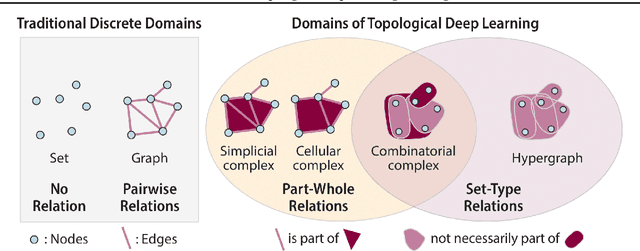
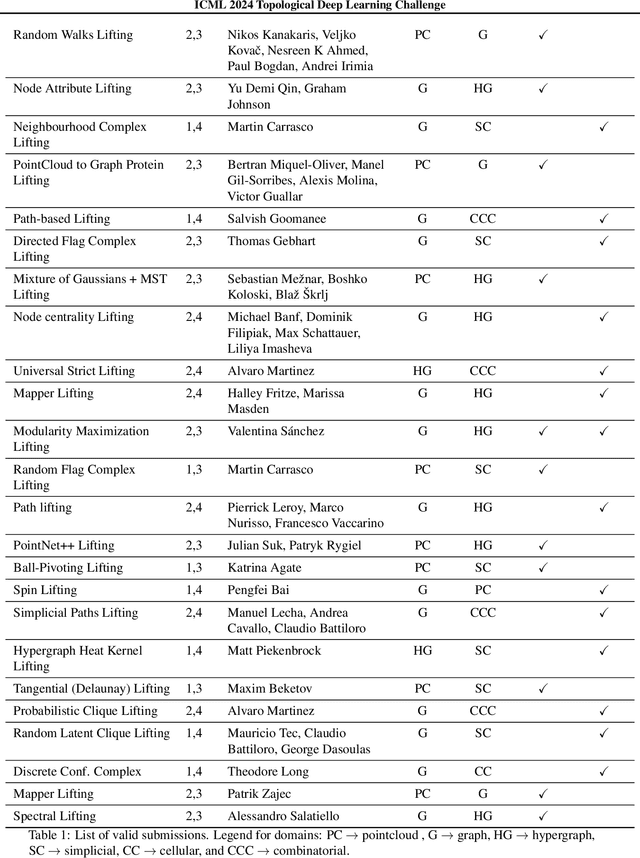
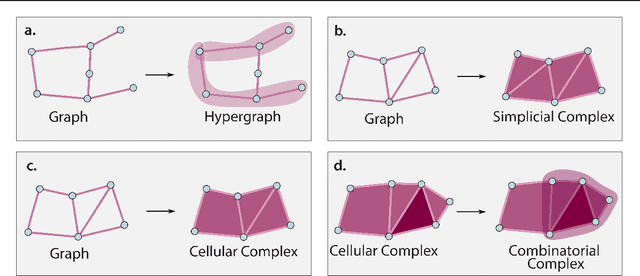
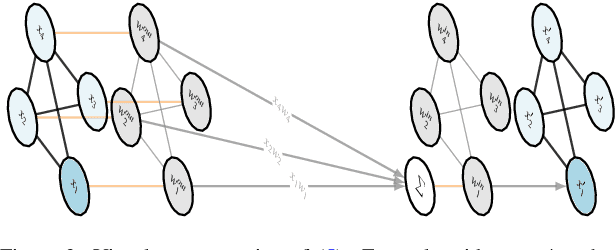
This paper describes the 2nd edition of the ICML Topological Deep Learning Challenge that was hosted within the ICML 2024 ELLIS Workshop on Geometry-grounded Representation Learning and Generative Modeling (GRaM). The challenge focused on the problem of representing data in different discrete topological domains in order to bridge the gap between Topological Deep Learning (TDL) and other types of structured datasets (e.g. point clouds, graphs). Specifically, participants were asked to design and implement topological liftings, i.e. mappings between different data structures and topological domains --like hypergraphs, or simplicial/cell/combinatorial complexes. The challenge received 52 submissions satisfying all the requirements. This paper introduces the main scope of the challenge, and summarizes the main results and findings.

Scale-Free Image Keypoints Using Differentiable Persistent Homology

In computer vision, keypoint detection is a fundamental task, with applications spanning from robotics to image retrieval; however, existing learning-based methods suffer from scale dependency and lack flexibility. This paper introduces a novel approach that leverages Morse theory and persistent homology, powerful tools rooted in algebraic topology. We propose a novel loss function based on the recent introduction of a notion of subgradient in persistent homology, paving the way toward topological learning. Our detector, MorseDet, is the first topology-based learning model for feature detection, which achieves competitive performance in keypoint repeatability and introduces a principled and theoretically robust approach to the problem.