Topological Deep Learning with State-Space Models: A Mamba Approach for Simplicial Complexes

Graph Neural Networks based on the message-passing (MP) mechanism are a dominant approach for handling graph-structured data. However, they are inherently limited to modeling only pairwise interactions, making it difficult to explicitly capture the complexity of systems with $n$-body relations. To address this, topological deep learning has emerged as a promising field for studying and modeling higher-order interactions using various topological domains, such as simplicial and cellular complexes. While these new domains provide powerful representations, they introduce new challenges, such as effectively modeling the interactions among higher-order structures through higher-order MP. Meanwhile, structured state-space sequence models have proven to be effective for sequence modeling and have recently been adapted for graph data by encoding the neighborhood of a node as a sequence, thereby avoiding the MP mechanism. In this work, we propose a novel architecture designed to operate with simplicial complexes, utilizing the Mamba state-space model as its backbone. Our approach generates sequences for the nodes based on the neighboring cells, enabling direct communication between all higher-order structures, regardless of their rank. We extensively validate our model, demonstrating that it achieves competitive performance compared to state-of-the-art models developed for simplicial complexes.

ICML Topological Deep Learning Challenge 2024: Beyond the Graph Domain

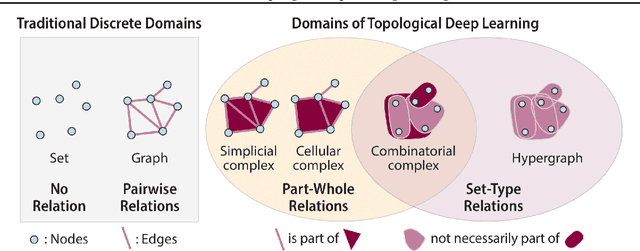
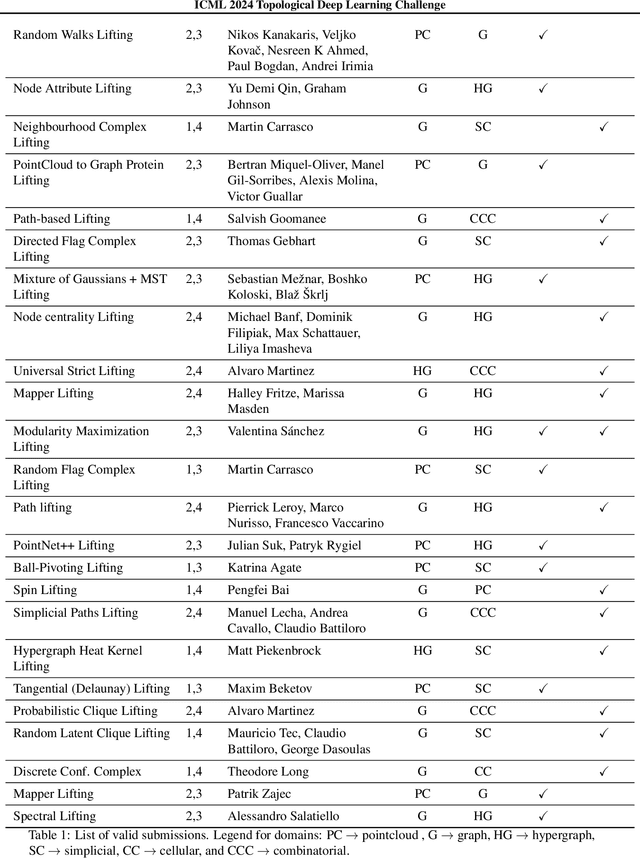
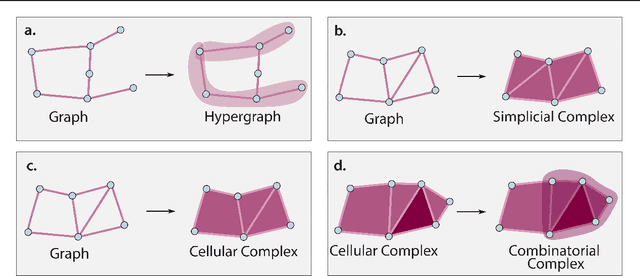
This paper describes the 2nd edition of the ICML Topological Deep Learning Challenge that was hosted within the ICML 2024 ELLIS Workshop on Geometry-grounded Representation Learning and Generative Modeling (GRaM). The challenge focused on the problem of representing data in different discrete topological domains in order to bridge the gap between Topological Deep Learning (TDL) and other types of structured datasets (e.g. point clouds, graphs). Specifically, participants were asked to design and implement topological liftings, i.e. mappings between different data structures and topological domains --like hypergraphs, or simplicial/cell/combinatorial complexes. The challenge received 52 submissions satisfying all the requirements. This paper introduces the main scope of the challenge, and summarizes the main results and findings.

TopoBenchmarkX: A Framework for Benchmarking Topological Deep Learning

This work introduces TopoBenchmarkX, a modular open-source library designed to standardize benchmarking and accelerate research in Topological Deep Learning (TDL). TopoBenchmarkX maps the TDL pipeline into a sequence of independent and modular components for data loading and processing, as well as model training, optimization, and evaluation. This modular organization provides flexibility for modifications and facilitates the adaptation and optimization of various TDL pipelines. A key feature of TopoBenchmarkX is that it allows for the transformation and lifting between topological domains. This enables, for example, to obtain richer data representations and more fine-grained analyses by mapping the topology and features of a graph to higher-order topological domains such as simplicial and cell complexes. The range of applicability of TopoBenchmarkX is demonstrated by benchmarking several TDL architectures for various tasks and datasets.

TopoX: A Suite of Python Packages for Machine Learning on Topological Domains

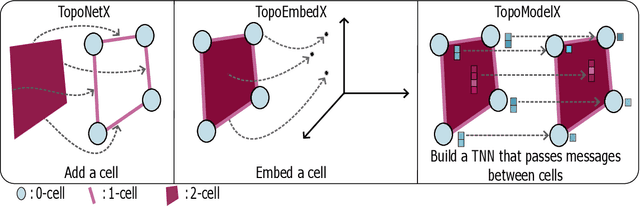
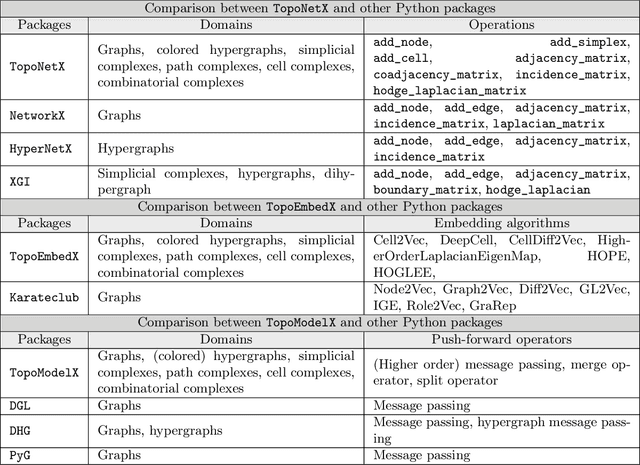
We introduce topox, a Python software suite that provides reliable and user-friendly building blocks for computing and machine learning on topological domains that extend graphs: hypergraphs, simplicial, cellular, path and combinatorial complexes. topox consists of three packages: toponetx facilitates constructing and computing on these domains, including working with nodes, edges and higher-order cells; topoembedx provides methods to embed topological domains into vector spaces, akin to popular graph-based embedding algorithms such as node2vec; topomodelx is built on top of PyTorch and offers a comprehensive toolbox of higher-order message passing functions for neural networks on topological domains. The extensively documented and unit-tested source code of topox is available under MIT license at https://github.com/pyt-team.

Hypergraph Neural Networks through the Lens of Message Passing: A Common Perspective to Homophily and Architecture Design

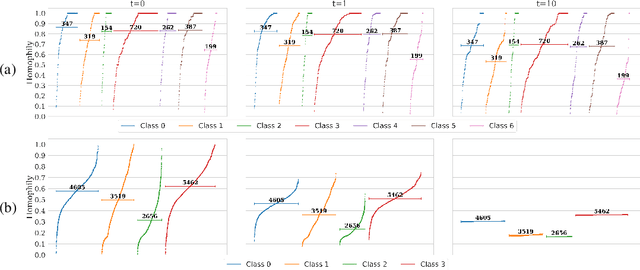
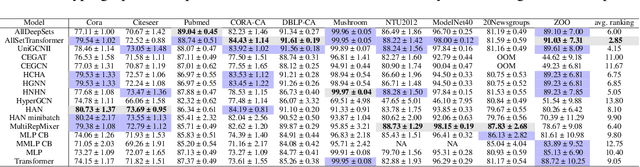
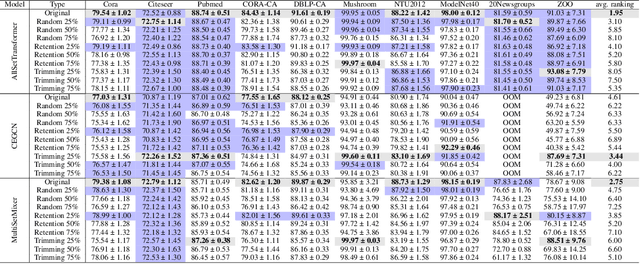
Most of the current hypergraph learning methodologies and benchmarking datasets in the hypergraph realm are obtained by lifting procedures from their graph analogs, simultaneously leading to overshadowing hypergraph network foundations. This paper attempts to confront some pending questions in that regard: Can the concept of homophily play a crucial role in Hypergraph Neural Networks (HGNNs), similar to its significance in graph-based research? Is there room for improving current hypergraph architectures and methodologies? (e.g. by carefully addressing the specific characteristics of higher-order networks) Do existing datasets provide a meaningful benchmark for HGNNs? Diving into the details, this paper proposes a novel conceptualization of homophily in higher-order networks based on a message passing scheme; this approach harmonizes the analytical frameworks of datasets and architectures, offering a unified perspective for exploring and interpreting complex, higher-order network structures and dynamics. Further, we propose MultiSet, a novel message passing framework that redefines HGNNs by allowing hyperedge-dependent node representations, as well as introduce a novel architecture MultiSetMixer that leverages a new hyperedge sampling strategy. Finally, we provide an extensive set of experiments that contextualize our proposals and lead to valuable insights in hypergraph representation learning.

ICML 2023 Topological Deep Learning Challenge : Design and Results

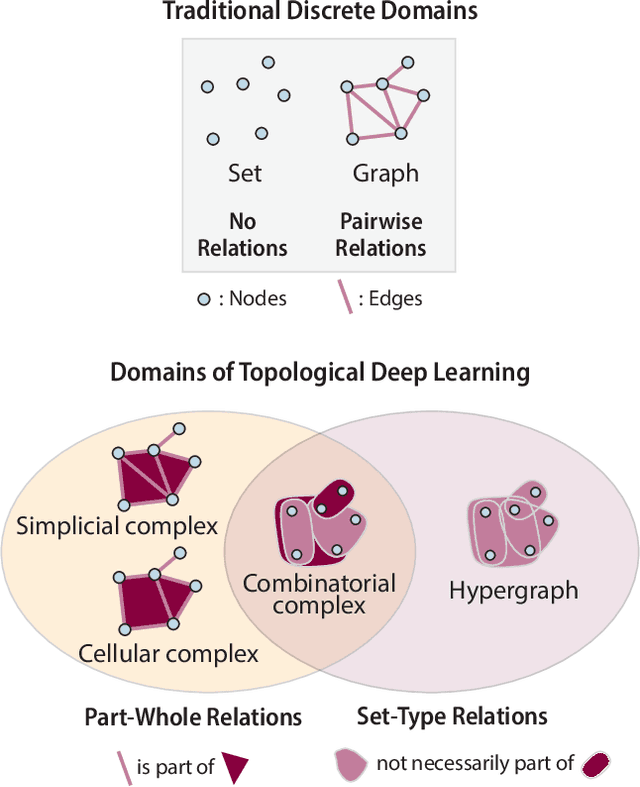
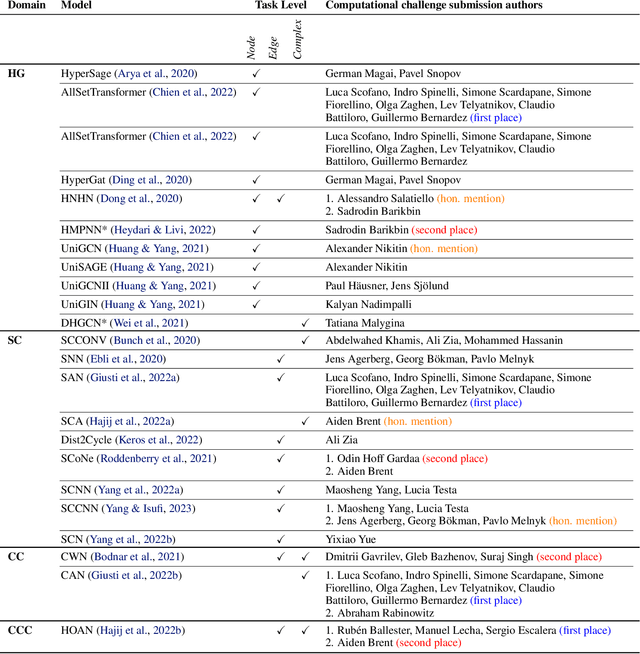
This paper presents the computational challenge on topological deep learning that was hosted within the ICML 2023 Workshop on Topology and Geometry in Machine Learning. The competition asked participants to provide open-source implementations of topological neural networks from the literature by contributing to the python packages TopoNetX (data processing) and TopoModelX (deep learning). The challenge attracted twenty-eight qualifying submissions in its two-month duration. This paper describes the design of the challenge and summarizes its main findings.

Topological Graph Signal Compression

Recently emerged Topological Deep Learning (TDL) methods aim to extend current Graph Neural Networks (GNN) by naturally processing higher-order interactions, going beyond the pairwise relations and local neighborhoods defined by graph representations. In this paper we propose a novel TDL-based method for compressing signals over graphs, consisting in two main steps: first, disjoint sets of higher-order structures are inferred based on the original signal --by clustering $N$ datapoints into $K\ll N$ collections; then, a topological-inspired message passing gets a compressed representation of the signal within those multi-element sets. Our results show that our framework improves both standard GNN and feed-forward architectures in compressing temporal link-based signals from two real-word Internet Service Provider Networks' datasets --from $30\%$ up to $90\%$ better reconstruction errors across all evaluation scenarios--, suggesting that it better captures and exploits spatial and temporal correlations over the whole graph-based network structure.

From Latent Graph to Latent Topology Inference: Differentiable Cell Complex Module

Latent Graph Inference (LGI) relaxed the reliance of Graph Neural Networks (GNNs) on a given graph topology by dynamically learning it. However, most of LGI methods assume to have a (noisy, incomplete, improvable, ...) input graph to rewire and can solely learn regular graph topologies. In the wake of the success of Topological Deep Learning (TDL), we study Latent Topology Inference (LTI) for learning higher-order cell complexes (with sparse and not regular topology) describing multi-way interactions between data points. To this aim, we introduce the Differentiable Cell Complex Module (DCM), a novel learnable function that computes cell probabilities in the complex to improve the downstream task. We show how to integrate DCM with cell complex message passing networks layers and train it in a end-to-end fashion, thanks to a two-step inference procedure that avoids an exhaustive search across all possible cells in the input, thus maintaining scalability. Our model is tested on several homophilic and heterophilic graph datasets and it is shown to outperform other state-of-the-art techniques, offering significant improvements especially in cases where an input graph is not provided.

EGG-GAE: scalable graph neural networks for tabular data imputation

Missing data imputation (MDI) is crucial when dealing with tabular datasets across various domains. Autoencoders can be trained to reconstruct missing values, and graph autoencoders (GAE) can additionally consider similar patterns in the dataset when imputing new values for a given instance. However, previously proposed GAEs suffer from scalability issues, requiring the user to define a similarity metric among patterns to build the graph connectivity beforehand. In this paper, we leverage recent progress in latent graph imputation to propose a novel EdGe Generation Graph AutoEncoder (EGG-GAE) for missing data imputation that overcomes these two drawbacks. EGG-GAE works on randomly sampled mini-batches of the input data (hence scaling to larger datasets), and it automatically infers the best connectivity across the mini-batch for each architecture layer. We also experiment with several extensions, including an ensemble strategy for inference and the inclusion of what we call prototype nodes, obtaining significant improvements, both in terms of imputation error and final downstream accuracy, across multiple benchmarks and baselines.