MASS: MoErging through Adaptive Subspace Selection

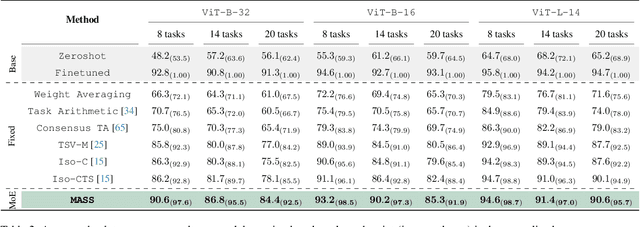
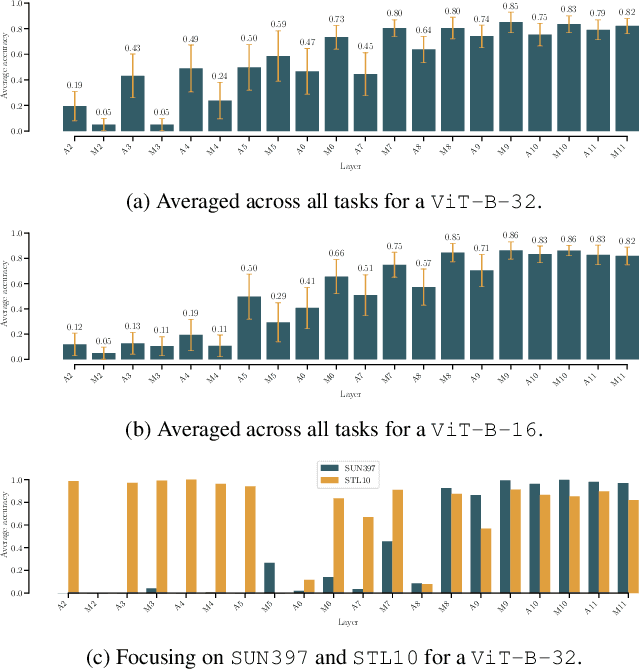
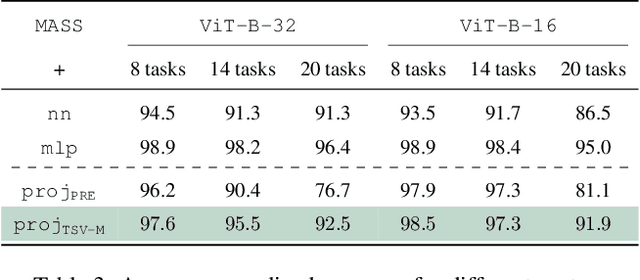
Model merging has recently emerged as a lightweight alternative to ensembling, combining multiple fine-tuned models into a single set of parameters with no additional training overhead. Yet, existing merging methods fall short of matching the full accuracy of separately fine-tuned endpoints. We present MASS (MoErging through Adaptive Subspace Selection), a new approach that closes this gap by unifying multiple fine-tuned models while retaining near state-of-the-art performance across tasks. Building on the low-rank decomposition of per-task updates, MASS stores only the most salient singular components for each task and merges them into a shared model. At inference time, a non-parametric, data-free router identifies which subspace (or combination thereof) best explains an input's intermediate features and activates the corresponding task-specific block. This procedure is fully training-free and introduces only a two-pass inference overhead plus a ~2 storage factor compared to a single pretrained model, irrespective of the number of tasks. We evaluate MASS on CLIP-based image classification using ViT-B-16, ViT-B-32 and ViT-L-14 for benchmarks of 8, 14 and 20 tasks respectively, establishing a new state-of-the-art. Most notably, MASS recovers up to ~98% of the average accuracy of individual fine-tuned models, making it a practical alternative to ensembling at a fraction of the storage cost.

The Majority Vote Paradigm Shift: When Popular Meets Optimal

Reliably labelling data typically requires annotations from multiple human workers. However, humans are far from being perfect. Hence, it is a common practice to aggregate labels gathered from multiple annotators to make a more confident estimate of the true label. Among many aggregation methods, the simple and well known Majority Vote (MV) selects the class label polling the highest number of votes. However, despite its importance, the optimality of MV's label aggregation has not been extensively studied. We address this gap in our work by characterising the conditions under which MV achieves the theoretically optimal lower bound on label estimation error. Our results capture the tolerable limits on annotation noise under which MV can optimally recover labels for a given class distribution. This certificate of optimality provides a more principled approach to model selection for label aggregation as an alternative to otherwise inefficient practices that sometimes include higher experts, gold labels, etc., that are all marred by the same human uncertainty despite huge time and monetary costs. Experiments on both synthetic and real world data corroborate our theoretical findings.

Robustness of Graph Classification: failure modes, causes, and noise-resistant loss in Graph Neural Networks

Graph Neural Networks (GNNs) are powerful at solving graph classification tasks, yet applied problems often contain noisy labels. In this work, we study GNN robustness to label noise, demonstrate GNN failure modes when models struggle to generalise on low-order graphs, low label coverage, or when a model is over-parameterized. We establish both empirical and theoretical links between GNN robustness and the reduction of the total Dirichlet Energy of learned node representations, which encapsulates the hypothesized GNN smoothness inductive bias. Finally, we introduce two training strategies to enhance GNN robustness: (1) by incorporating a novel inductive bias in the weight matrices through the removal of negative eigenvalues, connected to Dirichlet Energy minimization; (2) by extending to GNNs a loss penalty that promotes learned smoothness. Importantly, neither approach negatively impacts performance in noise-free settings, supporting our hypothesis that the source of GNNs robustness is their smoothness inductive bias.

Task Singular Vectors: Reducing Task Interference in Model Merging

Task Arithmetic has emerged as a simple yet effective method to merge models without additional training. However, by treating entire networks as flat parameter vectors, it overlooks key structural information and is susceptible to task interference. In this paper, we study task vectors at the layer level, focusing on task layer matrices and their singular value decomposition. In particular, we concentrate on the resulting singular vectors, which we refer to as Task Singular Vectors (TSV). Recognizing that layer task matrices are often low-rank, we propose TSV-Compress (TSV-C), a simple procedure that compresses them to 10% of their original size while retaining 99% of accuracy. We further leverage this low-rank space to define a new measure of task interference based on the interaction of singular vectors from different tasks. Building on these findings, we introduce TSV-Merge (TSV-M), a novel model merging approach that combines compression with interference reduction, significantly outperforming existing methods.

ATM: Improving Model Merging by Alternating Tuning and Merging

Model merging has recently emerged as a cost-efficient paradigm for multi-task learning. Among current approaches, task arithmetic stands out for its simplicity and effectiveness. In this paper, we motivate the effectiveness of task vectors by linking them to multi-task gradients. We show that in a single-epoch scenario, task vectors are mathematically equivalent to the gradients obtained via gradient descent in a multi-task setting, and still approximate these gradients in subsequent epochs. Furthermore, we show that task vectors perform optimally when equality is maintained, and their effectiveness is largely driven by the first epoch's gradient. Building on this insight, we propose viewing model merging as a single step in an iterative process that Alternates between Tuning and Merging (ATM). This method acts as a bridge between model merging and multi-task gradient descent, achieving state-of-the-art results with the same data and computational requirements. We extensively evaluate ATM across diverse settings, achieving up to 20% higher accuracy in computer vision and NLP tasks, compared to the best baselines.Finally, we provide both empirical and theoretical support for its effectiveness, demonstrating increased orthogonality between task vectors and proving that ATM minimizes an upper bound on the loss obtained by jointly finetuning all tasks.

ICML Topological Deep Learning Challenge 2024: Beyond the Graph Domain

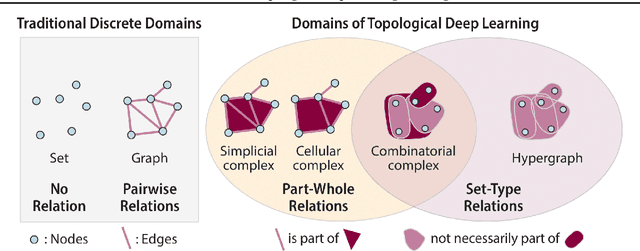
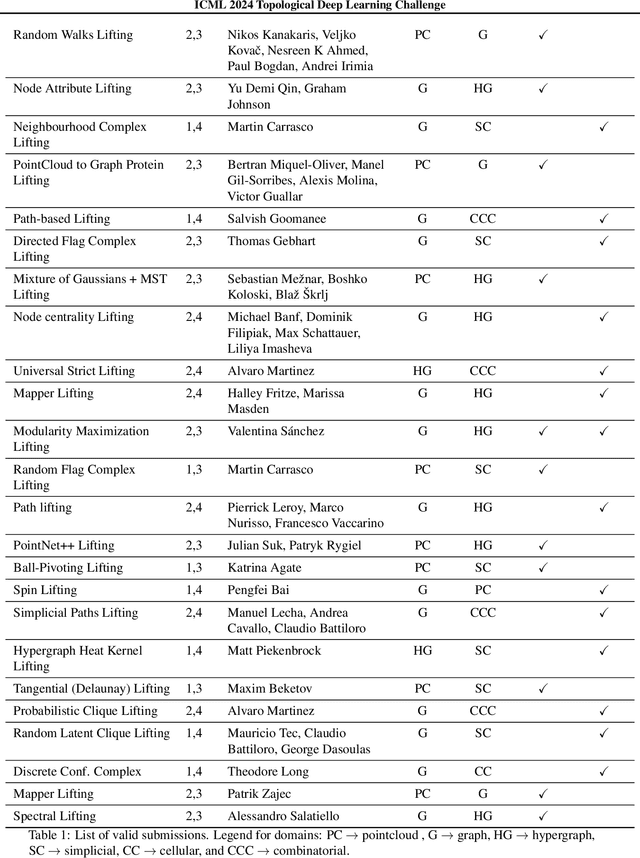
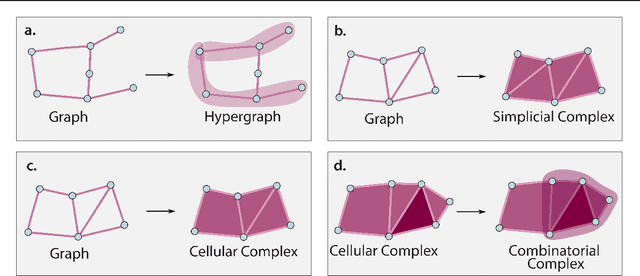
This paper describes the 2nd edition of the ICML Topological Deep Learning Challenge that was hosted within the ICML 2024 ELLIS Workshop on Geometry-grounded Representation Learning and Generative Modeling (GRaM). The challenge focused on the problem of representing data in different discrete topological domains in order to bridge the gap between Topological Deep Learning (TDL) and other types of structured datasets (e.g. point clouds, graphs). Specifically, participants were asked to design and implement topological liftings, i.e. mappings between different data structures and topological domains --like hypergraphs, or simplicial/cell/combinatorial complexes. The challenge received 52 submissions satisfying all the requirements. This paper introduces the main scope of the challenge, and summarizes the main results and findings.

$ abla τ$: Gradient-based and Task-Agnostic machine Unlearning

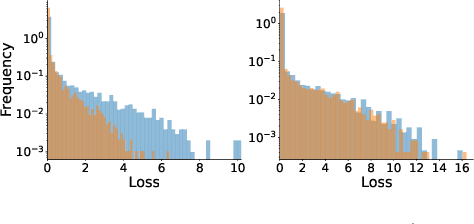
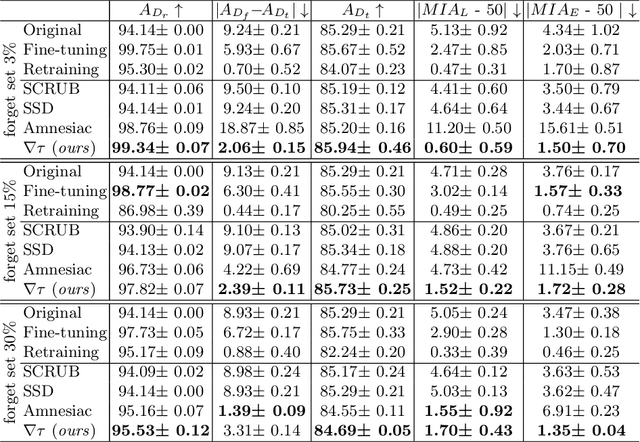
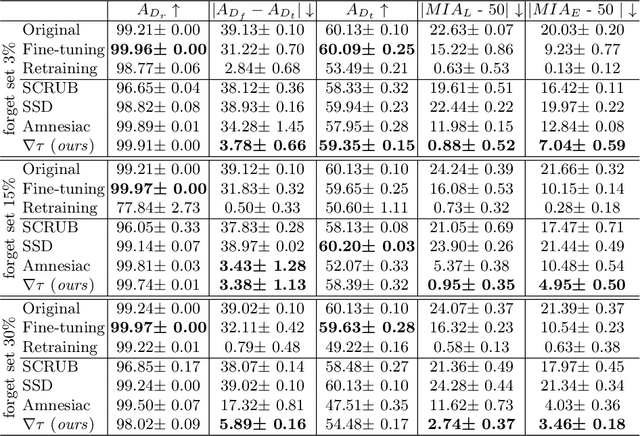
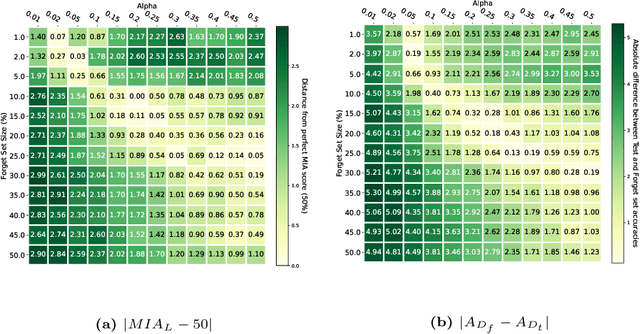
Machine Unlearning, the process of selectively eliminating the influence of certain data examples used during a model's training, has gained significant attention as a means for practitioners to comply with recent data protection regulations. However, existing unlearning methods face critical drawbacks, including their prohibitively high cost, often associated with a large number of hyperparameters, and the limitation of forgetting only relatively small data portions. This often makes retraining the model from scratch a quicker and more effective solution. In this study, we introduce Gradient-based and Task-Agnostic machine Unlearning ($\nabla \tau$), an optimization framework designed to remove the influence of a subset of training data efficiently. It applies adaptive gradient ascent to the data to be forgotten while using standard gradient descent for the remaining data. $\nabla \tau$ offers multiple benefits over existing approaches. It enables the unlearning of large sections of the training dataset (up to 30%). It is versatile, supporting various unlearning tasks (such as subset forgetting or class removal) and applicable across different domains (images, text, etc.). Importantly, $\nabla \tau$ requires no hyperparameter adjustments, making it a more appealing option than retraining the model from scratch. We evaluate our framework's effectiveness using a set of well-established Membership Inference Attack metrics, demonstrating up to 10% enhancements in performance compared to state-of-the-art methods without compromising the original model's accuracy.

Link Prediction under Heterophily: A Physics-Inspired Graph Neural Network Approach

In the past years, Graph Neural Networks (GNNs) have become the `de facto' standard in various deep learning domains, thanks to their flexibility in modeling real-world phenomena represented as graphs. However, the message-passing mechanism of GNNs faces challenges in learnability and expressivity, hindering high performance on heterophilic graphs, where adjacent nodes frequently have different labels. Most existing solutions addressing these challenges are primarily confined to specific benchmarks focused on node classification tasks. This narrow focus restricts the potential impact that link prediction under heterophily could offer in several applications, including recommender systems. For example, in social networks, two users may be connected for some latent reason, making it challenging to predict such connections in advance. Physics-Inspired GNNs such as GRAFF provided a significant contribution to enhance node classification performance under heterophily, thanks to the adoption of physics biases in the message-passing. Drawing inspiration from these findings, we advocate that the methodology employed by GRAFF can improve link prediction performance as well. To further explore this hypothesis, we introduce GRAFF-LP, an extension of GRAFF to link prediction. We evaluate its efficacy within a recent collection of heterophilic graphs, establishing a new benchmark for link prediction under heterophily. Our approach surpasses previous methods, in most of the datasets, showcasing a strong flexibility in different contexts, and achieving relative AUROC improvements of up to 26.7%.

A topological description of loss surfaces based on Betti Numbers

In the context of deep learning models, attention has recently been paid to studying the surface of the loss function in order to better understand training with methods based on gradient descent. This search for an appropriate description, both analytical and topological, has led to numerous efforts to identify spurious minima and characterize gradient dynamics. Our work aims to contribute to this field by providing a topological measure to evaluate loss complexity in the case of multilayer neural networks. We compare deep and shallow architectures with common sigmoidal activation functions by deriving upper and lower bounds on the complexity of their loss function and revealing how that complexity is influenced by the number of hidden units, training models, and the activation function used. Additionally, we found that certain variations in the loss function or model architecture, such as adding an $\ell_2$ regularization term or implementing skip connections in a feedforward network, do not affect loss topology in specific cases.

On Generalization Bounds for Projective Clustering

Given a set of points, clustering consists of finding a partition of a point set into $k$ clusters such that the center to which a point is assigned is as close as possible. Most commonly, centers are points themselves, which leads to the famous $k$-median and $k$-means objectives. One may also choose centers to be $j$ dimensional subspaces, which gives rise to subspace clustering. In this paper, we consider learning bounds for these problems. That is, given a set of $n$ samples $P$ drawn independently from some unknown, but fixed distribution $\mathcal{D}$, how quickly does a solution computed on $P$ converge to the optimal clustering of $\mathcal{D}$? We give several near optimal results. In particular, For center-based objectives, we show a convergence rate of $\tilde{O}\left(\sqrt{{k}/{n}}\right)$. This matches the known optimal bounds of [Fefferman, Mitter, and Narayanan, Journal of the Mathematical Society 2016] and [Bartlett, Linder, and Lugosi, IEEE Trans. Inf. Theory 1998] for $k$-means and extends it to other important objectives such as $k$-median. For subspace clustering with $j$-dimensional subspaces, we show a convergence rate of $\tilde{O}\left(\sqrt{\frac{kj^2}{n}}\right)$. These are the first provable bounds for most of these problems. For the specific case of projective clustering, which generalizes $k$-means, we show a convergence rate of $\Omega\left(\sqrt{\frac{kj}{n}}\right)$ is necessary, thereby proving that the bounds from [Fefferman, Mitter, and Narayanan, Journal of the Mathematical Society 2016] are essentially optimal.