Implicit Inversion turns CLIP into a Decoder

CLIP is a discriminative model trained to align images and text in a shared embedding space. Due to its multimodal structure, it serves as the backbone of many generative pipelines, where a decoder is trained to map from the shared space back to images. In this work, we show that image synthesis is nevertheless possible using CLIP alone -- without any decoder, training, or fine-tuning. Our approach optimizes a frequency-aware implicit neural representation that encourages coarse-to-fine generation by stratifying frequencies across network layers. To stabilize this inverse mapping, we introduce adversarially robust initialization, a lightweight Orthogonal Procrustes projection to align local text and image embeddings, and a blending loss that anchors outputs to natural image statistics. Without altering CLIP's weights, this framework unlocks capabilities such as text-to-image generation, style transfer, and image reconstruction. These findings suggest that discriminative models may hold untapped generative potential, hidden in plain sight.

Update Your Transformer to the Latest Release: Re-Basin of Task Vectors

Foundation models serve as the backbone for numerous specialized models developed through fine-tuning. However, when the underlying pretrained model is updated or retrained (e.g., on larger and more curated datasets), the fine-tuned model becomes obsolete, losing its utility and requiring retraining. This raises the question: is it possible to transfer fine-tuning to a new release of the model? In this work, we investigate how to transfer fine-tuning to a new checkpoint without having to re-train, in a data-free manner. To do so, we draw principles from model re-basin and provide a recipe based on weight permutations to re-base the modifications made to the original base model, often called task vector. In particular, our approach tailors model re-basin for Transformer models, taking into account the challenges of residual connections and multi-head attention layers. Specifically, we propose a two-level method rooted in spectral theory, initially permuting the attention heads and subsequently adjusting parameters within select pairs of heads. Through extensive experiments on visual and textual tasks, we achieve the seamless transfer of fine-tuned knowledge to new pre-trained backbones without relying on a single training step or datapoint. Code is available at https://github.com/aimagelab/TransFusion.

Mergenetic: a Simple Evolutionary Model Merging Library

Model merging allows combining the capabilities of existing models into a new one - post hoc, without additional training. This has made it increasingly popular thanks to its low cost and the availability of libraries that support merging on consumer GPUs. Recent work shows that pairing merging with evolutionary algorithms can boost performance, but no framework currently supports flexible experimentation with such strategies in language models. We introduce Mergenetic, an open-source library for evolutionary model merging. Mergenetic enables easy composition of merging methods and evolutionary algorithms while incorporating lightweight fitness estimators to reduce evaluation costs. We describe its design and demonstrate that Mergenetic produces competitive results across tasks and languages using modest hardware.

STAGE: Stemmed Accompaniment Generation through Prefix-Based Conditioning

Recent advances in generative models have made it possible to create high-quality, coherent music, with some systems delivering production-level output. Yet, most existing models focus solely on generating music from scratch, limiting their usefulness for musicians who want to integrate such models into a human, iterative composition workflow. In this paper we introduce STAGE, our STemmed Accompaniment GEneration model, fine-tuned from the state-of-the-art MusicGen to generate single-stem instrumental accompaniments conditioned on a given mixture. Inspired by instruction-tuning methods for language models, we extend the transformer's embedding matrix with a context token, enabling the model to attend to a musical context through prefix-based conditioning. Compared to the baselines, STAGE yields accompaniments that exhibit stronger coherence with the input mixture, higher audio quality, and closer alignment with textual prompts. Moreover, by conditioning on a metronome-like track, our framework naturally supports tempo-constrained generation, achieving state-of-the-art alignment with the target rhythmic structure--all without requiring any additional tempo-specific module. As a result, STAGE offers a practical, versatile tool for interactive music creation that can be readily adopted by musicians in real-world workflows.

LoopGen: Training-Free Loopable Music Generation

Loops--short audio segments designed for seamless repetition--are central to many music genres, particularly those rooted in dance and electronic styles. However, current generative music models struggle to produce truly loopable audio, as generating a short waveform alone does not guarantee a smooth transition from its endpoint back to its start, often resulting in audible discontinuities. Loops--short audio segments designed for seamless repetition--are central to many music genres, particularly those rooted in dance and electronic styles. However, current generative music models struggle to produce truly loopable audio, as generating a short waveform alone does not guarantee a smooth transition from its endpoint back to its start, often resulting in audible discontinuities. We address this gap by modifying a non-autoregressive model (MAGNeT) to generate tokens in a circular pattern, letting the model attend to the beginning of the audio when creating its ending. This inference-only approach results in generations that are aware of future context and loop naturally, without the need for any additional training or data. We evaluate the consistency of loop transitions by computing token perplexity around the seam of the loop, observing a 55% improvement. Blind listening tests further confirm significant perceptual gains over baseline methods, improving mean ratings by 70%. Taken together, these results highlight the effectiveness of inference-only approaches in improving generative models and underscore the advantages of non-autoregressive methods for context-aware music generation.

MASS: MoErging through Adaptive Subspace Selection

Model merging has recently emerged as a lightweight alternative to ensembling, combining multiple fine-tuned models into a single set of parameters with no additional training overhead. Yet, existing merging methods fall short of matching the full accuracy of separately fine-tuned endpoints. We present MASS (MoErging through Adaptive Subspace Selection), a new approach that closes this gap by unifying multiple fine-tuned models while retaining near state-of-the-art performance across tasks. Building on the low-rank decomposition of per-task updates, MASS stores only the most salient singular components for each task and merges them into a shared model. At inference time, a non-parametric, data-free router identifies which subspace (or combination thereof) best explains an input's intermediate features and activates the corresponding task-specific block. This procedure is fully training-free and introduces only a two-pass inference overhead plus a ~2 storage factor compared to a single pretrained model, irrespective of the number of tasks. We evaluate MASS on CLIP-based image classification using ViT-B-16, ViT-B-32 and ViT-L-14 for benchmarks of 8, 14 and 20 tasks respectively, establishing a new state-of-the-art. Most notably, MASS recovers up to ~98% of the average accuracy of individual fine-tuned models, making it a practical alternative to ensembling at a fraction of the storage cost.

Humanity's Last Exam

Benchmarks are important tools for tracking the rapid advancements in large language model (LLM) capabilities. However, benchmarks are not keeping pace in difficulty: LLMs now achieve over 90\% accuracy on popular benchmarks like MMLU, limiting informed measurement of state-of-the-art LLM capabilities. In response, we introduce Humanity's Last Exam (HLE), a multi-modal benchmark at the frontier of human knowledge, designed to be the final closed-ended academic benchmark of its kind with broad subject coverage. HLE consists of 3,000 questions across dozens of subjects, including mathematics, humanities, and the natural sciences. HLE is developed globally by subject-matter experts and consists of multiple-choice and short-answer questions suitable for automated grading. Each question has a known solution that is unambiguous and easily verifiable, but cannot be quickly answered via internet retrieval. State-of-the-art LLMs demonstrate low accuracy and calibration on HLE, highlighting a significant gap between current LLM capabilities and the expert human frontier on closed-ended academic questions. To inform research and policymaking upon a clear understanding of model capabilities, we publicly release HLE at https://lastexam.ai.

Task Singular Vectors: Reducing Task Interference in Model Merging

Task Arithmetic has emerged as a simple yet effective method to merge models without additional training. However, by treating entire networks as flat parameter vectors, it overlooks key structural information and is susceptible to task interference. In this paper, we study task vectors at the layer level, focusing on task layer matrices and their singular value decomposition. In particular, we concentrate on the resulting singular vectors, which we refer to as Task Singular Vectors (TSV). Recognizing that layer task matrices are often low-rank, we propose TSV-Compress (TSV-C), a simple procedure that compresses them to 10% of their original size while retaining 99% of accuracy. We further leverage this low-rank space to define a new measure of task interference based on the interaction of singular vectors from different tasks. Building on these findings, we introduce TSV-Merge (TSV-M), a novel model merging approach that combines compression with interference reduction, significantly outperforming existing methods.

ATM: Improving Model Merging by Alternating Tuning and Merging

Model merging has recently emerged as a cost-efficient paradigm for multi-task learning. Among current approaches, task arithmetic stands out for its simplicity and effectiveness. In this paper, we motivate the effectiveness of task vectors by linking them to multi-task gradients. We show that in a single-epoch scenario, task vectors are mathematically equivalent to the gradients obtained via gradient descent in a multi-task setting, and still approximate these gradients in subsequent epochs. Furthermore, we show that task vectors perform optimally when equality is maintained, and their effectiveness is largely driven by the first epoch's gradient. Building on this insight, we propose viewing model merging as a single step in an iterative process that Alternates between Tuning and Merging (ATM). This method acts as a bridge between model merging and multi-task gradient descent, achieving state-of-the-art results with the same data and computational requirements. We extensively evaluate ATM across diverse settings, achieving up to 20% higher accuracy in computer vision and NLP tasks, compared to the best baselines.Finally, we provide both empirical and theoretical support for its effectiveness, demonstrating increased orthogonality between task vectors and proving that ATM minimizes an upper bound on the loss obtained by jointly finetuning all tasks.

$C^2M^3$: Cycle-Consistent Multi-Model Merging

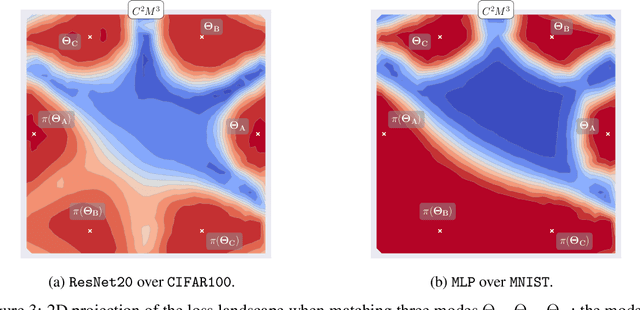
In this paper, we present a novel data-free method for merging neural networks in weight space. Differently from most existing works, our method optimizes for the permutations of network neurons globally across all layers. This allows us to enforce cycle consistency of the permutations when merging $N \geq 3$ models, allowing circular compositions of permutations to be computed without accumulating error along the path. We qualitatively and quantitatively motivate the need for such a constraint, showing its benefits when merging sets of models in scenarios spanning varying architectures and datasets. We finally show that, when coupled with activation renormalization, our approach yields the best results in the task.