Look Around and Find Out: OOD Detection with Relative Angles

Deep learning systems deployed in real-world applications often encounter data that is different from their in-distribution (ID). A reliable system should ideally abstain from making decisions in this out-of-distribution (OOD) setting. Existing state-of-the-art methods primarily focus on feature distances, such as k-th nearest neighbors and distances to decision boundaries, either overlooking or ineffectively using in-distribution statistics. In this work, we propose a novel angle-based metric for OOD detection that is computed relative to the in-distribution structure. We demonstrate that the angles between feature representations and decision boundaries, viewed from the mean of in-distribution features, serve as an effective discriminative factor between ID and OOD data. Our method achieves state-of-the-art performance on CIFAR-10 and ImageNet benchmarks, reducing FPR95 by 0.88% and 7.74% respectively. Our score function is compatible with existing feature space regularization techniques, enhancing performance. Additionally, its scale-invariance property enables creating an ensemble of models for OOD detection via simple score summation.

Unifying Causal Representation Learning with the Invariance Principle

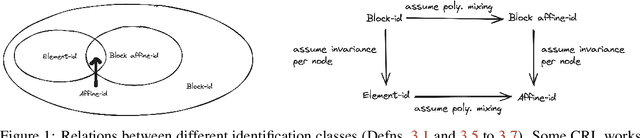
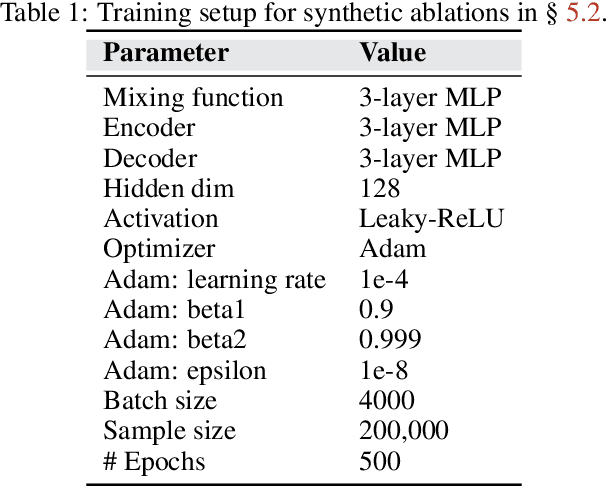
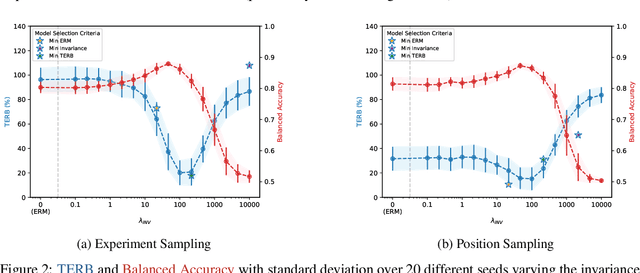
Causal representation learning aims at recovering latent causal variables from high-dimensional observations to solve causal downstream tasks, such as predicting the effect of new interventions or more robust classification. A plethora of methods have been developed, each tackling carefully crafted problem settings that lead to different types of identifiability. The folklore is that these different settings are important, as they are often linked to different rungs of Pearl's causal hierarchy, although not all neatly fit. Our main contribution is to show that many existing causal representation learning approaches methodologically align the representation to known data symmetries. Identification of the variables is guided by equivalence classes across different data pockets that are not necessarily causal. This result suggests important implications, allowing us to unify many existing approaches in a single method that can mix and match different assumptions, including non-causal ones, based on the invariances relevant to our application. It also significantly benefits applicability, which we demonstrate by improving treatment effect estimation on real-world high-dimensional ecological data. Overall, this paper clarifies the role of causality assumptions in the discovery of causal variables and shifts the focus to preserving data symmetries.

Latent Space Translation via Inverse Relative Projection

The emergence of similar representations between independently trained neural models has sparked significant interest in the representation learning community, leading to the development of various methods to obtain communication between latent spaces. "Latent space communication" can be achieved in two ways: i) by independently mapping the original spaces to a shared or relative one; ii) by directly estimating a transformation from a source latent space to a target one. In this work, we combine the two into a novel method to obtain latent space translation through the relative space. By formalizing the invertibility of angle-preserving relative representations and assuming the scale invariance of decoder modules in neural models, we can effectively use the relative space as an intermediary, independently projecting onto and from other semantically similar spaces. Extensive experiments over various architectures and datasets validate our scale invariance assumption and demonstrate the high accuracy of our method in latent space translation. We also apply our method to zero-shot stitching between arbitrary pre-trained text and image encoders and their classifiers, even across modalities. Our method has significant potential for facilitating the reuse of models in a practical manner via compositionality.

Latent Functional Maps

Neural models learn data representations that lie on low-dimensional manifolds, yet modeling the relation between these representational spaces is an ongoing challenge. By integrating spectral geometry principles into neural modeling, we show that this problem can be better addressed in the functional domain, mitigating complexity, while enhancing interpretability and performances on downstream tasks. To this end, we introduce a multi-purpose framework to the representation learning community, which allows to: (i) compare different spaces in an interpretable way and measure their intrinsic similarity; (ii) find correspondences between them, both in unsupervised and weakly supervised settings, and (iii) to effectively transfer representations between distinct spaces. We validate our framework on various applications, ranging from stitching to retrieval tasks, demonstrating that latent functional maps can serve as a swiss-army knife for representation alignment.

Latent. Functional Map

Neural models learn data representations that lie on low-dimensional manifolds, yet modeling the relation between these representational spaces is an ongoing challenge. By integrating spectral geometry principles into neural modeling, we show that this problem can be better addressed in the functional domain, mitigating complexity, while enhancing interpretability and performances on downstream tasks. To this end, we introduce a multi-purpose framework to the representation learning community, which allows to: (i) compare different spaces in an interpretable way and measure their intrinsic similarity; (ii) find correspondences between them, both in unsupervised and weakly supervised settings, and (iii) to effectively transfer representations between distinct spaces. We validate our framework on various applications, ranging from stitching to retrieval tasks, demonstrating that latent functional maps can serve as a swiss-army knife for representation alignment.

$C^2M^3$: Cycle-Consistent Multi-Model Merging

In this paper, we present a novel data-free method for merging neural networks in weight space. Differently from most existing works, our method optimizes for the permutations of network neurons globally across all layers. This allows us to enforce cycle consistency of the permutations when merging $N \geq 3$ models, allowing circular compositions of permutations to be computed without accumulating error along the path. We qualitatively and quantitatively motivate the need for such a constraint, showing its benefits when merging sets of models in scenarios spanning varying architectures and datasets. We finally show that, when coupled with activation renormalization, our approach yields the best results in the task.

Latent Space Translation via Semantic Alignment

While different neural models often exhibit latent spaces that are alike when exposed to semantically related data, this intrinsic similarity is not always immediately discernible. Towards a better understanding of this phenomenon, our work shows how representations learned from these neural modules can be translated between different pre-trained networks via simpler transformations than previously thought. An advantage of this approach is the ability to estimate these transformations using standard, well-understood algebraic procedures that have closed-form solutions. Our method directly estimates a transformation between two given latent spaces, thereby enabling effective stitching of encoders and decoders without additional training. We extensively validate the adaptability of this translation procedure in different experimental settings: across various trainings, domains, architectures (e.g., ResNet, CNN, ViT), and in multiple downstream tasks (classification, reconstruction). Notably, we show how it is possible to zero-shot stitch text encoders and vision decoders, or vice-versa, yielding surprisingly good classification performance in this multimodal setting.

From Bricks to Bridges: Product of Invariances to Enhance Latent Space Communication

It has been observed that representations learned by distinct neural networks conceal structural similarities when the models are trained under similar inductive biases. From a geometric perspective, identifying the classes of transformations and the related invariances that connect these representations is fundamental to unlocking applications, such as merging, stitching, and reusing different neural modules. However, estimating task-specific transformations a priori can be challenging and expensive due to several factors (e.g., weights initialization, training hyperparameters, or data modality). To this end, we introduce a versatile method to directly incorporate a set of invariances into the representations, constructing a product space of invariant components on top of the latent representations without requiring prior knowledge about the optimal invariance to infuse. We validate our solution on classification and reconstruction tasks, observing consistent latent similarity and downstream performance improvements in a zero-shot stitching setting. The experimental analysis comprises three modalities (vision, text, and graphs), twelve pretrained foundational models, eight benchmarks, and several architectures trained from scratch.

Leveraging sparse and shared feature activations for disentangled representation learning

Recovering the latent factors of variation of high dimensional data has so far focused on simple synthetic settings. Mostly building on unsupervised and weakly-supervised objectives, prior work missed out on the positive implications for representation learning on real world data. In this work, we propose to leverage knowledge extracted from a diversified set of supervised tasks to learn a common disentangled representation. Assuming each supervised task only depends on an unknown subset of the factors of variation, we disentangle the feature space of a supervised multi-task model, with features activating sparsely across different tasks and information being shared as appropriate. Importantly, we never directly observe the factors of variations but establish that access to multiple tasks is sufficient for identifiability under sufficiency and minimality assumptions. We validate our approach on six real world distribution shift benchmarks, and different data modalities (images, text), demonstrating how disentangled representations can be transferred to real settings.

Bootstrapping Parallel Anchors for Relative Representations

The use of relative representations for latent embeddings has shown potential in enabling latent space communication and zero-shot model stitching across a wide range of applications. Nevertheless, relative representations rely on a certain amount of parallel anchors to be given as input, which can be impractical to obtain in certain scenarios. To overcome this limitation, we propose an optimization-based method to discover new parallel anchors from a limited number of seeds. Our approach can be used to find semantic correspondence between different domains, align their relative spaces, and achieve competitive results in several tasks.