Scalable Mechanistic Neural Networks

We propose Scalable Mechanistic Neural Network (S-MNN), an enhanced neural network framework designed for scientific machine learning applications involving long temporal sequences. By reformulating the original Mechanistic Neural Network (MNN) (Pervez et al., 2024), we reduce the computational time and space complexities from cubic and quadratic with respect to the sequence length, respectively, to linear. This significant improvement enables efficient modeling of long-term dynamics without sacrificing accuracy or interpretability. Extensive experiments demonstrate that S-MNN matches the original MNN in precision while substantially reducing computational resources. Consequently, S-MNN can drop-in replace the original MNN in applications, providing a practical and efficient tool for integrating mechanistic bottlenecks into neural network models of complex dynamical systems.

Unifying Causal Representation Learning with the Invariance Principle

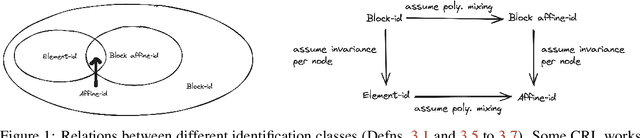
Causal representation learning aims at recovering latent causal variables from high-dimensional observations to solve causal downstream tasks, such as predicting the effect of new interventions or more robust classification. A plethora of methods have been developed, each tackling carefully crafted problem settings that lead to different types of identifiability. The folklore is that these different settings are important, as they are often linked to different rungs of Pearl's causal hierarchy, although not all neatly fit. Our main contribution is to show that many existing causal representation learning approaches methodologically align the representation to known data symmetries. Identification of the variables is guided by equivalence classes across different data pockets that are not necessarily causal. This result suggests important implications, allowing us to unify many existing approaches in a single method that can mix and match different assumptions, including non-causal ones, based on the invariances relevant to our application. It also significantly benefits applicability, which we demonstrate by improving treatment effect estimation on real-world high-dimensional ecological data. Overall, this paper clarifies the role of causality assumptions in the discovery of causal variables and shifts the focus to preserving data symmetries.

Marrying Causal Representation Learning with Dynamical Systems for Science

Causal representation learning promises to extend causal models to hidden causal variables from raw entangled measurements. However, most progress has focused on proving identifiability results in different settings, and we are not aware of any successful real-world application. At the same time, the field of dynamical systems benefited from deep learning and scaled to countless applications but does not allow parameter identification. In this paper, we draw a clear connection between the two and their key assumptions, allowing us to apply identifiable methods developed in causal representation learning to dynamical systems. At the same time, we can leverage scalable differentiable solvers developed for differential equations to build models that are both identifiable and practical. Overall, we learn explicitly controllable models that isolate the trajectory-specific parameters for further downstream tasks such as out-of-distribution classification or treatment effect estimation. We experiment with a wind simulator with partially known factors of variation. We also apply the resulting model to real-world climate data and successfully answer downstream causal questions in line with existing literature on climate change.

A Sparsity Principle for Partially Observable Causal Representation Learning

Causal representation learning aims at identifying high-level causal variables from perceptual data. Most methods assume that all latent causal variables are captured in the high-dimensional observations. We instead consider a partially observed setting, in which each measurement only provides information about a subset of the underlying causal state. Prior work has studied this setting with multiple domains or views, each depending on a fixed subset of latents. Here, we focus on learning from unpaired observations from a dataset with an instance-dependent partial observability pattern. Our main contribution is to establish two identifiability results for this setting: one for linear mixing functions without parametric assumptions on the underlying causal model, and one for piecewise linear mixing functions with Gaussian latent causal variables. Based on these insights, we propose two methods for estimating the underlying causal variables by enforcing sparsity in the inferred representation. Experiments on different simulated datasets and established benchmarks highlight the effectiveness of our approach in recovering the ground-truth latents.

Multi-View Causal Representation Learning with Partial Observability

We present a unified framework for studying the identifiability of representations learned from simultaneously observed views, such as different data modalities. We allow a partially observed setting in which each view constitutes a nonlinear mixture of a subset of underlying latent variables, which can be causally related. We prove that the information shared across all subsets of any number of views can be learned up to a smooth bijection using contrastive learning and a single encoder per view. We also provide graphical criteria indicating which latent variables can be identified through a simple set of rules, which we refer to as identifiability algebra. Our general framework and theoretical results unify and extend several previous works on multi-view nonlinear ICA, disentanglement, and causal representation learning. We experimentally validate our claims on numerical, image, and multi-modal data sets. Further, we demonstrate that the performance of prior methods is recovered in different special cases of our setup. Overall, we find that access to multiple partial views enables us to identify a more fine-grained representation, under the generally milder assumption of partial observability.

Active Learning in Gaussian Process State Space Model

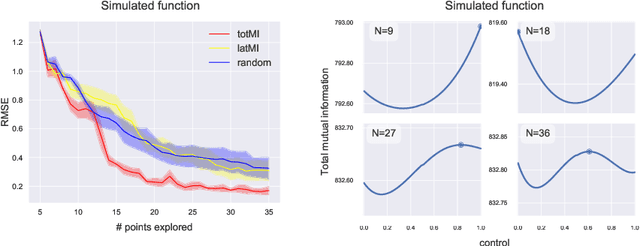
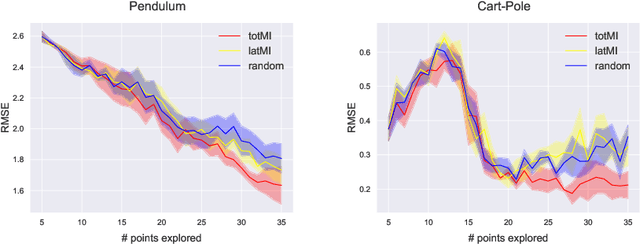
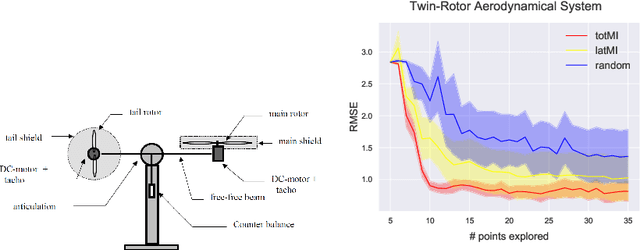
We investigate active learning in Gaussian Process state-space models (GPSSM). Our problem is to actively steer the system through latent states by determining its inputs such that the underlying dynamics can be optimally learned by a GPSSM. In order that the most informative inputs are selected, we employ mutual information as our active learning criterion. In particular, we present two approaches for the approximation of mutual information for the GPSSM given latent states. The proposed approaches are evaluated in several physical systems where we actively learn the underlying non-linear dynamics represented by the state-space model.