Mechanistic PDE Networks for Discovery of Governing Equations

We present Mechanistic PDE Networks -- a model for discovery of governing partial differential equations from data. Mechanistic PDE Networks represent spatiotemporal data as space-time dependent linear partial differential equations in neural network hidden representations. The represented PDEs are then solved and decoded for specific tasks. The learned PDE representations naturally express the spatiotemporal dynamics in data in neural network hidden space, enabling increased power for dynamical modeling. Solving the PDE representations in a compute and memory-efficient way, however, is a significant challenge. We develop a native, GPU-capable, parallel, sparse, and differentiable multigrid solver specialized for linear partial differential equations that acts as a module in Mechanistic PDE Networks. Leveraging the PDE solver, we propose a discovery architecture that can discover nonlinear PDEs in complex settings while also being robust to noise. We validate PDE discovery on a number of PDEs, including reaction-diffusion and Navier-Stokes equations.

Scalable Mechanistic Neural Networks

We propose Scalable Mechanistic Neural Network (S-MNN), an enhanced neural network framework designed for scientific machine learning applications involving long temporal sequences. By reformulating the original Mechanistic Neural Network (MNN) (Pervez et al., 2024), we reduce the computational time and space complexities from cubic and quadratic with respect to the sequence length, respectively, to linear. This significant improvement enables efficient modeling of long-term dynamics without sacrificing accuracy or interpretability. Extensive experiments demonstrate that S-MNN matches the original MNN in precision while substantially reducing computational resources. Consequently, S-MNN can drop-in replace the original MNN in applications, providing a practical and efficient tool for integrating mechanistic bottlenecks into neural network models of complex dynamical systems.

Mechanistic Neural Networks for Scientific Machine Learning

This paper presents Mechanistic Neural Networks, a neural network design for machine learning applications in the sciences. It incorporates a new Mechanistic Block in standard architectures to explicitly learn governing differential equations as representations, revealing the underlying dynamics of data and enhancing interpretability and efficiency in data modeling. Central to our approach is a novel Relaxed Linear Programming Solver (NeuRLP) inspired by a technique that reduces solving linear ODEs to solving linear programs. This integrates well with neural networks and surpasses the limitations of traditional ODE solvers enabling scalable GPU parallel processing. Overall, Mechanistic Neural Networks demonstrate their versatility for scientific machine learning applications, adeptly managing tasks from equation discovery to dynamic systems modeling. We prove their comprehensive capabilities in analyzing and interpreting complex scientific data across various applications, showing significant performance against specialized state-of-the-art methods.

Differentiable Mathematical Programming for Object-Centric Representation Learning

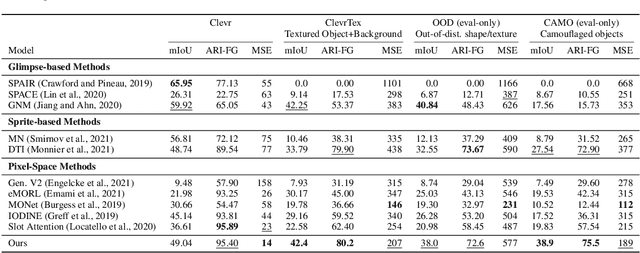
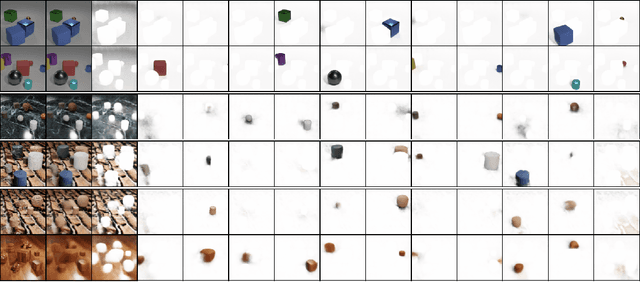
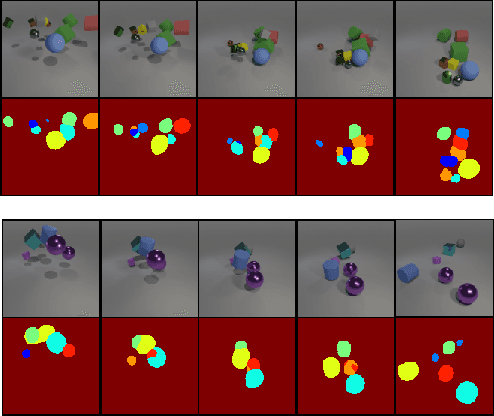
We propose topology-aware feature partitioning into $k$ disjoint partitions for given scene features as a method for object-centric representation learning. To this end, we propose to use minimum $s$-$t$ graph cuts as a partitioning method which is represented as a linear program. The method is topologically aware since it explicitly encodes neighborhood relationships in the image graph. To solve the graph cuts our solution relies on an efficient, scalable, and differentiable quadratic programming approximation. Optimizations specific to cut problems allow us to solve the quadratic programs and compute their gradients significantly more efficiently compared with the general quadratic programming approach. Our results show that our approach is scalable and outperforms existing methods on object discovery tasks with textured scenes and objects.

A Fourier View of REINFORCE

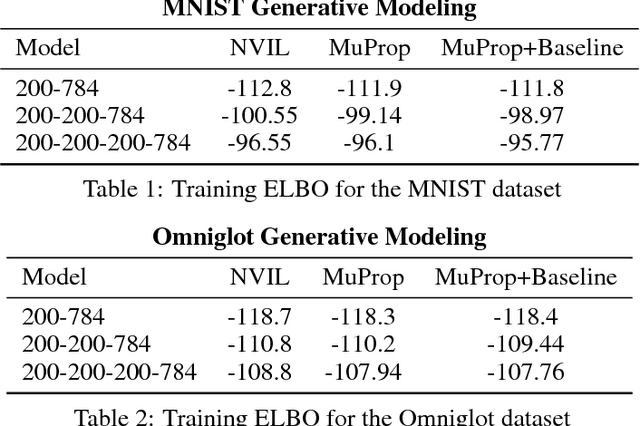
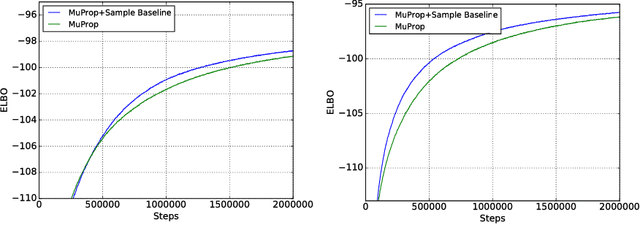
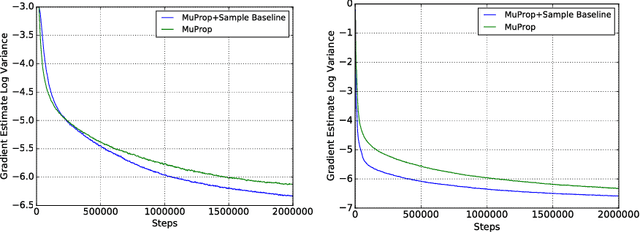
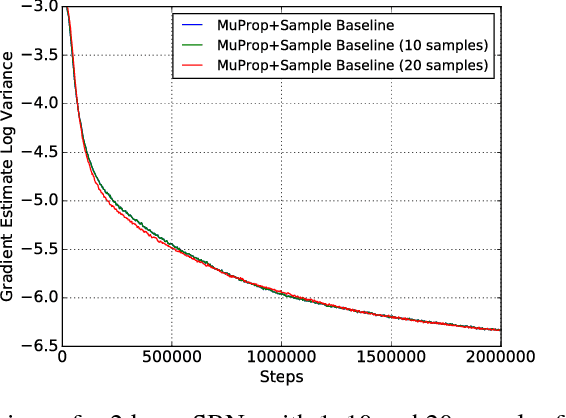
We show a connection between the Fourier spectrum of Boolean functions and the REINFORCE gradient estimator for binary latent variable models. We show that REINFORCE estimates (up to a factor) the degree-1 Fourier coefficients of a Boolean function. Using this connection we offer a new perspective on variance reduction in gradient estimation for latent variable models: namely, that variance reduction involves eliminating or reducing Fourier coefficients that do not have degree 1. We then use this connection to develop low-variance unbiased gradient estimators for binary latent variable models such as sigmoid belief networks. The estimator is based upon properties of the noise operator from Boolean Fourier theory and involves a sample-dependent baseline added to the REINFORCE estimator in a way that keeps the estimator unbiased. The baseline can be plugged into existing gradient estimators for further variance reduction.