A Fourier View of REINFORCE
Paper and Code
Aug 12, 2018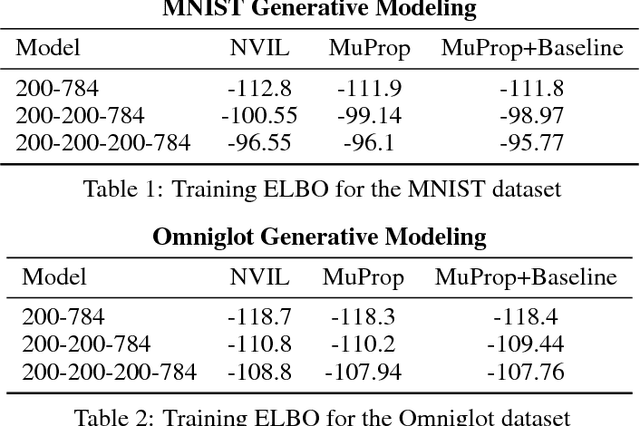
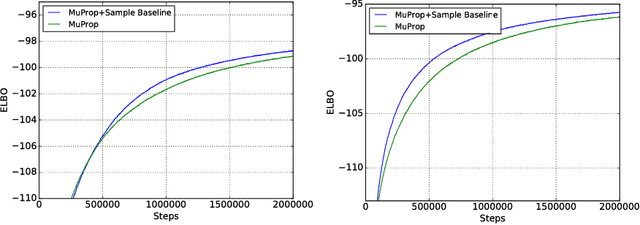
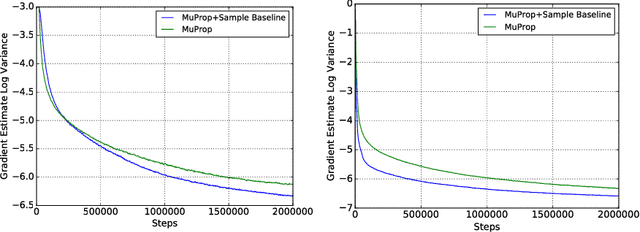
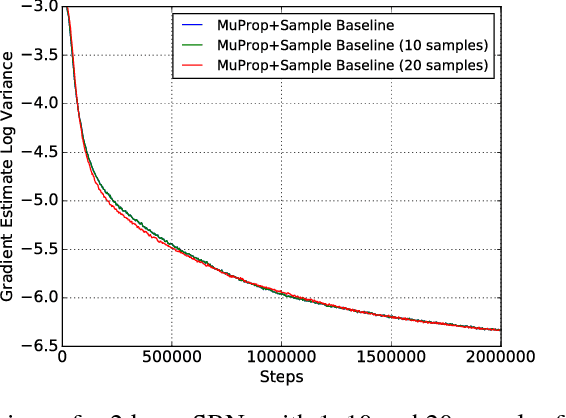
We show a connection between the Fourier spectrum of Boolean functions and the REINFORCE gradient estimator for binary latent variable models. We show that REINFORCE estimates (up to a factor) the degree-1 Fourier coefficients of a Boolean function. Using this connection we offer a new perspective on variance reduction in gradient estimation for latent variable models: namely, that variance reduction involves eliminating or reducing Fourier coefficients that do not have degree 1. We then use this connection to develop low-variance unbiased gradient estimators for binary latent variable models such as sigmoid belief networks. The estimator is based upon properties of the noise operator from Boolean Fourier theory and involves a sample-dependent baseline added to the REINFORCE estimator in a way that keeps the estimator unbiased. The baseline can be plugged into existing gradient estimators for further variance reduction.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge