Batch Active Learning in Gaussian Process Regression using Derivatives

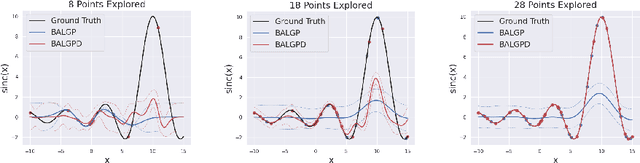
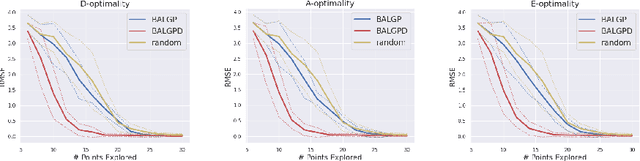
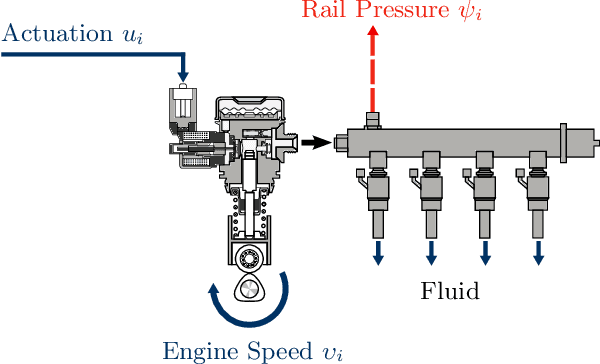
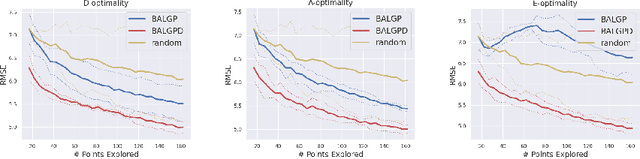
We investigate the use of derivative information for Batch Active Learning in Gaussian Process regression models. The proposed approach employs the predictive covariance matrix for selection of data batches to exploit full correlation of samples. We theoretically analyse our proposed algorithm taking different optimality criteria into consideration and provide empirical comparisons highlighting the advantage of incorporating derivatives information. Our results show the effectiveness of our approach across diverse applications.

Active Learning in Gaussian Process State Space Model

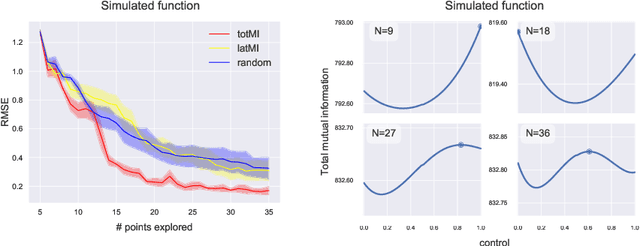
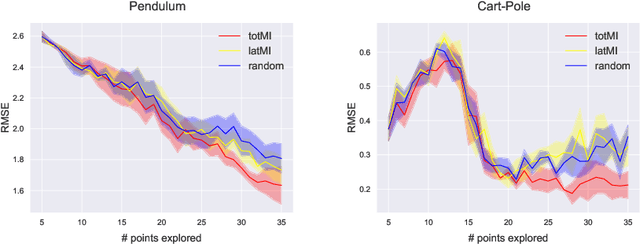
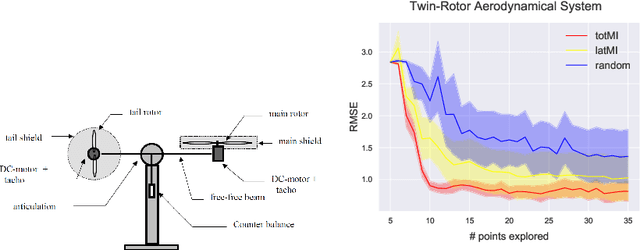
We investigate active learning in Gaussian Process state-space models (GPSSM). Our problem is to actively steer the system through latent states by determining its inputs such that the underlying dynamics can be optimally learned by a GPSSM. In order that the most informative inputs are selected, we employ mutual information as our active learning criterion. In particular, we present two approaches for the approximation of mutual information for the GPSSM given latent states. The proposed approaches are evaluated in several physical systems where we actively learn the underlying non-linear dynamics represented by the state-space model.