Batch Active Learning in Gaussian Process Regression using Derivatives

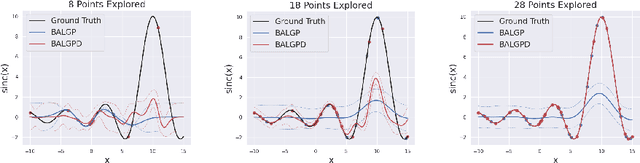
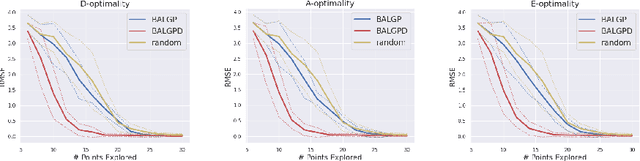
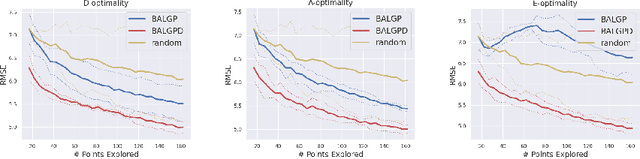
We investigate the use of derivative information for Batch Active Learning in Gaussian Process regression models. The proposed approach employs the predictive covariance matrix for selection of data batches to exploit full correlation of samples. We theoretically analyse our proposed algorithm taking different optimality criteria into consideration and provide empirical comparisons highlighting the advantage of incorporating derivatives information. Our results show the effectiveness of our approach across diverse applications.

Safe Active Learning for Time-Series Modeling with Gaussian Processes

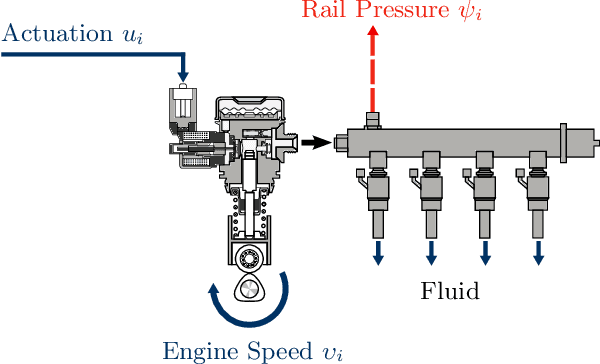
Learning time-series models is useful for many applications, such as simulation and forecasting. In this study, we consider the problem of actively learning time-series models while taking given safety constraints into account. For time-series modeling we employ a Gaussian process with a nonlinear exogenous input structure. The proposed approach generates data appropriate for time series model learning, i.e. input and output trajectories, by dynamically exploring the input space. The approach parametrizes the input trajectory as consecutive trajectory sections, which are determined stepwise given safety requirements and past observations. We analyze the proposed algorithm and evaluate it empirically on a technical application. The results show the effectiveness of our approach in a realistic technical use case.

Active Learning in Gaussian Process State Space Model

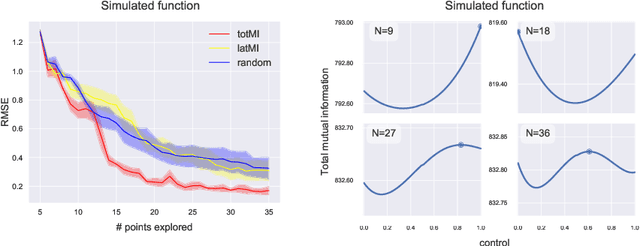
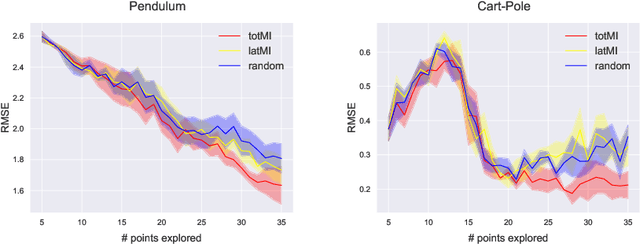
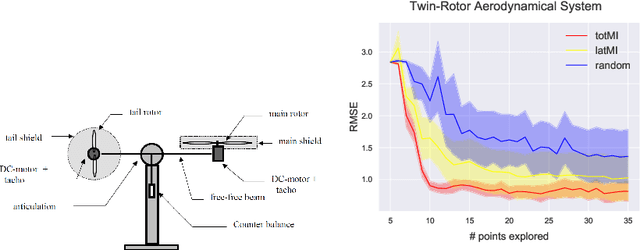
We investigate active learning in Gaussian Process state-space models (GPSSM). Our problem is to actively steer the system through latent states by determining its inputs such that the underlying dynamics can be optimally learned by a GPSSM. In order that the most informative inputs are selected, we employ mutual information as our active learning criterion. In particular, we present two approaches for the approximation of mutual information for the GPSSM given latent states. The proposed approaches are evaluated in several physical systems where we actively learn the underlying non-linear dynamics represented by the state-space model.

Probabilistic Recurrent State-Space Models

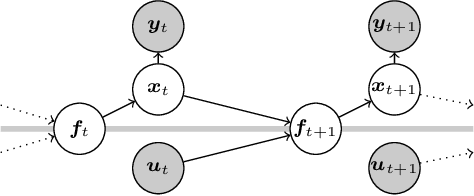
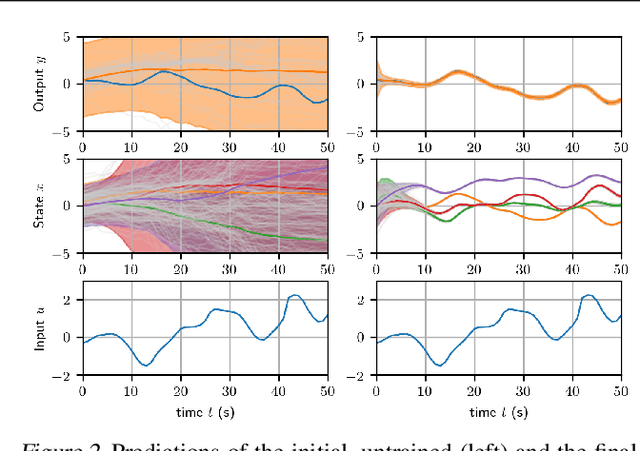
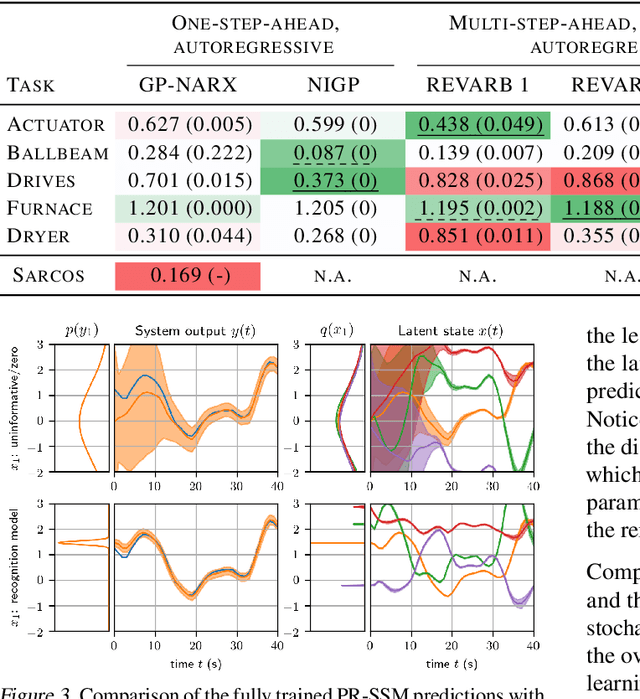
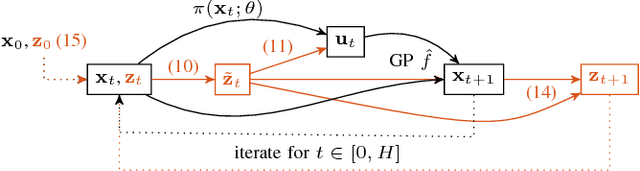
State-space models (SSMs) are a highly expressive model class for learning patterns in time series data and for system identification. Deterministic versions of SSMs (e.g. LSTMs) proved extremely successful in modeling complex time series data. Fully probabilistic SSMs, however, are often found hard to train, even for smaller problems. To overcome this limitation, we propose a novel model formulation and a scalable training algorithm based on doubly stochastic variational inference and Gaussian processes. In contrast to existing work, the proposed variational approximation allows one to fully capture the latent state temporal correlations. These correlations are the key to robust training. The effectiveness of the proposed PR-SSM is evaluated on a set of real-world benchmark datasets in comparison to state-of-the-art probabilistic model learning methods. Scalability and robustness are demonstrated on a high dimensional problem.

Model-Based Policy Search for Automatic Tuning of Multivariate PID Controllers

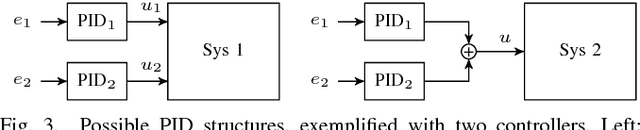
PID control architectures are widely used in industrial applications. Despite their low number of open parameters, tuning multiple, coupled PID controllers can become tedious in practice. In this paper, we extend PILCO, a model-based policy search framework, to automatically tune multivariate PID controllers purely based on data observed on an otherwise unknown system. The system's state is extended appropriately to frame the PID policy as a static state feedback policy. This renders PID tuning possible as the solution of a finite horizon optimal control problem without further a priori knowledge. The framework is applied to the task of balancing an inverted pendulum on a seven degree-of-freedom robotic arm, thereby demonstrating its capabilities of fast and data-efficient policy learning, even on complex real world problems.