Differentiable Likelihoods for Fast Inversion of 'Likelihood-Free' Dynamical Systems

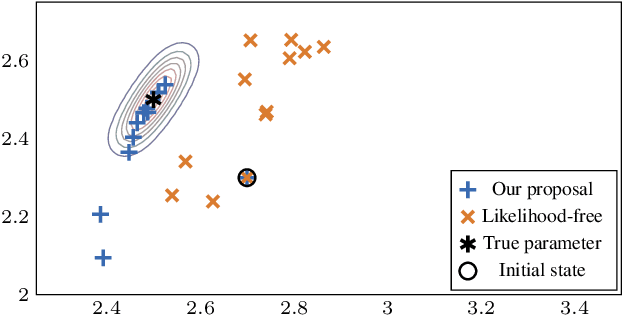
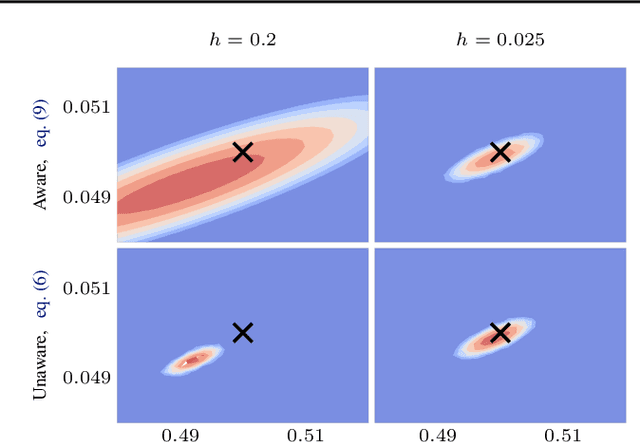
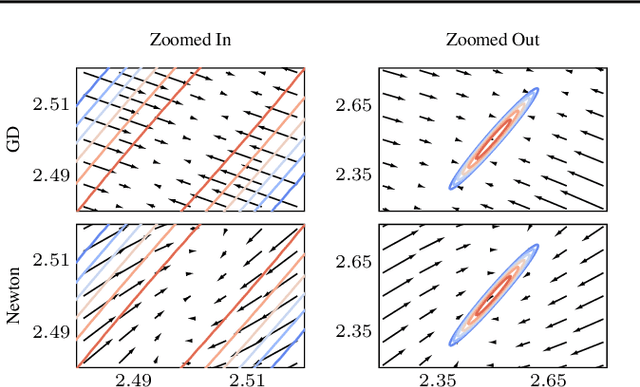
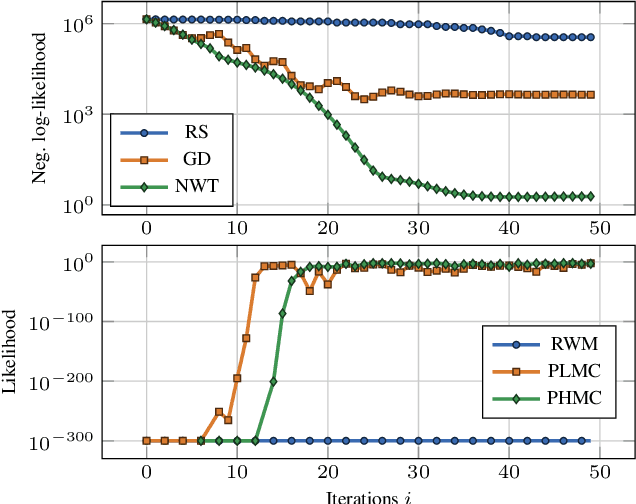
Likelihood-free (a.k.a. simulation-based) inference problems are inverse problems with expensive, or intractable, forward models. ODE inverse problems are commonly treated as likelihood-free, as their forward map has to be numerically approximated by an ODE solver. This, however, is not a fundamental constraint but just a lack of functionality in classic ODE solvers, which do not return a likelihood but a point estimate. To address this shortcoming, we employ Gaussian ODE filtering (a probabilistic numerical method for ODEs) to construct a local Gaussian approximation to the likelihood. This approximation yields tractable estimators for the gradient and Hessian of the (log-)likelihood. Insertion of these estimators into existing gradient-based optimization and sampling methods engenders new solvers for ODE inverse problems. We demonstrate that these methods outperform standard likelihood-free approaches on three benchmark-systems.

Relational Generalized Few-Shot Learning

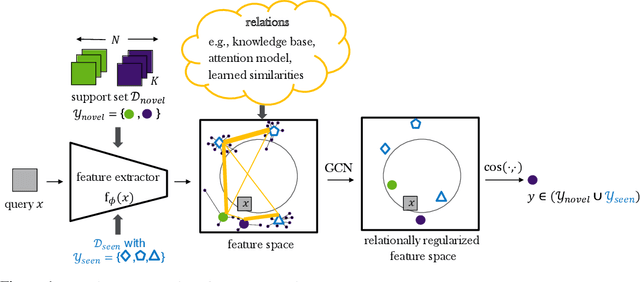
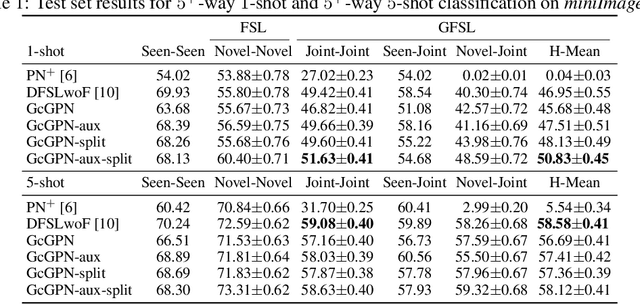
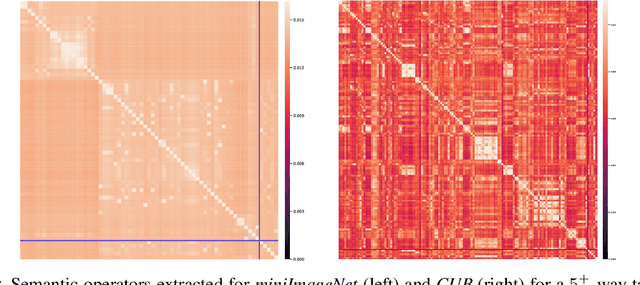
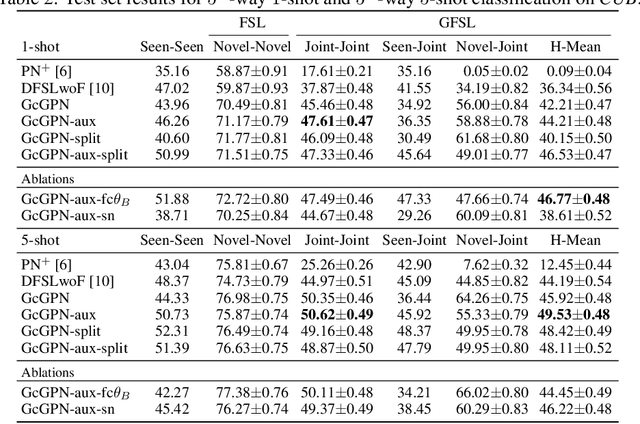
Transferring learned models to novel tasks is a challenging problem, particularly if only very few labeled examples are available. Although this few-shot learning setup has received a lot of attention recently, most proposed methods focus on discriminating novel classes only. Instead, we consider the extended setup of generalized few-shot learning (GFSL), where the model is required to perform classification on the joint label space consisting of both previously seen and novel classes. We propose a graph-based framework that explicitly models relationships between all seen and novel classes in the joint label space. Our model Graph-convolutional Global Prototypical Networks (GcGPN) incorporates these inter-class relations using graph-convolution in order to embed novel class representations into the existing space of previously seen classes in a globally consistent manner. Our approach ensures both fast adaptation and global discrimination, which is the major challenge in GFSL. We demonstrate the benefits of our model on two challenging benchmark datasets.

Probabilistic Recurrent State-Space Models

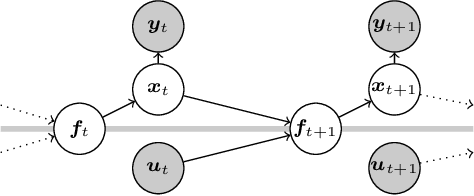
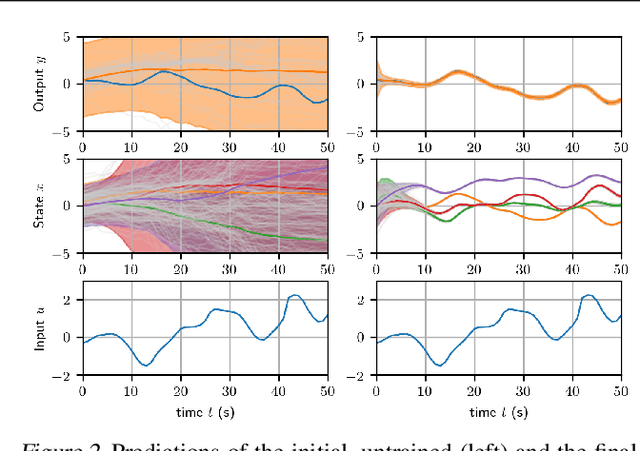
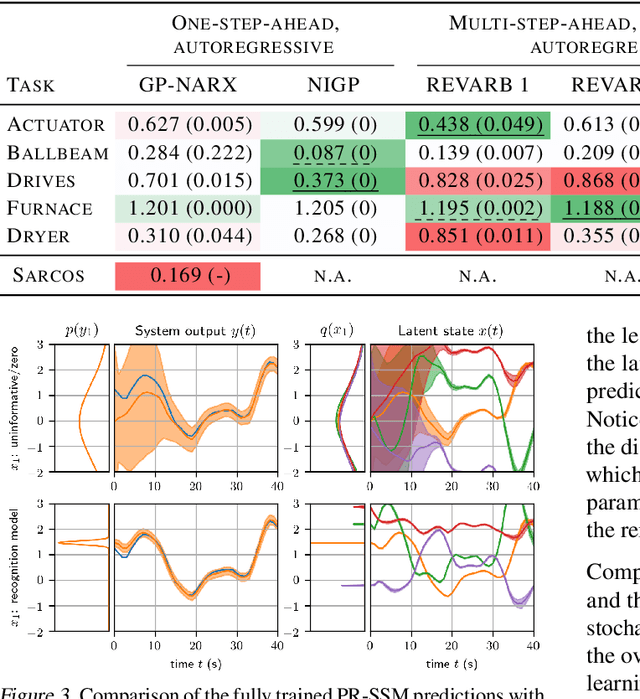
State-space models (SSMs) are a highly expressive model class for learning patterns in time series data and for system identification. Deterministic versions of SSMs (e.g. LSTMs) proved extremely successful in modeling complex time series data. Fully probabilistic SSMs, however, are often found hard to train, even for smaller problems. To overcome this limitation, we propose a novel model formulation and a scalable training algorithm based on doubly stochastic variational inference and Gaussian processes. In contrast to existing work, the proposed variational approximation allows one to fully capture the latent state temporal correlations. These correlations are the key to robust training. The effectiveness of the proposed PR-SSM is evaluated on a set of real-world benchmark datasets in comparison to state-of-the-art probabilistic model learning methods. Scalability and robustness are demonstrated on a high dimensional problem.