SOLO: Search Online, Learn Offline for Combinatorial Optimization Problems

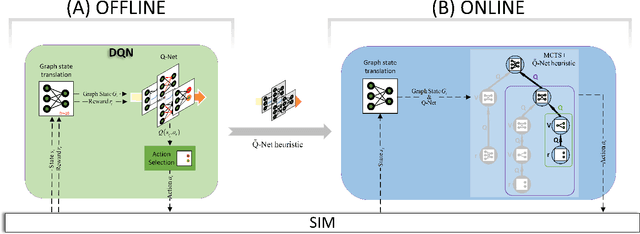
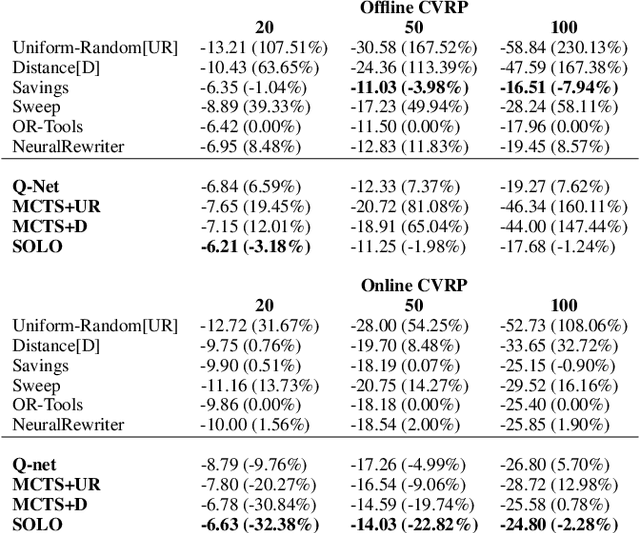
We study combinatorial problems with real world applications such as machine scheduling, routing, and assignment. We propose a method that combines Reinforcement Learning (RL) and planning. This method can equally be applied to both the offline, as well as online, variants of the combinatorial problem, in which the problem components (e.g., jobs in scheduling problems) are not known in advance, but rather arrive during the decision-making process. Our solution is quite generic, scalable, and leverages distributional knowledge of the problem parameters. We frame the solution process as an MDP, and take a Deep Q-Learning approach wherein states are represented as graphs, thereby allowing our trained policies to deal with arbitrary changes in a principled manner. Though learned policies work well in expectation, small deviations can have substantial negative effects in combinatorial settings. We mitigate these drawbacks by employing our graph-convolutional policies as non-optimal heuristics in a compatible search algorithm, Monte Carlo Tree Search, to significantly improve overall performance. We demonstrate our method on two problems: Machine Scheduling and Capacitated Vehicle Routing. We show that our method outperforms custom-tailored mathematical solvers, state of the art learning-based algorithms, and common heuristics, both in computation time and performance.

Differentiable Likelihoods for Fast Inversion of 'Likelihood-Free' Dynamical Systems

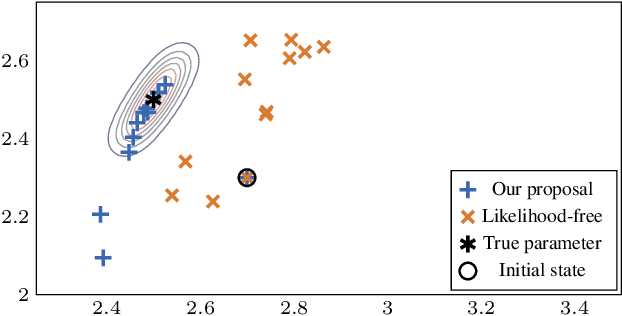
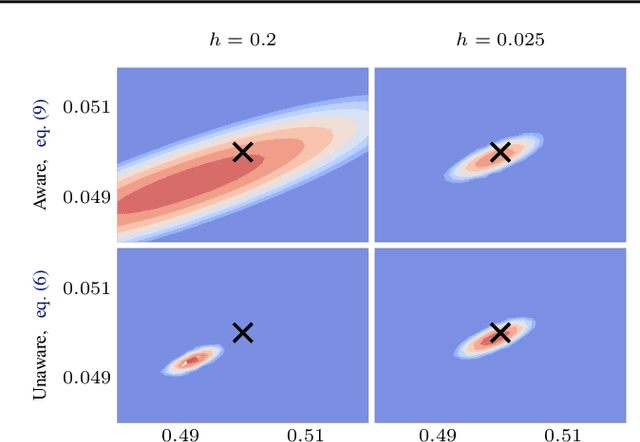
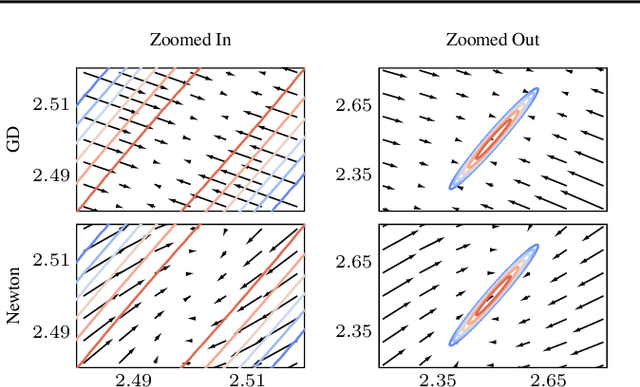
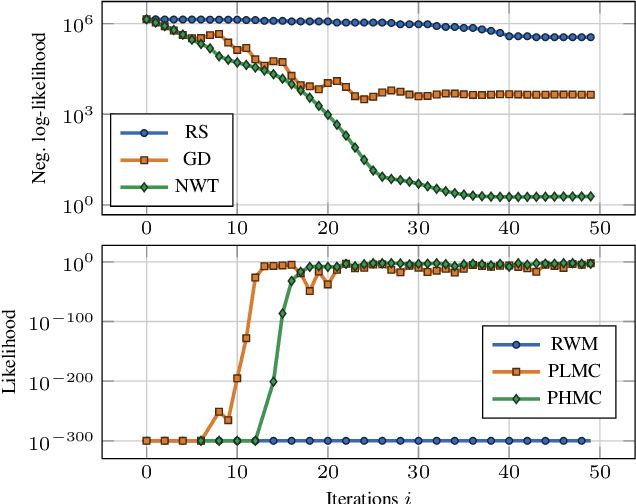
Likelihood-free (a.k.a. simulation-based) inference problems are inverse problems with expensive, or intractable, forward models. ODE inverse problems are commonly treated as likelihood-free, as their forward map has to be numerically approximated by an ODE solver. This, however, is not a fundamental constraint but just a lack of functionality in classic ODE solvers, which do not return a likelihood but a point estimate. To address this shortcoming, we employ Gaussian ODE filtering (a probabilistic numerical method for ODEs) to construct a local Gaussian approximation to the likelihood. This approximation yields tractable estimators for the gradient and Hessian of the (log-)likelihood. Insertion of these estimators into existing gradient-based optimization and sampling methods engenders new solvers for ODE inverse problems. We demonstrate that these methods outperform standard likelihood-free approaches on three benchmark-systems.

Noisy-Input Entropy Search for Efficient Robust Bayesian Optimization

We consider the problem of robust optimization within the well-established Bayesian optimization (BO) framework. While BO is intrinsically robust to noisy evaluations of the objective function, standard approaches do not consider the case of uncertainty about the input parameters. In this paper, we propose Noisy-Input Entropy Search (NES), a novel information-theoretic acquisition function that is designed to find robust optima for problems with both input and measurement noise. NES is based on the key insight that the robust objective in many cases can be modeled as a Gaussian process, however, it cannot be observed directly. We evaluate NES on several benchmark problems from the optimization literature and from engineering. The results show that NES reliably finds robust optima, outperforming existing methods from the literature on all benchmarks.

Trajectory-Based Off-Policy Deep Reinforcement Learning

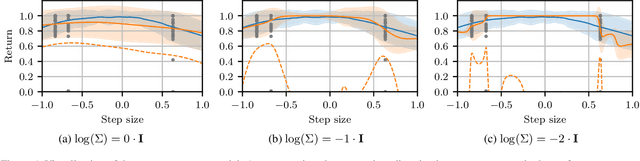
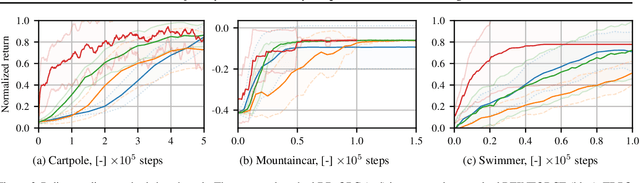
Policy gradient methods are powerful reinforcement learning algorithms and have been demonstrated to solve many complex tasks. However, these methods are also data-inefficient, afflicted with high variance gradient estimates, and frequently get stuck in local optima. This work addresses these weaknesses by combining recent improvements in the reuse of off-policy data and exploration in parameter space with deterministic behavioral policies. The resulting objective is amenable to standard neural network optimization strategies like stochastic gradient descent or stochastic gradient Hamiltonian Monte Carlo. Incorporation of previous rollouts via importance sampling greatly improves data-efficiency, whilst stochastic optimization schemes facilitate the escape from local optima. We evaluate the proposed approach on a series of continuous control benchmark tasks. The results show that the proposed algorithm is able to successfully and reliably learn solutions using fewer system interactions than standard policy gradient methods.

Meta-Learning Acquisition Functions for Bayesian Optimization

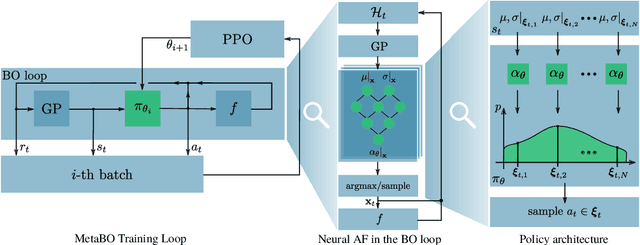
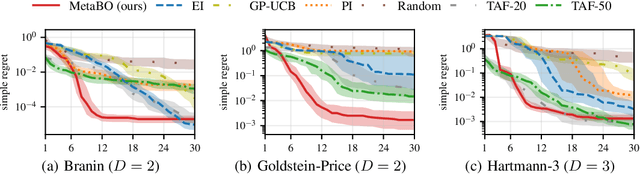
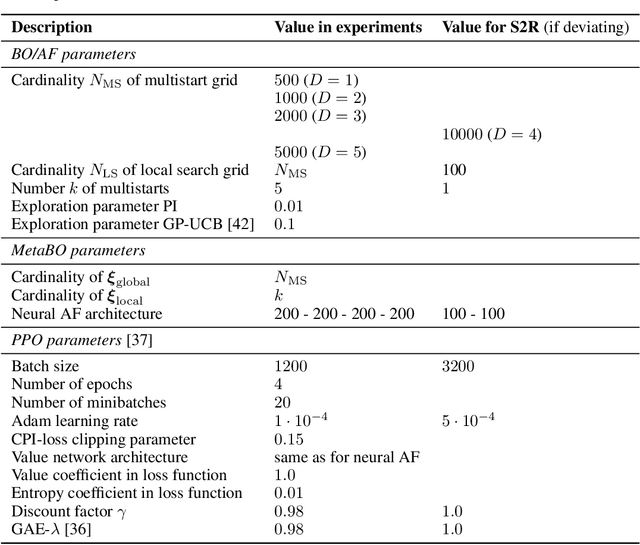
Many practical applications of machine learning require data-efficient black-box function optimization, e.g., to identify hyperparameters or process settings. However, readily available algorithms are typically designed to be universal optimizers and are, thus, often suboptimal for specific tasks. We therefore propose a method to learn optimizers which are automatically adapted to a given class of objective functions, e.g., in the context of sim-to-real applications. Instead of learning optimization from scratch, the proposed approach is firmly based within the famous Bayesian optimization framework. Only the acquisition function (AF) is replaced by a learned neural network and therefore the resulting algorithm is still able to exploit the proven generalization capabilities of Gaussian processes. We present experiments on several simulated as well as on a sim-to-real transfer task. The results show that the learned optimizers (1) consistently perform better than or on-par with known AFs on general function classes and (2) can automatically identify structural properties of a function class using cheap simulations and transfer this knowledge to adapt rapidly to real hardware tasks, thereby significantly outperforming existing problem-agnostic AFs.

Probabilistic Recurrent State-Space Models

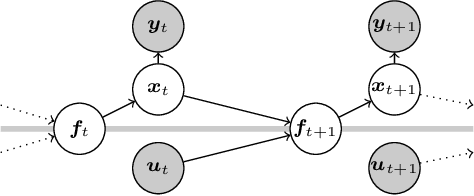
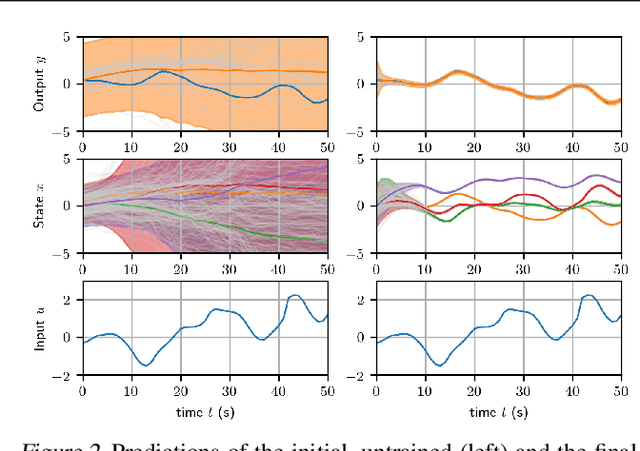
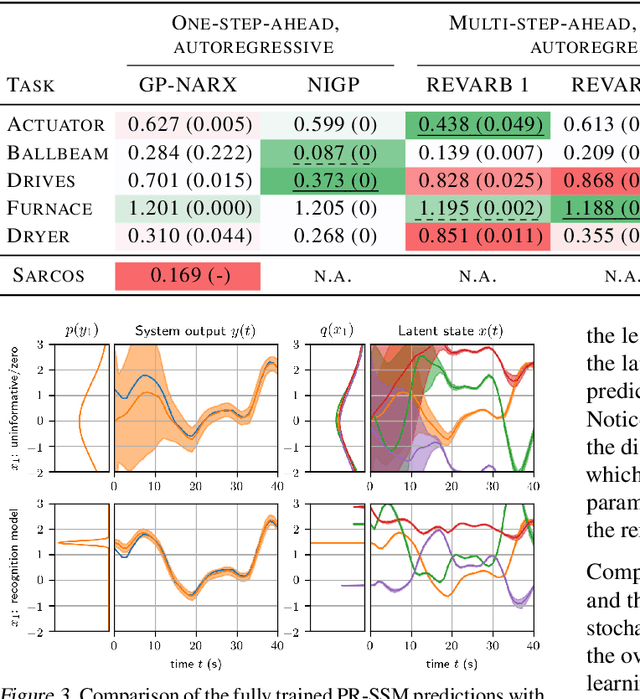
State-space models (SSMs) are a highly expressive model class for learning patterns in time series data and for system identification. Deterministic versions of SSMs (e.g. LSTMs) proved extremely successful in modeling complex time series data. Fully probabilistic SSMs, however, are often found hard to train, even for smaller problems. To overcome this limitation, we propose a novel model formulation and a scalable training algorithm based on doubly stochastic variational inference and Gaussian processes. In contrast to existing work, the proposed variational approximation allows one to fully capture the latent state temporal correlations. These correlations are the key to robust training. The effectiveness of the proposed PR-SSM is evaluated on a set of real-world benchmark datasets in comparison to state-of-the-art probabilistic model learning methods. Scalability and robustness are demonstrated on a high dimensional problem.