Uncertainty Representations in State-Space Layers for Deep Reinforcement Learning under Partial Observability

Optimal decision-making under partial observability requires reasoning about the uncertainty of the environment's hidden state. However, most reinforcement learning architectures handle partial observability with sequence models that have no internal mechanism to incorporate uncertainty in their hidden state representation, such as recurrent neural networks, deterministic state-space models and transformers. Inspired by advances in probabilistic world models for reinforcement learning, we propose a standalone Kalman filter layer that performs closed-form Gaussian inference in linear state-space models and train it end-to-end within a model-free architecture to maximize returns. Similar to efficient linear recurrent layers, the Kalman filter layer processes sequential data using a parallel scan, which scales logarithmically with the sequence length. By design, Kalman filter layers are a drop-in replacement for other recurrent layers in standard model-free architectures, but importantly they include an explicit mechanism for probabilistic filtering of the latent state representation. Experiments in a wide variety of tasks with partial observability show that Kalman filter layers excel in problems where uncertainty reasoning is key for decision-making, outperforming other stateful models.

Information-Theoretic Safe Bayesian Optimization

We consider a sequential decision making task, where the goal is to optimize an unknown function without evaluating parameters that violate an a~priori unknown (safety) constraint. A common approach is to place a Gaussian process prior on the unknown functions and allow evaluations only in regions that are safe with high probability. Most current methods rely on a discretization of the domain and cannot be directly extended to the continuous case. Moreover, the way in which they exploit regularity assumptions about the constraint introduces an additional critical hyperparameter. In this paper, we propose an information-theoretic safe exploration criterion that directly exploits the GP posterior to identify the most informative safe parameters to evaluate. The combination of this exploration criterion with a well known Bayesian optimization acquisition function yields a novel safe Bayesian optimization selection criterion. Our approach is naturally applicable to continuous domains and does not require additional explicit hyperparameters. We theoretically analyze the method and show that we do not violate the safety constraint with high probability and that we learn about the value of the safe optimum up to arbitrary precision. Empirical evaluations demonstrate improved data-efficiency and scalability.

Model-Based Epistemic Variance of Values for Risk-Aware Policy Optimization

We consider the problem of quantifying uncertainty over expected cumulative rewards in model-based reinforcement learning. In particular, we focus on characterizing the variance over values induced by a distribution over MDPs. Previous work upper bounds the posterior variance over values by solving a so-called uncertainty Bellman equation (UBE), but the over-approximation may result in inefficient exploration. We propose a new UBE whose solution converges to the true posterior variance over values and leads to lower regret in tabular exploration problems. We identify challenges to apply the UBE theory beyond tabular problems and propose a suitable approximation. Based on this approximation, we introduce a general-purpose policy optimization algorithm, Q-Uncertainty Soft Actor-Critic (QU-SAC), that can be applied for either risk-seeking or risk-averse policy optimization with minimal changes. Experiments in both online and offline RL demonstrate improved performance compared to other uncertainty estimation methods.

Scalable Meta-Learning with Gaussian Processes

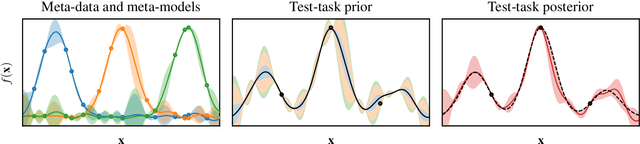
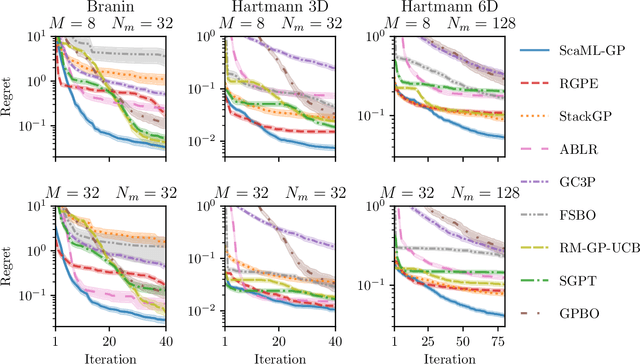
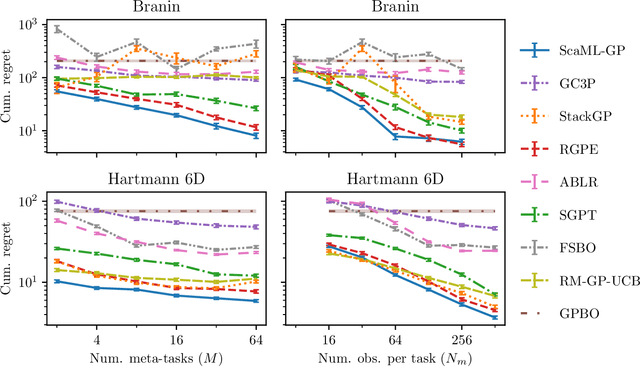
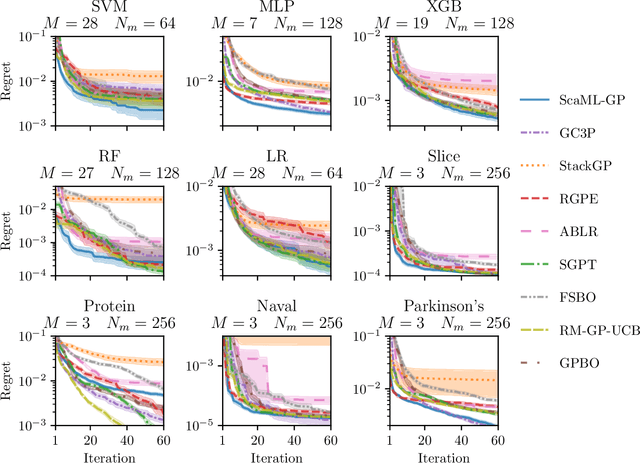
Meta-learning is a powerful approach that exploits historical data to quickly solve new tasks from the same distribution. In the low-data regime, methods based on the closed-form posterior of Gaussian processes (GP) together with Bayesian optimization have achieved high performance. However, these methods are either computationally expensive or introduce assumptions that hinder a principled propagation of uncertainty between task models. This may disrupt the balance between exploration and exploitation during optimization. In this paper, we develop ScaML-GP, a modular GP model for meta-learning that is scalable in the number of tasks. Our core contribution is a carefully designed multi-task kernel that enables hierarchical training and task scalability. Conditioning ScaML-GP on the meta-data exposes its modular nature yielding a test-task prior that combines the posteriors of meta-task GPs. In synthetic and real-world meta-learning experiments, we demonstrate that ScaML-GP can learn efficiently both with few and many meta-tasks.

Value-Distributional Model-Based Reinforcement Learning

Quantifying uncertainty about a policy's long-term performance is important to solve sequential decision-making tasks. We study the problem from a model-based Bayesian reinforcement learning perspective, where the goal is to learn the posterior distribution over value functions induced by parameter (epistemic) uncertainty of the Markov decision process. Previous work restricts the analysis to a few moments of the distribution over values or imposes a particular distribution shape, e.g., Gaussians. Inspired by distributional reinforcement learning, we introduce a Bellman operator whose fixed-point is the value distribution function. Based on our theory, we propose Epistemic Quantile-Regression (EQR), a model-based algorithm that learns a value distribution function that can be used for policy optimization. Evaluation across several continuous-control tasks shows performance benefits with respect to established model-based and model-free algorithms.

Model-Based Uncertainty in Value Functions

We consider the problem of quantifying uncertainty over expected cumulative rewards in model-based reinforcement learning. In particular, we focus on characterizing the variance over values induced by a distribution over MDPs. Previous work upper bounds the posterior variance over values by solving a so-called uncertainty Bellman equation, but the over-approximation may result in inefficient exploration. We propose a new uncertainty Bellman equation whose solution converges to the true posterior variance over values and explicitly characterizes the gap in previous work. Moreover, our uncertainty quantification technique is easily integrated into common exploration strategies and scales naturally beyond the tabular setting by using standard deep reinforcement learning architectures. Experiments in difficult exploration tasks, both in tabular and continuous control settings, show that our sharper uncertainty estimates improve sample-efficiency.

Information-Theoretic Safe Exploration with Gaussian Processes

We consider a sequential decision making task where we are not allowed to evaluate parameters that violate an a priori unknown (safety) constraint. A common approach is to place a Gaussian process prior on the unknown constraint and allow evaluations only in regions that are safe with high probability. Most current methods rely on a discretization of the domain and cannot be directly extended to the continuous case. Moreover, the way in which they exploit regularity assumptions about the constraint introduces an additional critical hyperparameter. In this paper, we propose an information-theoretic safe exploration criterion that directly exploits the GP posterior to identify the most informative safe parameters to evaluate. Our approach is naturally applicable to continuous domains and does not require additional hyperparameters. We theoretically analyze the method and show that we do not violate the safety constraint with high probability and that we explore by learning about the constraint up to arbitrary precision. Empirical evaluations demonstrate improved data-efficiency and scalability.

Transfer Learning with Gaussian Processes for Bayesian Optimization

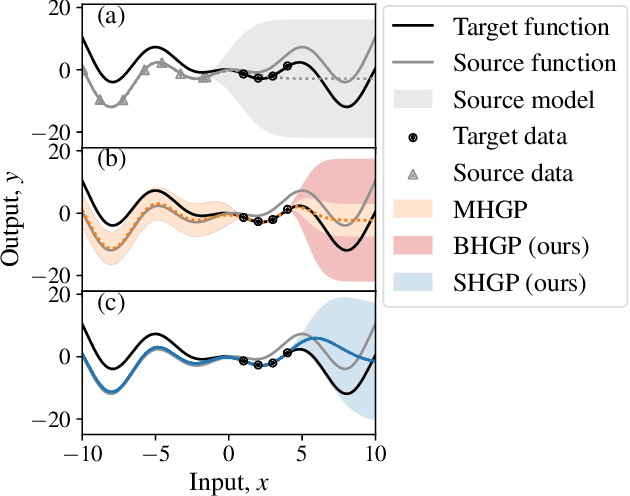
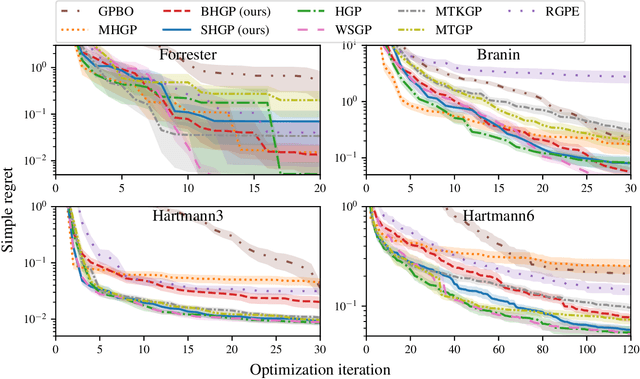
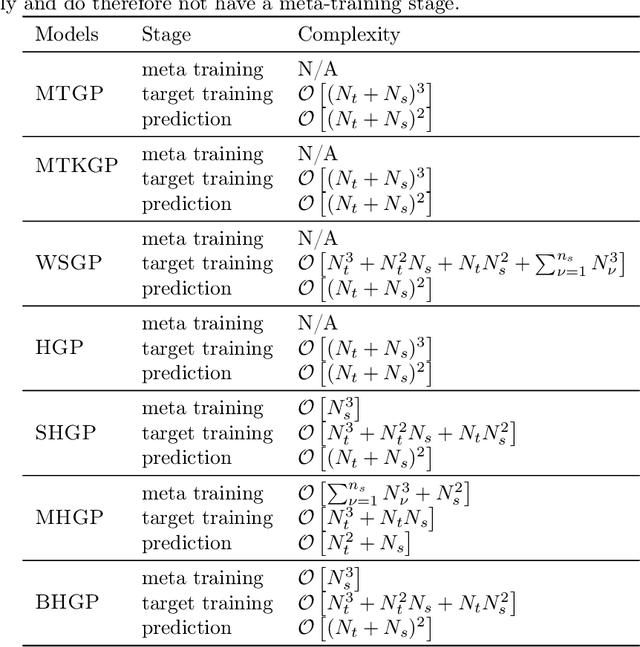
Bayesian optimization is a powerful paradigm to optimize black-box functions based on scarce and noisy data. Its data efficiency can be further improved by transfer learning from related tasks. While recent transfer models meta-learn a prior based on large amount of data, in the low-data regime methods that exploit the closed-form posterior of Gaussian processes (GPs) have an advantage. In this setting, several analytically tractable transfer-model posteriors have been proposed, but the relative advantages of these methods are not well understood. In this paper, we provide a unified view on hierarchical GP models for transfer learning, which allows us to analyze the relationship between methods. As part of the analysis, we develop a novel closed-form boosted GP transfer model that fits between existing approaches in terms of complexity. We evaluate the performance of the different approaches in large-scale experiments and highlight strengths and weaknesses of the different transfer-learning methods.

Noisy-Input Entropy Search for Efficient Robust Bayesian Optimization

We consider the problem of robust optimization within the well-established Bayesian optimization (BO) framework. While BO is intrinsically robust to noisy evaluations of the objective function, standard approaches do not consider the case of uncertainty about the input parameters. In this paper, we propose Noisy-Input Entropy Search (NES), a novel information-theoretic acquisition function that is designed to find robust optima for problems with both input and measurement noise. NES is based on the key insight that the robust objective in many cases can be modeled as a Gaussian process, however, it cannot be observed directly. We evaluate NES on several benchmark problems from the optimization literature and from engineering. The results show that NES reliably finds robust optima, outperforming existing methods from the literature on all benchmarks.