On-Policy Model Errors in Reinforcement Learning

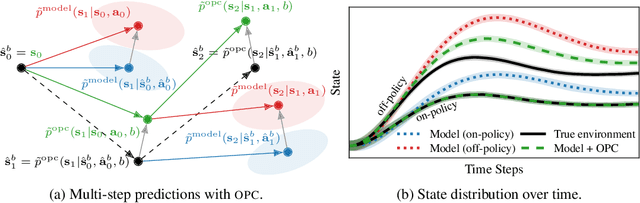
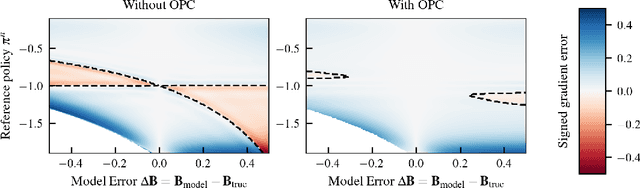
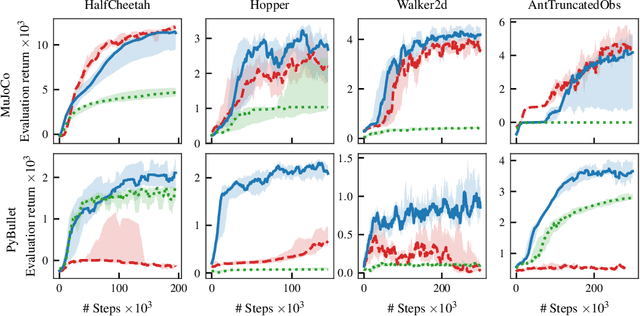
Model-free reinforcement learning algorithms can compute policy gradients given sampled environment transitions, but require large amounts of data. In contrast, model-based methods can use the learned model to generate new data, but model errors and bias can render learning unstable or sub-optimal. In this paper, we present a novel method that combines real world data and a learned model in order to get the best of both worlds. The core idea is to exploit the real world data for on-policy predictions and use the learned model only to generalize to different actions. Specifically, we use the data as time-dependent on-policy correction terms on top of a learned model, to retain the ability to generate data without accumulating errors over long prediction horizons. We motivate this method theoretically and show that it counteracts an error term for model-based policy improvement. Experiments on MuJoCo- and PyBullet-benchmarks show that our method can drastically improve existing model-based approaches without introducing additional tuning parameters.

Model Learning and Contextual Controller Tuning for Autonomous Racing

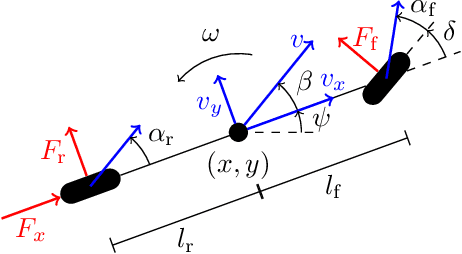
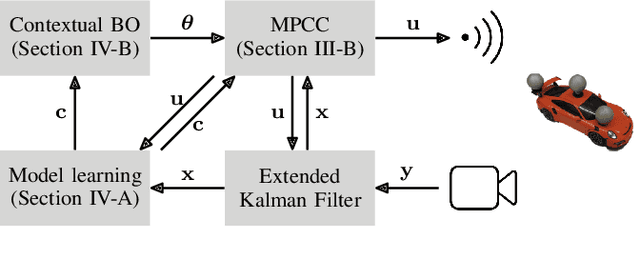
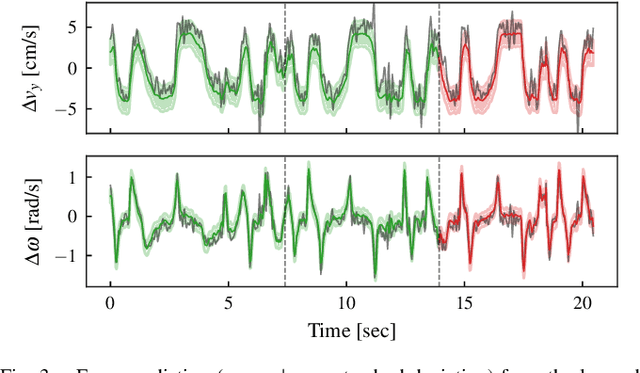
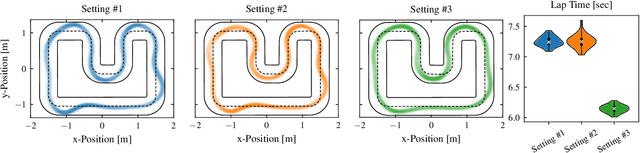
Model predictive control has been widely used in the field of autonomous racing and many data-driven approaches have been proposed to improve the closed-loop performance and to minimize lap time. However, it is often overlooked that a change in the environmental conditions, e.g., when it starts raining, it is not only required to adapt the predictive model but also the controller parameters need to be adjusted. In this paper, we address this challenge with the goal of requiring only few data. The key novelty of the proposed approach is that we leverage the learned dynamics model to encode the environmental condition as context. This insight allows us to employ contextual Bayesian optimization, thus accelerating the controller tuning problem when the environment changes and to transfer knowledge across different cars. The proposed framework is validated on an experimental platform with 1:28 scale RC race cars. We perform an extensive evaluation with more than 2'000 driven laps demonstrating that our approach successfully optimizes the lap time across different contexts faster compared to standard Bayesian optimization.

Cautious Bayesian Optimization for Efficient and Scalable Policy Search

Sample efficiency is one of the key factors when applying policy search to real-world problems. In recent years, Bayesian Optimization (BO) has become prominent in the field of robotics due to its sample efficiency and little prior knowledge needed. However, one drawback of BO is its poor performance on high-dimensional search spaces as it focuses on global search. In the policy search setting, local optimization is typically sufficient as initial policies are often available, e.g., via meta-learning, kinesthetic demonstrations or sim-to-real approaches. In this paper, we propose to constrain the policy search space to a sublevel-set of the Bayesian surrogate model's predictive uncertainty. This simple yet effective way of constraining the policy update enables BO to scale to high-dimensional spaces (>100) as well as reduces the risk of damaging the system. We demonstrate the effectiveness of our approach on a wide range of problems, including a motor skills task, adapting deep RL agents to new reward signals and a sim-to-real task for an inverted pendulum system.

Noisy-Input Entropy Search for Efficient Robust Bayesian Optimization

We consider the problem of robust optimization within the well-established Bayesian optimization (BO) framework. While BO is intrinsically robust to noisy evaluations of the objective function, standard approaches do not consider the case of uncertainty about the input parameters. In this paper, we propose Noisy-Input Entropy Search (NES), a novel information-theoretic acquisition function that is designed to find robust optima for problems with both input and measurement noise. NES is based on the key insight that the robust objective in many cases can be modeled as a Gaussian process, however, it cannot be observed directly. We evaluate NES on several benchmark problems from the optimization literature and from engineering. The results show that NES reliably finds robust optima, outperforming existing methods from the literature on all benchmarks.

Bayesian Optimization for Policy Search in High-Dimensional Systems via Automatic Domain Selection

Bayesian Optimization (BO) is an effective method for optimizing expensive-to-evaluate black-box functions with a wide range of applications for example in robotics, system design and parameter optimization. However, scaling BO to problems with large input dimensions (>10) remains an open challenge. In this paper, we propose to leverage results from optimal control to scale BO to higher dimensional control tasks and to reduce the need for manually selecting the optimization domain. The contributions of this paper are twofold: 1) We show how we can make use of a learned dynamics model in combination with a model-based controller to simplify the BO problem by focusing onto the most relevant regions of the optimization domain. 2) Based on (1) we present a method to find an embedding in parameter space that reduces the effective dimensionality of the optimization problem. To evaluate the effectiveness of the proposed approach, we present an experimental evaluation on real hardware, as well as simulated tasks including a 48-dimensional policy for a quadcopter.

On Simulation and Trajectory Prediction with Gaussian Process Dynamics

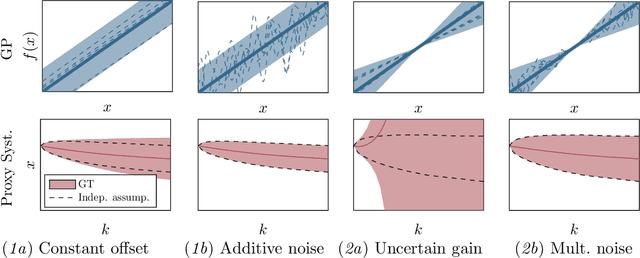
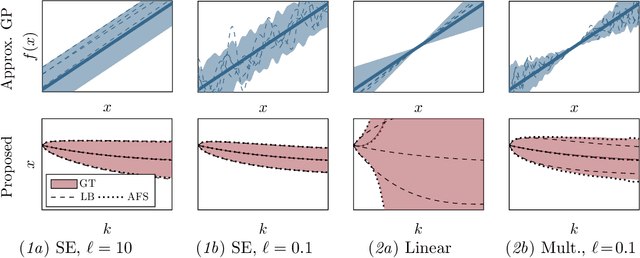
Established techniques for simulation and prediction with Gaussian process (GP) dynamics often implicitly make use of an independence assumption on successive function evaluations of the dynamics model. This can result in significant error and underestimation of the prediction uncertainty, potentially leading to failures in safety-critical applications. This paper discusses methods that explicitly take the correlation of successive function evaluations into account. We first describe two sampling-based techniques; one approach provides samples of the true trajectory distribution, suitable for `ground truth' simulations, while the other draws function samples from basis function approximations of the GP. Second, we propose a linearization-based technique that directly provides approximations of the trajectory distribution, taking correlations explicitly into account. We demonstrate the procedures in simple numerical examples, contrasting the results with established methods.