Bayesian Multi-Task Learning MPC for Robotic Mobile Manipulation

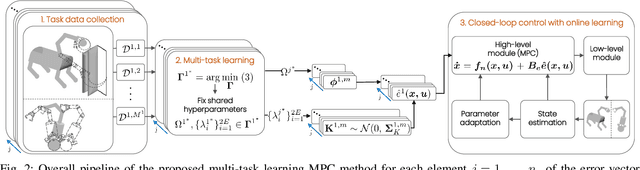
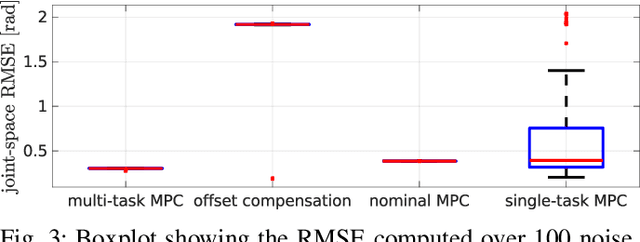
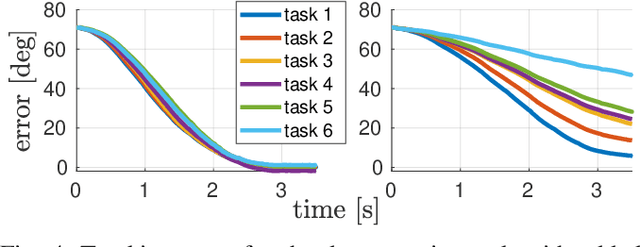
Mobile manipulation in robotics is challenging due to the need of solving many diverse tasks, such as opening a door or picking-and-placing an object. Typically, a basic first-principles system description of the robot is available, thus motivating the use of model-based controllers. However, the robot dynamics and its interaction with an object are affected by uncertainty, limiting the controller's performance. To tackle this problem, we propose a Bayesian multi-task learning model that uses trigonometric basis functions to identify the error in the dynamics. In this way, data from different but related tasks can be leveraged to provide a descriptive error model that can be efficiently updated online for new, unseen tasks. We combine this learning scheme with a model predictive controller, and extensively test the effectiveness of the proposed approach, including comparisons with available baseline controllers. We present simulation tests with a ball-balancing robot, and door-opening hardware experiments with a quadrupedal manipulator.

Model Learning and Contextual Controller Tuning for Autonomous Racing

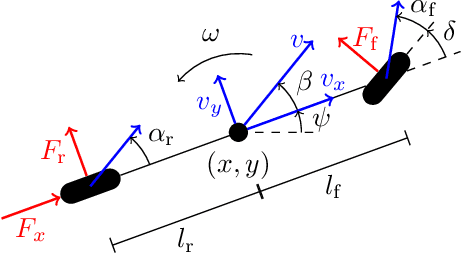
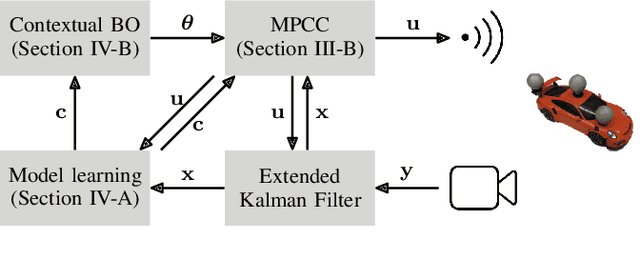
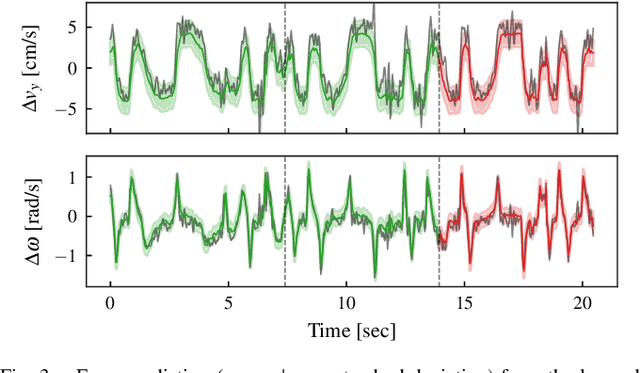
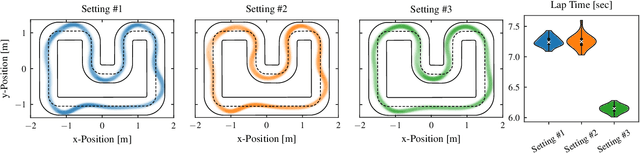
Model predictive control has been widely used in the field of autonomous racing and many data-driven approaches have been proposed to improve the closed-loop performance and to minimize lap time. However, it is often overlooked that a change in the environmental conditions, e.g., when it starts raining, it is not only required to adapt the predictive model but also the controller parameters need to be adjusted. In this paper, we address this challenge with the goal of requiring only few data. The key novelty of the proposed approach is that we leverage the learned dynamics model to encode the environmental condition as context. This insight allows us to employ contextual Bayesian optimization, thus accelerating the controller tuning problem when the environment changes and to transfer knowledge across different cars. The proposed framework is validated on an experimental platform with 1:28 scale RC race cars. We perform an extensive evaluation with more than 2'000 driven laps demonstrating that our approach successfully optimizes the lap time across different contexts faster compared to standard Bayesian optimization.

Meta Learning MPC using Finite-Dimensional Gaussian Process Approximations

Data availability has dramatically increased in recent years, driving model-based control methods to exploit learning techniques for improving the system description, and thus control performance. Two key factors that hinder the practical applicability of learning methods in control are their high computational complexity and limited generalization capabilities to unseen conditions. Meta-learning is a powerful tool that enables efficient learning across a finite set of related tasks, easing adaptation to new unseen tasks. This paper makes use of a meta-learning approach for adaptive model predictive control, by learning a system model that leverages data from previous related tasks, while enabling fast fine-tuning to the current task during closed-loop operation. The dynamics is modeled via Gaussian process regression and, building on the Karhunen-Lo{\`e}ve expansion, can be approximately reformulated as a finite linear combination of kernel eigenfunctions. Using data collected over a set of tasks, the eigenfunction hyperparameters are optimized in a meta-training phase by maximizing a variational bound for the log-marginal likelihood. During meta-testing, the eigenfunctions are fixed, so that only the linear parameters are adapted to the new unseen task in an online adaptive fashion via Bayesian linear regression, providing a simple and efficient inference scheme. Simulation results are provided for autonomous racing with miniature race cars adapting to unseen road conditions.

On Simulation and Trajectory Prediction with Gaussian Process Dynamics

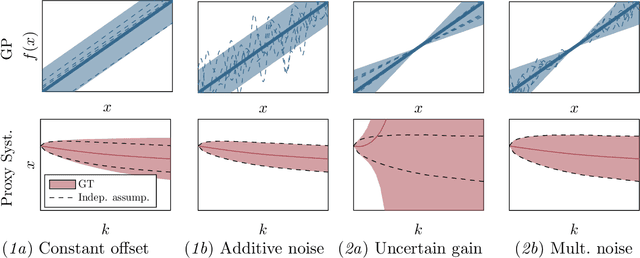
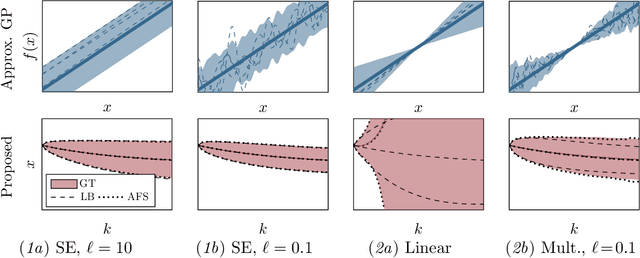
Established techniques for simulation and prediction with Gaussian process (GP) dynamics often implicitly make use of an independence assumption on successive function evaluations of the dynamics model. This can result in significant error and underestimation of the prediction uncertainty, potentially leading to failures in safety-critical applications. This paper discusses methods that explicitly take the correlation of successive function evaluations into account. We first describe two sampling-based techniques; one approach provides samples of the true trajectory distribution, suitable for `ground truth' simulations, while the other draws function samples from basis function approximations of the GP. Second, we propose a linearization-based technique that directly provides approximations of the trajectory distribution, taking correlations explicitly into account. We demonstrate the procedures in simple numerical examples, contrasting the results with established methods.