On Simulation and Trajectory Prediction with Gaussian Process Dynamics
Paper and Code
Dec 24, 2019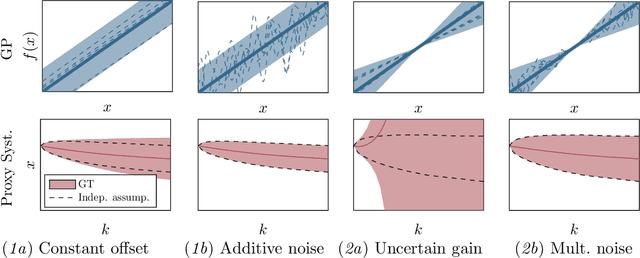
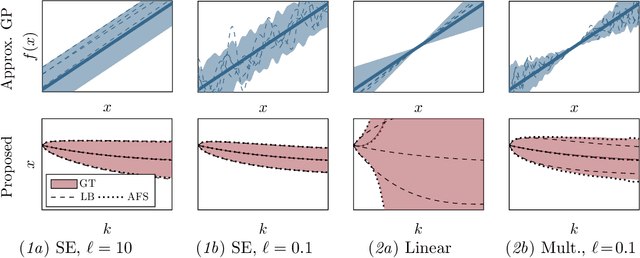
Established techniques for simulation and prediction with Gaussian process (GP) dynamics often implicitly make use of an independence assumption on successive function evaluations of the dynamics model. This can result in significant error and underestimation of the prediction uncertainty, potentially leading to failures in safety-critical applications. This paper discusses methods that explicitly take the correlation of successive function evaluations into account. We first describe two sampling-based techniques; one approach provides samples of the true trajectory distribution, suitable for `ground truth' simulations, while the other draws function samples from basis function approximations of the GP. Second, we propose a linearization-based technique that directly provides approximations of the trajectory distribution, taking correlations explicitly into account. We demonstrate the procedures in simple numerical examples, contrasting the results with established methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge