SMOG: Scalable Meta-Learning for Multi-Objective Bayesian Optimization

Multi-objective optimization aims to solve problems with competing objectives, often with only black-box access to a problem and a limited budget of measurements. In many applications, historical data from related optimization tasks is available, creating an opportunity for meta-learning to accelerate the optimization. Bayesian optimization, as a promising technique for black-box optimization, has been extended to meta-learning and multi-objective optimization independently, but methods that simultaneously address both settings - meta-learned priors for multi-objective Bayesian optimization - remain largely unexplored. We propose SMOG, a scalable and modular meta-learning model based on a multi-output Gaussian process that explicitly learns correlations between objectives. SMOG builds a structured joint Gaussian process prior across meta- and target tasks and, after conditioning on metadata, yields a closed-form target-task prior augmented by a flexible residual multi-output kernel. This construction propagates metadata uncertainty into the target surrogate in a principled way. SMOG supports hierarchical, parallel training: meta-task Gaussian processes are fit once and then cached, achieving linear scaling with the number of meta-tasks. The resulting surrogate integrates seamlessly with standard multi-objective Bayesian optimization acquisition functions.

Scalable Meta-Learning with Gaussian Processes

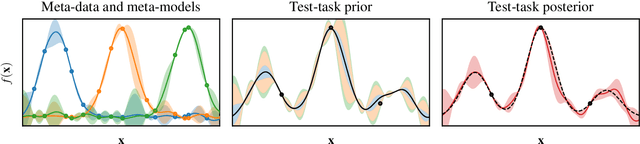
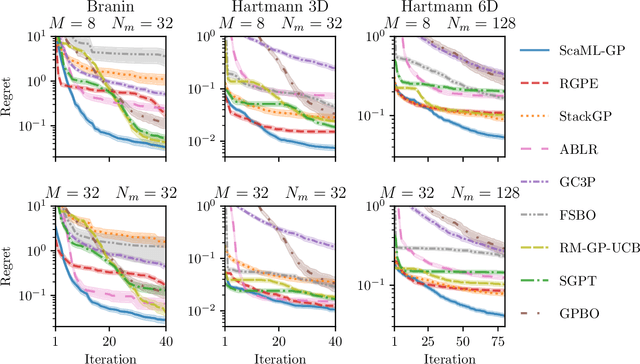
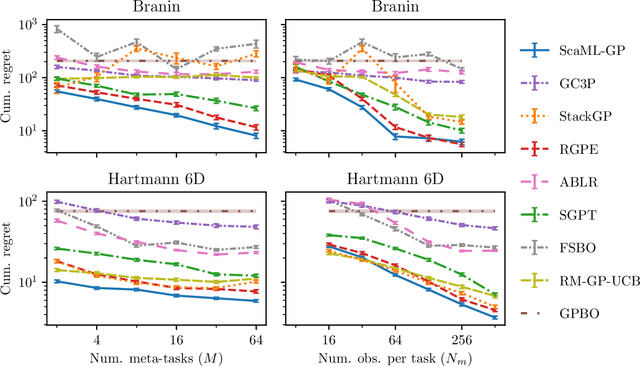
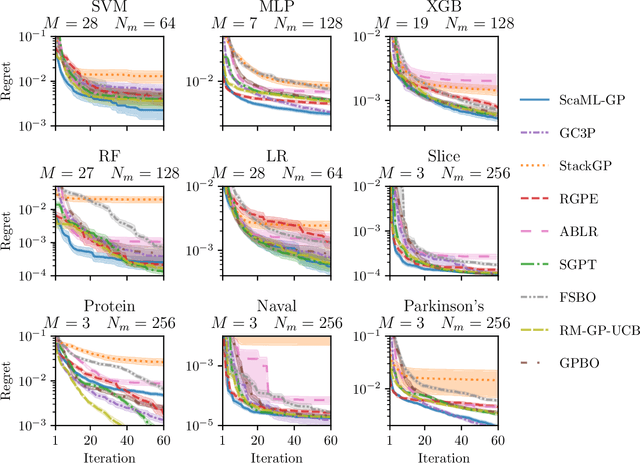
Meta-learning is a powerful approach that exploits historical data to quickly solve new tasks from the same distribution. In the low-data regime, methods based on the closed-form posterior of Gaussian processes (GP) together with Bayesian optimization have achieved high performance. However, these methods are either computationally expensive or introduce assumptions that hinder a principled propagation of uncertainty between task models. This may disrupt the balance between exploration and exploitation during optimization. In this paper, we develop ScaML-GP, a modular GP model for meta-learning that is scalable in the number of tasks. Our core contribution is a carefully designed multi-task kernel that enables hierarchical training and task scalability. Conditioning ScaML-GP on the meta-data exposes its modular nature yielding a test-task prior that combines the posteriors of meta-task GPs. In synthetic and real-world meta-learning experiments, we demonstrate that ScaML-GP can learn efficiently both with few and many meta-tasks.

Transfer Learning with Gaussian Processes for Bayesian Optimization

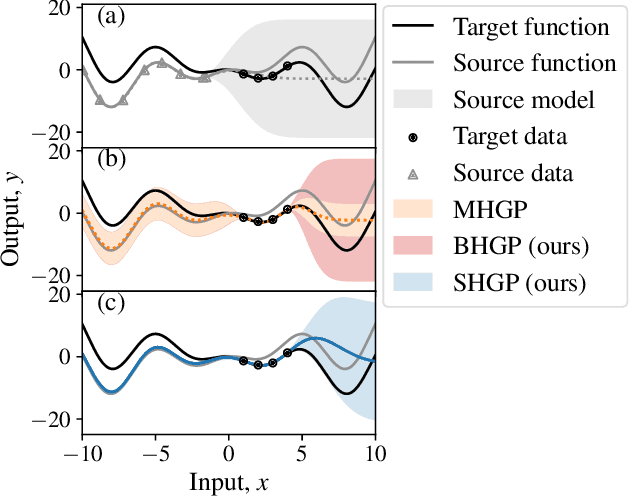
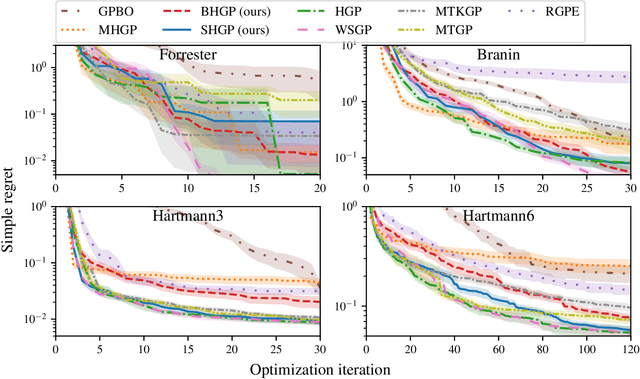
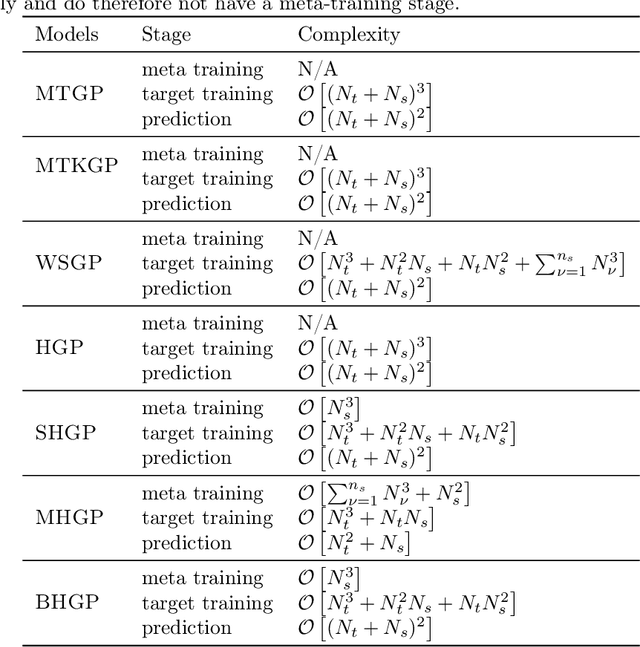
Bayesian optimization is a powerful paradigm to optimize black-box functions based on scarce and noisy data. Its data efficiency can be further improved by transfer learning from related tasks. While recent transfer models meta-learn a prior based on large amount of data, in the low-data regime methods that exploit the closed-form posterior of Gaussian processes (GPs) have an advantage. In this setting, several analytically tractable transfer-model posteriors have been proposed, but the relative advantages of these methods are not well understood. In this paper, we provide a unified view on hierarchical GP models for transfer learning, which allows us to analyze the relationship between methods. As part of the analysis, we develop a novel closed-form boosted GP transfer model that fits between existing approaches in terms of complexity. We evaluate the performance of the different approaches in large-scale experiments and highlight strengths and weaknesses of the different transfer-learning methods.