LSP : Acceleration and Regularization of Graph Neural Networks via Locality Sensitive Pruning of Graphs

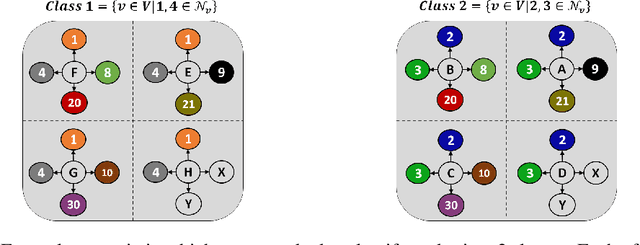
Graph Neural Networks (GNNs) have emerged as highly successful tools for graph-related tasks. However, real-world problems involve very large graphs, and the compute resources needed to fit GNNs to those problems grow rapidly. Moreover, the noisy nature and size of real-world graphs cause GNNs to over-fit if not regularized properly. Surprisingly, recent works show that large graphs often involve many redundant components that can be removed without compromising the performance too much. This includes node or edge removals during inference through GNNs layers or as a pre-processing step that sparsifies the input graph. This intriguing phenomenon enables the development of state-of-the-art GNNs that are both efficient and accurate. In this paper, we take a further step towards demystifying this phenomenon and propose a systematic method called Locality-Sensitive Pruning (LSP) for graph pruning based on Locality-Sensitive Hashing. We aim to sparsify a graph so that similar local environments of the original graph result in similar environments in the resulting sparsified graph, which is an essential feature for graph-related tasks. To justify the application of pruning based on local graph properties, we exemplify the advantage of applying pruning based on locality properties over other pruning strategies in various scenarios. Extensive experiments on synthetic and real-world datasets demonstrate the superiority of LSP, which removes a significant amount of edges from large graphs without compromising the performance, accompanied by a considerable acceleration.

SOLO: Search Online, Learn Offline for Combinatorial Optimization Problems

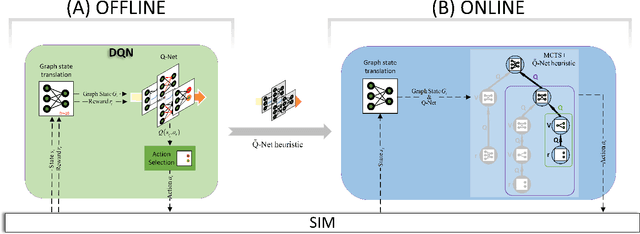
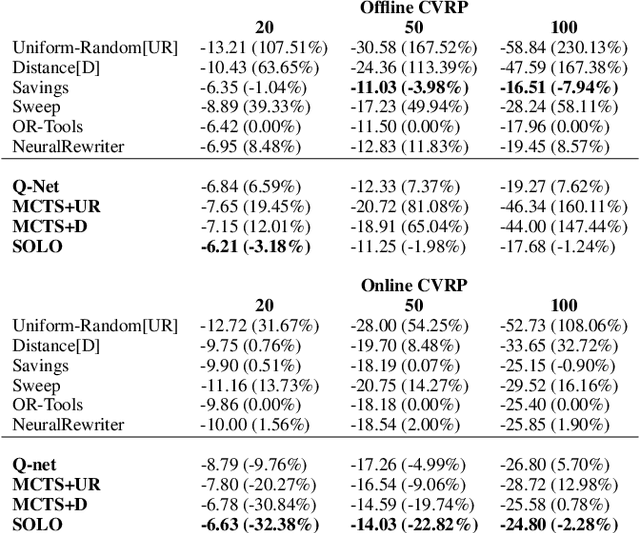
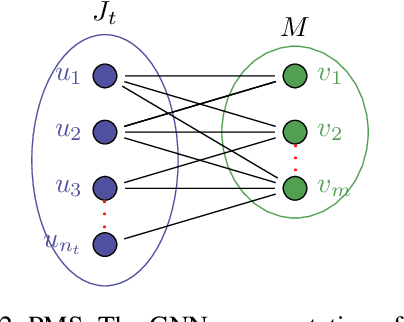
We study combinatorial problems with real world applications such as machine scheduling, routing, and assignment. We propose a method that combines Reinforcement Learning (RL) and planning. This method can equally be applied to both the offline, as well as online, variants of the combinatorial problem, in which the problem components (e.g., jobs in scheduling problems) are not known in advance, but rather arrive during the decision-making process. Our solution is quite generic, scalable, and leverages distributional knowledge of the problem parameters. We frame the solution process as an MDP, and take a Deep Q-Learning approach wherein states are represented as graphs, thereby allowing our trained policies to deal with arbitrary changes in a principled manner. Though learned policies work well in expectation, small deviations can have substantial negative effects in combinatorial settings. We mitigate these drawbacks by employing our graph-convolutional policies as non-optimal heuristics in a compatible search algorithm, Monte Carlo Tree Search, to significantly improve overall performance. We demonstrate our method on two problems: Machine Scheduling and Capacitated Vehicle Routing. We show that our method outperforms custom-tailored mathematical solvers, state of the art learning-based algorithms, and common heuristics, both in computation time and performance.

Practical Risk Measures in Reinforcement Learning

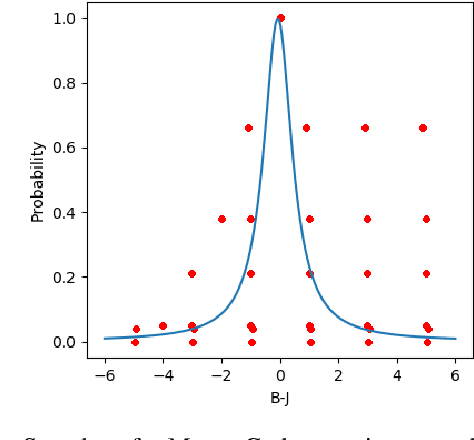
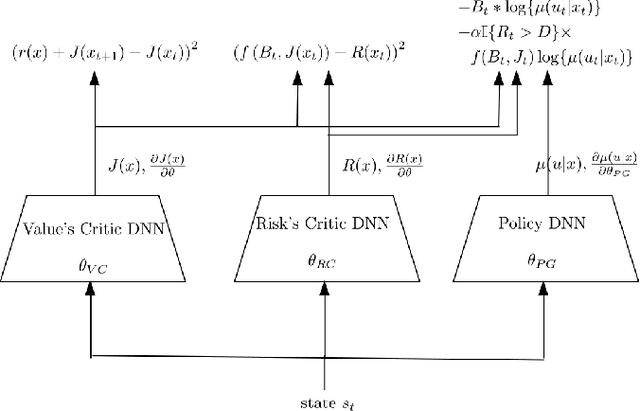
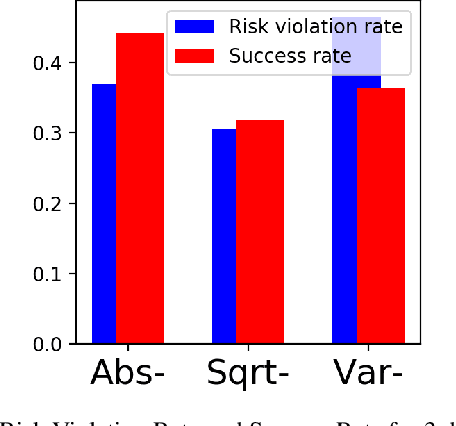
Practical application of Reinforcement Learning (RL) often involves risk considerations. We study a generalized approximation scheme for risk measures, based on Monte-Carlo simulations, where the risk measures need not necessarily be \emph{coherent}. We demonstrate that, even in simple problems, measures such as the variance of the reward-to-go do not capture the risk in a satisfactory manner. In addition, we show how a risk measure can be derived from model's realizations. We propose a neural architecture for estimating the risk and suggest the risk critic architecture that can be use to optimize a policy under general risk measures. We conclude our work with experiments that demonstrate the efficacy of our approach.