Latent Task-Specific Graph Network Simulators

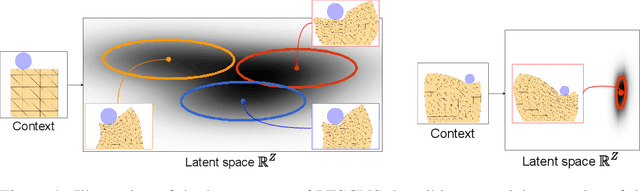
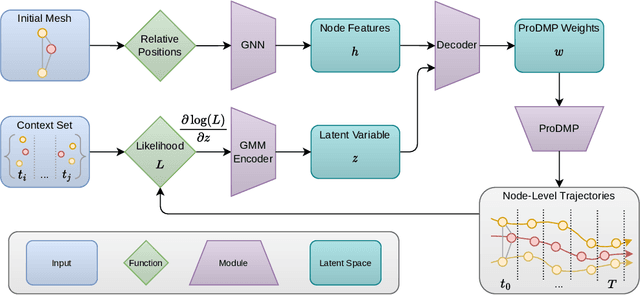
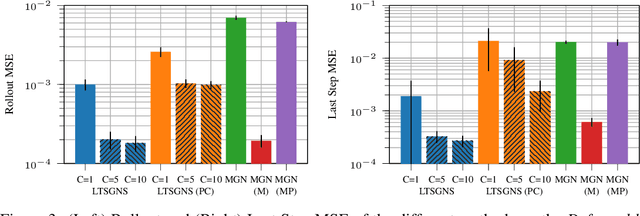
Simulating dynamic physical interactions is a critical challenge across multiple scientific domains, with applications ranging from robotics to material science. For mesh-based simulations, Graph Network Simulators (GNSs) pose an efficient alternative to traditional physics-based simulators. Their inherent differentiability and speed make them particularly well-suited for inverse design problems. Yet, adapting to new tasks from limited available data is an important aspect for real-world applications that current methods struggle with. We frame mesh-based simulation as a meta-learning problem and use a recent Bayesian meta-learning method to improve GNSs adaptability to new scenarios by leveraging context data and handling uncertainties. Our approach, latent task-specific graph network simulator, uses non-amortized task posterior approximations to sample latent descriptions of unknown system properties. Additionally, we leverage movement primitives for efficient full trajectory prediction, effectively addressing the issue of accumulating errors encountered by previous auto-regressive methods. We validate the effectiveness of our approach through various experiments, performing on par with or better than established baseline methods. Movement primitives further allow us to accommodate various types of context data, as demonstrated through the utilization of point clouds during inference. By combining GNSs with meta-learning, we bring them closer to real-world applicability, particularly in scenarios with smaller datasets.

Beyond Deep Ensembles: A Large-Scale Evaluation of Bayesian Deep Learning under Distribution Shift

Bayesian deep learning (BDL) is a promising approach to achieve well-calibrated predictions on distribution-shifted data. Nevertheless, there exists no large-scale survey that evaluates recent SOTA methods on diverse, realistic, and challenging benchmark tasks in a systematic manner. To provide a clear picture of the current state of BDL research, we evaluate modern BDL algorithms on real-world datasets from the WILDS collection containing challenging classification and regression tasks, with a focus on generalization capability and calibration under distribution shift. We compare the algorithms on a wide range of large, convolutional and transformer-based neural network architectures. In particular, we investigate a signed version of the expected calibration error that reveals whether the methods are over- or under-confident, providing further insight into the behavior of the methods. Further, we provide the first systematic evaluation of BDL for fine-tuning large pre-trained models, where training from scratch is prohibitively expensive. Finally, given the recent success of Deep Ensembles, we extend popular single-mode posterior approximations to multiple modes by the use of ensembles. While we find that ensembling single-mode approximations generally improves the generalization capability and calibration of the models by a significant margin, we also identify a failure mode of ensembles when finetuning large transformer-based language models. In this setting, variational inference based approaches such as last-layer Bayes By Backprop outperform other methods in terms of accuracy by a large margin, while modern approximate inference algorithms such as SWAG achieve the best calibration.

Beyond Deep Ensembles -- A Large-Scale Evaluation of Bayesian Deep Learning under Distribution Shift

Bayesian deep learning (BDL) is a promising approach to achieve well-calibrated predictions on distribution-shifted data. Nevertheless, there exists no large-scale survey that evaluates recent SOTA methods on diverse, realistic, and challenging benchmark tasks in a systematic manner. To provide a clear picture of the current state of BDL research, we evaluate modern BDL algorithms on real-world datasets from the WILDS collection containing challenging classification and regression tasks, with a focus on generalization capability and calibration under distribution shift. We compare the algorithms on a wide range of large, convolutional and transformer-based neural network architectures. In particular, we investigate a signed version of the expected calibration error that reveals whether the methods are over- or under-confident, providing further insight into the behavior of the methods. Further, we provide the first systematic evaluation of BDL for fine-tuning large pre-trained models, where training from scratch is prohibitively expensive. Finally, given the recent success of Deep Ensembles, we extend popular single-mode posterior approximations to multiple modes by the use of ensembles. While we find that ensembling single-mode approximations generally improves the generalization capability and calibration of the models by a significant margin, we also identify a failure mode of ensembles when finetuning large transformer-based language models. In this setting, variational inference based approaches such as last-layer Bayes By Backprop outperform other methods in terms of accuracy by a large margin, while modern approximate inference algorithms such as SWAG achieve the best calibration.

ProDMPs: A Unified Perspective on Dynamic and Probabilistic Movement Primitives

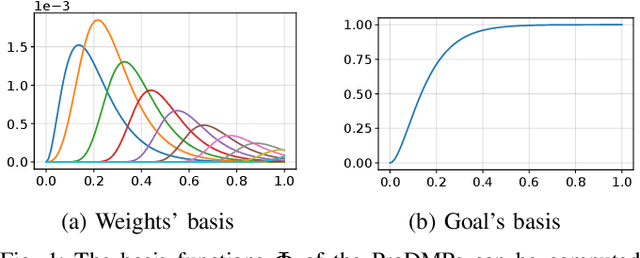
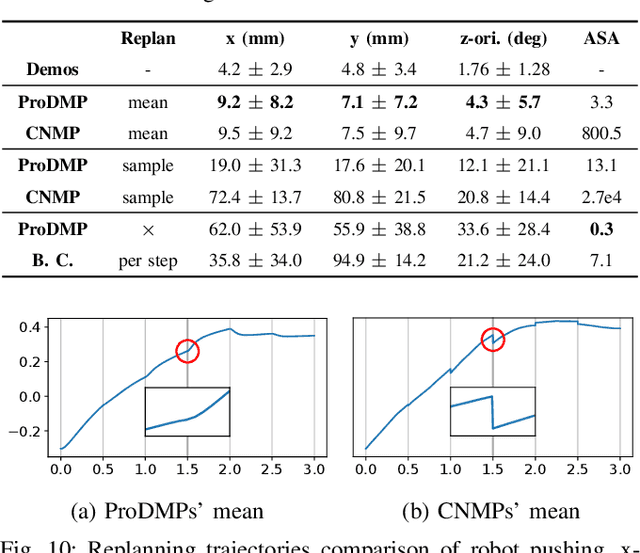
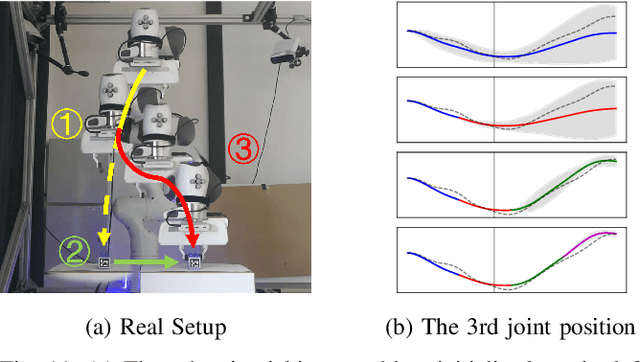
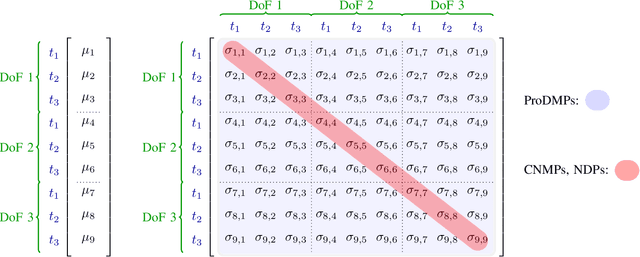
Movement Primitives (MPs) are a well-known concept to represent and generate modular trajectories. MPs can be broadly categorized into two types: (a) dynamics-based approaches that generate smooth trajectories from any initial state, e. g., Dynamic Movement Primitives (DMPs), and (b) probabilistic approaches that capture higher-order statistics of the motion, e. g., Probabilistic Movement Primitives (ProMPs). To date, however, there is no method that unifies both, i. e. that can generate smooth trajectories from an arbitrary initial state while capturing higher-order statistics. In this paper, we introduce a unified perspective of both approaches by solving the ODE underlying the DMPs. We convert expensive online numerical integration of DMPs into basis functions that can be computed offline. These basis functions can be used to represent trajectories or trajectory distributions similar to ProMPs while maintaining all the properties of dynamical systems. Since we inherit the properties of both methodologies, we call our proposed model Probabilistic Dynamic Movement Primitives (ProDMPs). Additionally, we embed ProDMPs in deep neural network architecture and propose a new cost function for efficient end-to-end learning of higher-order trajectory statistics. To this end, we leverage Bayesian Aggregation for non-linear iterative conditioning on sensory inputs. Our proposed model achieves smooth trajectory generation, goal-attractor convergence, correlation analysis, non-linear conditioning, and online re-planing in one framework.

A Unified Perspective on Natural Gradient Variational Inference with Gaussian Mixture Models

Variational inference with Gaussian mixture models (GMMs) enables learning of highly-tractable yet multi-modal approximations of intractable target distributions. GMMs are particular relevant for problem settings with up to a few hundred dimensions, for example in robotics, for modelling distributions over trajectories or joint distributions. This work focuses on two very effective methods for GMM-based variational inference that both employ independent natural gradient updates for the individual components and the categorical distribution of the weights. We show for the first time, that their derived updates are equivalent, although their practical implementations and theoretical guarantees differ. We identify several design choices that distinguish both approaches, namely with respect to sample selection, natural gradient estimation, stepsize adaptation, and whether trust regions are enforced or the number of components adapted. We perform extensive ablations on these design choices and show that they strongly affect the efficiency of the optimization and the variability of the learned distribution. Based on our insights, we propose a novel instantiation of our generalized framework, that combines first-order natural gradient estimates with trust-regions and component adaption, and significantly outperforms both previous methods in all our experiments.

What Matters For Meta-Learning Vision Regression Tasks?

Meta-learning is widely used in few-shot classification and function regression due to its ability to quickly adapt to unseen tasks. However, it has not yet been well explored on regression tasks with high dimensional inputs such as images. This paper makes two main contributions that help understand this barely explored area. \emph{First}, we design two new types of cross-category level vision regression tasks, namely object discovery and pose estimation of unprecedented complexity in the meta-learning domain for computer vision. To this end, we (i) exhaustively evaluate common meta-learning techniques on these tasks, and (ii) quantitatively analyze the effect of various deep learning techniques commonly used in recent meta-learning algorithms in order to strengthen the generalization capability: data augmentation, domain randomization, task augmentation and meta-regularization. Finally, we (iii) provide some insights and practical recommendations for training meta-learning algorithms on vision regression tasks. \emph{Second}, we propose the addition of functional contrastive learning (FCL) over the task representations in Conditional Neural Processes (CNPs) and train in an end-to-end fashion. The experimental results show that the results of prior work are misleading as a consequence of a poor choice of the loss function as well as too small meta-training sets. Specifically, we find that CNPs outperform MAML on most tasks without fine-tuning. Furthermore, we observe that naive task augmentation without a tailored design results in underfitting.

Trajectory-Based Off-Policy Deep Reinforcement Learning

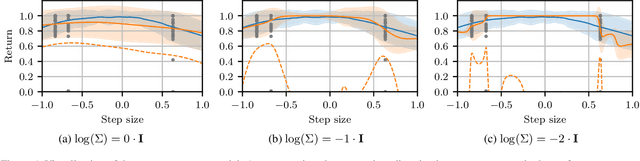
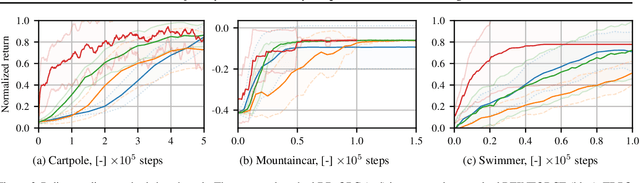
Policy gradient methods are powerful reinforcement learning algorithms and have been demonstrated to solve many complex tasks. However, these methods are also data-inefficient, afflicted with high variance gradient estimates, and frequently get stuck in local optima. This work addresses these weaknesses by combining recent improvements in the reuse of off-policy data and exploration in parameter space with deterministic behavioral policies. The resulting objective is amenable to standard neural network optimization strategies like stochastic gradient descent or stochastic gradient Hamiltonian Monte Carlo. Incorporation of previous rollouts via importance sampling greatly improves data-efficiency, whilst stochastic optimization schemes facilitate the escape from local optima. We evaluate the proposed approach on a series of continuous control benchmark tasks. The results show that the proposed algorithm is able to successfully and reliably learn solutions using fewer system interactions than standard policy gradient methods.

Meta-Learning Acquisition Functions for Bayesian Optimization

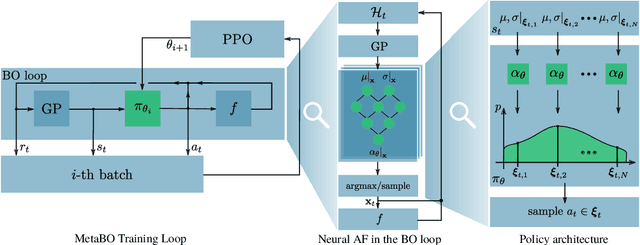
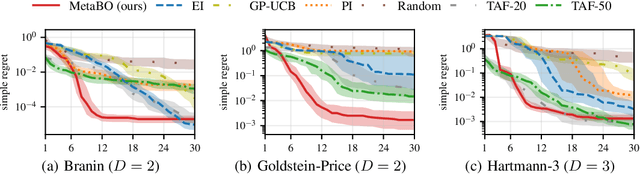
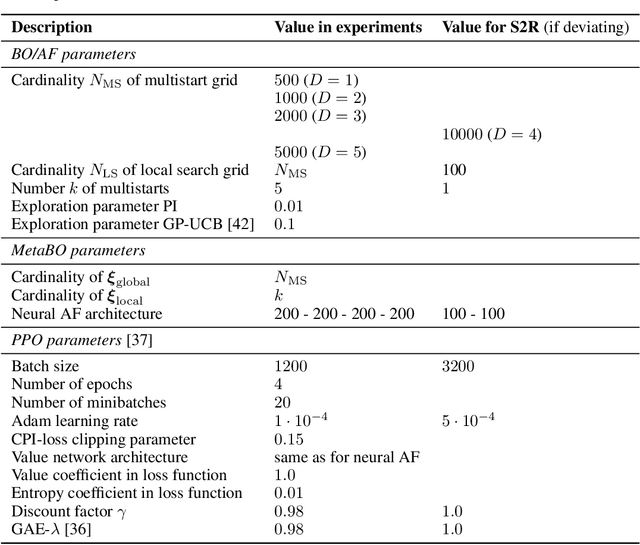
Many practical applications of machine learning require data-efficient black-box function optimization, e.g., to identify hyperparameters or process settings. However, readily available algorithms are typically designed to be universal optimizers and are, thus, often suboptimal for specific tasks. We therefore propose a method to learn optimizers which are automatically adapted to a given class of objective functions, e.g., in the context of sim-to-real applications. Instead of learning optimization from scratch, the proposed approach is firmly based within the famous Bayesian optimization framework. Only the acquisition function (AF) is replaced by a learned neural network and therefore the resulting algorithm is still able to exploit the proven generalization capabilities of Gaussian processes. We present experiments on several simulated as well as on a sim-to-real transfer task. The results show that the learned optimizers (1) consistently perform better than or on-par with known AFs on general function classes and (2) can automatically identify structural properties of a function class using cheap simulations and transfer this knowledge to adapt rapidly to real hardware tasks, thereby significantly outperforming existing problem-agnostic AFs.