Philipp Dahlinger
Context-aware Learned Mesh-based Simulation via Trajectory-Level Meta-Learning
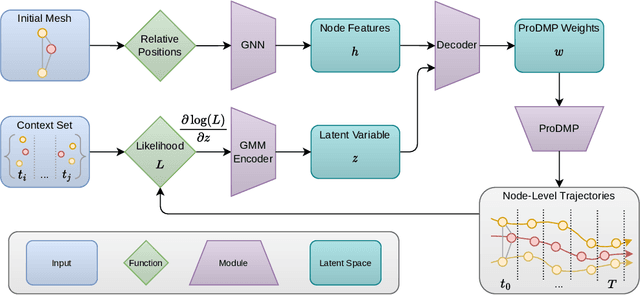
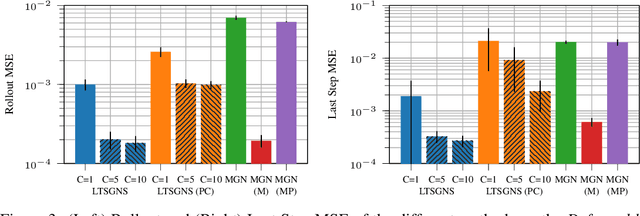
Nov 07, 2025Abstract:Simulating object deformations is a critical challenge across many scientific domains, including robotics, manufacturing, and structural mechanics. Learned Graph Network Simulators (GNSs) offer a promising alternative to traditional mesh-based physics simulators. Their speed and inherent differentiability make them particularly well suited for applications that require fast and accurate simulations, such as robotic manipulation or manufacturing optimization. However, existing learned simulators typically rely on single-step observations, which limits their ability to exploit temporal context. Without this information, these models fail to infer, e.g., material properties. Further, they rely on auto-regressive rollouts, which quickly accumulate error for long trajectories. We instead frame mesh-based simulation as a trajectory-level meta-learning problem. Using Conditional Neural Processes, our method enables rapid adaptation to new simulation scenarios from limited initial data while capturing their latent simulation properties. We utilize movement primitives to directly predict fast, stable and accurate simulations from a single model call. The resulting approach, Movement-primitive Meta-MeshGraphNet (M3GN), provides higher simulation accuracy at a fraction of the runtime cost compared to state-of-the-art GNSs across several tasks.
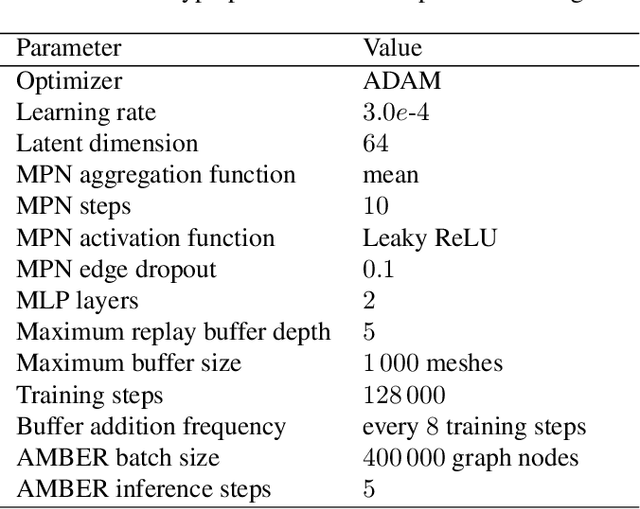
AMBER: Adaptive Mesh Generation by Iterative Mesh Resolution Prediction
May 29, 2025Abstract:The cost and accuracy of simulating complex physical systems using the Finite Element Method (FEM) scales with the resolution of the underlying mesh. Adaptive meshes improve computational efficiency by refining resolution in critical regions, but typically require task-specific heuristics or cumbersome manual design by a human expert. We propose Adaptive Meshing By Expert Reconstruction (AMBER), a supervised learning approach to mesh adaptation. Starting from a coarse mesh, AMBER iteratively predicts the sizing field, i.e., a function mapping from the geometry to the local element size of the target mesh, and uses this prediction to produce a new intermediate mesh using an out-of-the-box mesh generator. This process is enabled through a hierarchical graph neural network, and relies on data augmentation by automatically projecting expert labels onto AMBER-generated data during training. We evaluate AMBER on 2D and 3D datasets, including classical physics problems, mechanical components, and real-world industrial designs with human expert meshes. AMBER generalizes to unseen geometries and consistently outperforms multiple recent baselines, including ones using Graph and Convolutional Neural Networks, and Reinforcement Learning-based approaches.
Beyond Task Performance: Human Experience in Human-Robot Collaboration
May 07, 2025Abstract:Human interaction experience plays a crucial role in the effectiveness of human-machine collaboration, especially as interactions in future systems progress towards tighter physical and functional integration. While automation design has been shown to impact task performance, its influence on human experience metrics such as flow, sense of agency (SoA), and embodiment remains underexplored. This study investigates how variations in automation design affect these psychological experience measures and examines correlations between subjective experience and physiological indicators. A user study was conducted in a simulated wood workshop, where participants collaborated with a lightweight robot under four automation levels. The results of the study indicate that medium automation levels enhance flow, SoA and embodiment, striking a balance between support and user autonomy. In contrast, higher automation, despite optimizing task performance, diminishes perceived flow and agency. Furthermore, we observed that grip force might be considered as a real-time proxy of SoA, while correlations with heart rate variability were inconclusive. The findings underscore the necessity for automation strategies that integrate human- centric metrics, aiming to optimize both performance and user experience in collaborative robotic systems
Beyond Visuals: Investigating Force Feedback in Extended Reality for Robot Data Collection
Mar 26, 2025Abstract:This work explores how force feedback affects various aspects of robot data collection within the Extended Reality (XR) setting. Force feedback has been proved to enhance the user experience in Extended Reality (XR) by providing contact-rich information. However, its impact on robot data collection has not received much attention in the robotics community. This paper addresses this shortcoming by conducting an extensive user study on the effects of force feedback during data collection in XR. We extended two XR-based robot control interfaces, Kinesthetic Teaching and Motion Controllers, with haptic feedback features. The user study is conducted using manipulation tasks ranging from simple pick-place to complex peg assemble, requiring precise operations. The evaluations show that force feedback enhances task performance and user experience, particularly in tasks requiring high-precision manipulation. These improvements vary depending on the robot control interface and task complexity. This paper provides new insights into how different factors influence the impact of force feedback.
Iterative Sizing Field Prediction for Adaptive Mesh Generation From Expert Demonstrations
Jun 20, 2024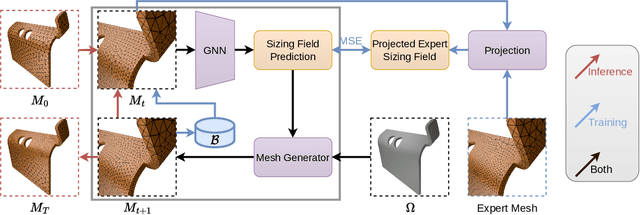
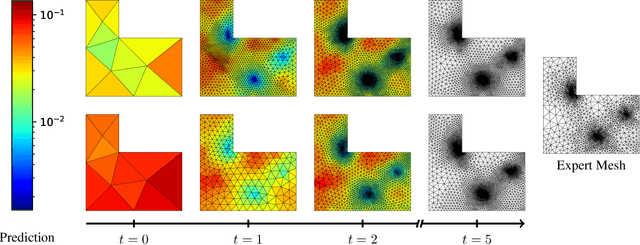
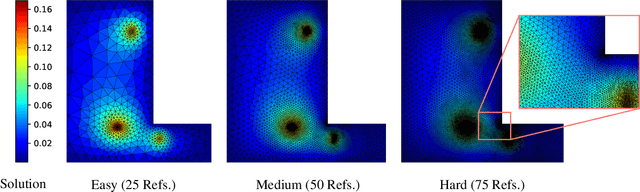
Abstract:Many engineering systems require accurate simulations of complex physical systems. Yet, analytical solutions are only available for simple problems, necessitating numerical approximations such as the Finite Element Method (FEM). The cost and accuracy of the FEM scale with the resolution of the underlying computational mesh. To balance computational speed and accuracy meshes with adaptive resolution are used, allocating more resources to critical parts of the geometry. Currently, practitioners often resort to hand-crafted meshes, which require extensive expert knowledge and are thus costly to obtain. Our approach, Adaptive Meshing By Expert Reconstruction (AMBER), views mesh generation as an imitation learning problem. AMBER combines a graph neural network with an online data acquisition scheme to predict the projected sizing field of an expert mesh on a given intermediate mesh, creating a more accurate subsequent mesh. This iterative process ensures efficient and accurate imitation of expert mesh resolutions on arbitrary new geometries during inference. We experimentally validate AMBER on heuristic 2D meshes and 3D meshes provided by a human expert, closely matching the provided demonstrations and outperforming a single-step CNN baseline.
Adaptive Swarm Mesh Refinement using Deep Reinforcement Learning with Local Rewards
Jun 12, 2024Abstract:Simulating physical systems is essential in engineering, but analytical solutions are limited to straightforward problems. Consequently, numerical methods like the Finite Element Method (FEM) are widely used. However, the FEM becomes computationally expensive as problem complexity and accuracy demands increase. Adaptive Mesh Refinement (AMR) improves the FEM by dynamically allocating mesh elements on the domain, balancing computational speed and accuracy. Classical AMR depends on heuristics or expensive error estimators, limiting its use in complex simulations. While learning-based AMR methods are promising, they currently only scale to simple problems. In this work, we formulate AMR as a system of collaborating, homogeneous agents that iteratively split into multiple new agents. This agent-wise perspective enables a spatial reward formulation focused on reducing the maximum mesh element error. Our approach, Adaptive Swarm Mesh Refinement (ASMR), offers efficient, stable optimization and generates highly adaptive meshes at user-defined resolution during inference. Extensive experiments, including volumetric meshes and Neumann boundary conditions, demonstrate that ASMR exceeds heuristic approaches and learned baselines, matching the performance of expensive error-based oracle AMR strategies. ASMR additionally generalizes to different domains during inference, and produces meshes that simulate up to 2 orders of magnitude faster than uniform refinements in more demanding settings.
Latent Task-Specific Graph Network Simulators
Nov 09, 2023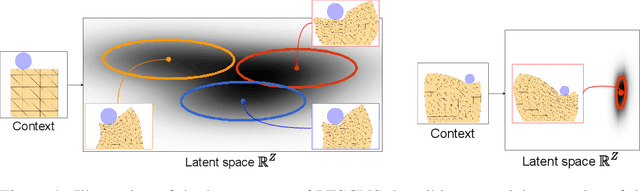

Abstract:Simulating dynamic physical interactions is a critical challenge across multiple scientific domains, with applications ranging from robotics to material science. For mesh-based simulations, Graph Network Simulators (GNSs) pose an efficient alternative to traditional physics-based simulators. Their inherent differentiability and speed make them particularly well-suited for inverse design problems. Yet, adapting to new tasks from limited available data is an important aspect for real-world applications that current methods struggle with. We frame mesh-based simulation as a meta-learning problem and use a recent Bayesian meta-learning method to improve GNSs adaptability to new scenarios by leveraging context data and handling uncertainties. Our approach, latent task-specific graph network simulator, uses non-amortized task posterior approximations to sample latent descriptions of unknown system properties. Additionally, we leverage movement primitives for efficient full trajectory prediction, effectively addressing the issue of accumulating errors encountered by previous auto-regressive methods. We validate the effectiveness of our approach through various experiments, performing on par with or better than established baseline methods. Movement primitives further allow us to accommodate various types of context data, as demonstrated through the utilization of point clouds during inference. By combining GNSs with meta-learning, we bring them closer to real-world applicability, particularly in scenarios with smaller datasets.
Information-Theoretic Trust Regions for Stochastic Gradient-Based Optimization
Oct 31, 2023Abstract:Stochastic gradient-based optimization is crucial to optimize neural networks. While popular approaches heuristically adapt the step size and direction by rescaling gradients, a more principled approach to improve optimizers requires second-order information. Such methods precondition the gradient using the objective's Hessian. Yet, computing the Hessian is usually expensive and effectively using second-order information in the stochastic gradient setting is non-trivial. We propose using Information-Theoretic Trust Region Optimization (arTuRO) for improved updates with uncertain second-order information. By modeling the network parameters as a Gaussian distribution and using a Kullback-Leibler divergence-based trust region, our approach takes bounded steps accounting for the objective's curvature and uncertainty in the parameters. Before each update, it solves the trust region problem for an optimal step size, resulting in a more stable and faster optimization process. We approximate the diagonal elements of the Hessian from stochastic gradients using a simple recursive least squares approach, constructing a model of the expected Hessian over time using only first-order information. We show that arTuRO combines the fast convergence of adaptive moment-based optimization with the generalization capabilities of SGD.
Swarm Reinforcement Learning For Adaptive Mesh Refinement
Apr 03, 2023



Abstract:Adaptive Mesh Refinement (AMR) is crucial for mesh-based simulations, as it allows for dynamically adjusting the resolution of a mesh to trade off computational cost with the simulation accuracy. Yet, existing methods for AMR either use task-dependent heuristics, expensive error estimators, or do not scale well to larger meshes or more complex problems. In this paper, we formalize AMR as a Swarm Reinforcement Learning problem, viewing each element of a mesh as part of a collaborative system of simple and homogeneous agents. We combine this problem formulation with a novel agent-wise reward function and Graph Neural Networks, allowing us to learn reliable and scalable refinement strategies on arbitrary systems of equations. We experimentally demonstrate the effectiveness of our approach in improving the accuracy and efficiency of complex simulations. Our results show that we outperform learned baselines and achieve a refinement quality that is on par with a traditional error-based AMR refinement strategy without requiring error indicators during inference.
A Unified Perspective on Natural Gradient Variational Inference with Gaussian Mixture Models
Sep 23, 2022



Abstract:Variational inference with Gaussian mixture models (GMMs) enables learning of highly-tractable yet multi-modal approximations of intractable target distributions. GMMs are particular relevant for problem settings with up to a few hundred dimensions, for example in robotics, for modelling distributions over trajectories or joint distributions. This work focuses on two very effective methods for GMM-based variational inference that both employ independent natural gradient updates for the individual components and the categorical distribution of the weights. We show for the first time, that their derived updates are equivalent, although their practical implementations and theoretical guarantees differ. We identify several design choices that distinguish both approaches, namely with respect to sample selection, natural gradient estimation, stepsize adaptation, and whether trust regions are enforced or the number of components adapted. We perform extensive ablations on these design choices and show that they strongly affect the efficiency of the optimization and the variability of the learned distribution. Based on our insights, we propose a novel instantiation of our generalized framework, that combines first-order natural gradient estimates with trust-regions and component adaption, and significantly outperforms both previous methods in all our experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge