Luise Kärger
Iterative Sizing Field Prediction for Adaptive Mesh Generation From Expert Demonstrations
Jun 20, 2024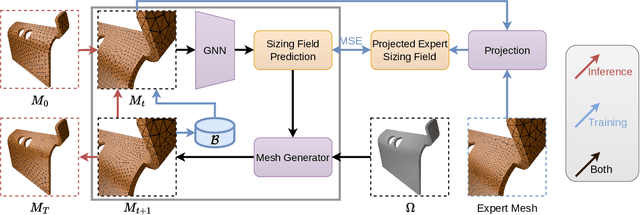
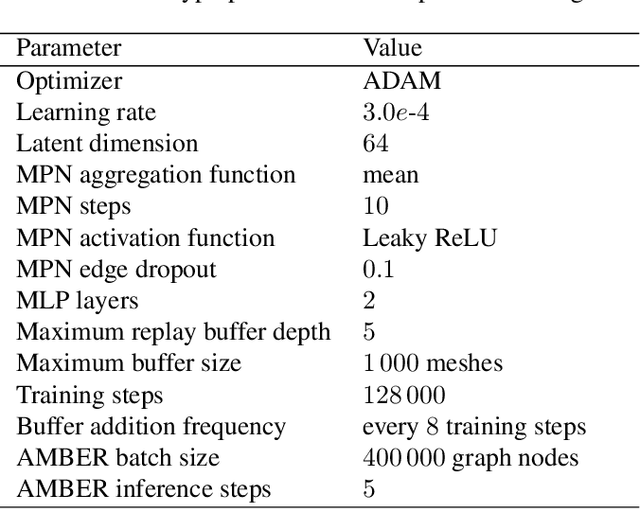
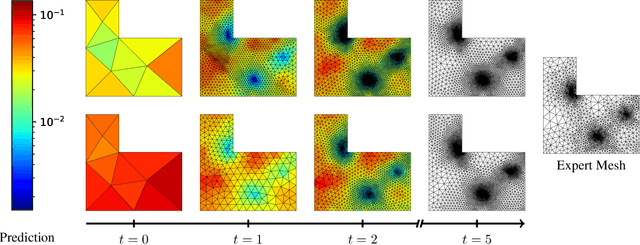
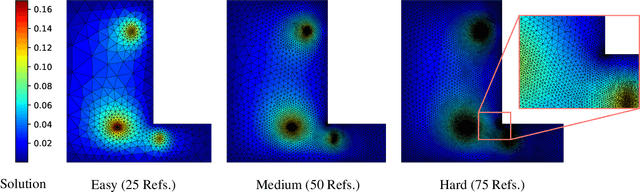
Abstract:Many engineering systems require accurate simulations of complex physical systems. Yet, analytical solutions are only available for simple problems, necessitating numerical approximations such as the Finite Element Method (FEM). The cost and accuracy of the FEM scale with the resolution of the underlying computational mesh. To balance computational speed and accuracy meshes with adaptive resolution are used, allocating more resources to critical parts of the geometry. Currently, practitioners often resort to hand-crafted meshes, which require extensive expert knowledge and are thus costly to obtain. Our approach, Adaptive Meshing By Expert Reconstruction (AMBER), views mesh generation as an imitation learning problem. AMBER combines a graph neural network with an online data acquisition scheme to predict the projected sizing field of an expert mesh on a given intermediate mesh, creating a more accurate subsequent mesh. This iterative process ensures efficient and accurate imitation of expert mesh resolutions on arbitrary new geometries during inference. We experimentally validate AMBER on heuristic 2D meshes and 3D meshes provided by a human expert, closely matching the provided demonstrations and outperforming a single-step CNN baseline.
Adaptive Swarm Mesh Refinement using Deep Reinforcement Learning with Local Rewards
Jun 12, 2024Abstract:Simulating physical systems is essential in engineering, but analytical solutions are limited to straightforward problems. Consequently, numerical methods like the Finite Element Method (FEM) are widely used. However, the FEM becomes computationally expensive as problem complexity and accuracy demands increase. Adaptive Mesh Refinement (AMR) improves the FEM by dynamically allocating mesh elements on the domain, balancing computational speed and accuracy. Classical AMR depends on heuristics or expensive error estimators, limiting its use in complex simulations. While learning-based AMR methods are promising, they currently only scale to simple problems. In this work, we formulate AMR as a system of collaborating, homogeneous agents that iteratively split into multiple new agents. This agent-wise perspective enables a spatial reward formulation focused on reducing the maximum mesh element error. Our approach, Adaptive Swarm Mesh Refinement (ASMR), offers efficient, stable optimization and generates highly adaptive meshes at user-defined resolution during inference. Extensive experiments, including volumetric meshes and Neumann boundary conditions, demonstrate that ASMR exceeds heuristic approaches and learned baselines, matching the performance of expensive error-based oracle AMR strategies. ASMR additionally generalizes to different domains during inference, and produces meshes that simulate up to 2 orders of magnitude faster than uniform refinements in more demanding settings.
Physics-informed MeshGraphNets (PI-MGNs): Neural finite element solvers for non-stationary and nonlinear simulations on arbitrary meshes
Feb 16, 2024



Abstract:Engineering components must meet increasing technological demands in ever shorter development cycles. To face these challenges, a holistic approach is essential that allows for the concurrent development of part design, material system and manufacturing process. Current approaches employ numerical simulations, which however quickly becomes computation-intensive, especially for iterative optimization. Data-driven machine learning methods can be used to replace time- and resource-intensive numerical simulations. In particular, MeshGraphNets (MGNs) have shown promising results. They enable fast and accurate predictions on unseen mesh geometries while being fully differentiable for optimization. However, these models rely on large amounts of expensive training data, such as numerical simulations. Physics-informed neural networks (PINNs) offer an opportunity to train neural networks with partial differential equations instead of labeled data, but have not been extended yet to handle time-dependent simulations of arbitrary meshes. This work introduces PI-MGNs, a hybrid approach that combines PINNs and MGNs to quickly and accurately solve non-stationary and nonlinear partial differential equations (PDEs) on arbitrary meshes. The method is exemplified for thermal process simulations of unseen parts with inhomogeneous material distribution. Further results show that the model scales well to large and complex meshes, although it is trained on small generic meshes only.
Swarm Reinforcement Learning For Adaptive Mesh Refinement
Apr 03, 2023



Abstract:Adaptive Mesh Refinement (AMR) is crucial for mesh-based simulations, as it allows for dynamically adjusting the resolution of a mesh to trade off computational cost with the simulation accuracy. Yet, existing methods for AMR either use task-dependent heuristics, expensive error estimators, or do not scale well to larger meshes or more complex problems. In this paper, we formalize AMR as a Swarm Reinforcement Learning problem, viewing each element of a mesh as part of a collaborative system of simple and homogeneous agents. We combine this problem formulation with a novel agent-wise reward function and Graph Neural Networks, allowing us to learn reliable and scalable refinement strategies on arbitrary systems of equations. We experimentally demonstrate the effectiveness of our approach in improving the accuracy and efficiency of complex simulations. Our results show that we outperform learned baselines and achieve a refinement quality that is on par with a traditional error-based AMR refinement strategy without requiring error indicators during inference.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge