Improving Long-Range Interactions in Graph Neural Simulators via Hamiltonian Dynamics

Learning to simulate complex physical systems from data has emerged as a promising way to overcome the limitations of traditional numerical solvers, which often require prohibitive computational costs for high-fidelity solutions. Recent Graph Neural Simulators (GNSs) accelerate simulations by learning dynamics on graph-structured data, yet often struggle to capture long-range interactions and suffer from error accumulation under autoregressive rollouts. To address these challenges, we propose Information-preserving Graph Neural Simulators (IGNS), a graph-based neural simulator built on the principles of Hamiltonian dynamics. This structure guarantees preservation of information across the graph, while extending to port-Hamiltonian systems allows the model to capture a broader class of dynamics, including non-conservative effects. IGNS further incorporates a warmup phase to initialize global context, geometric encoding to handle irregular meshes, and a multi-step training objective to reduce rollout error. To evaluate these properties systematically, we introduce new benchmarks that target long-range dependencies and challenging external forcing scenarios. Across all tasks, IGNS consistently outperforms state-of-the-art GNSs, achieving higher accuracy and stability under challenging and complex dynamical systems.

Context-aware Learned Mesh-based Simulation via Trajectory-Level Meta-Learning

Simulating object deformations is a critical challenge across many scientific domains, including robotics, manufacturing, and structural mechanics. Learned Graph Network Simulators (GNSs) offer a promising alternative to traditional mesh-based physics simulators. Their speed and inherent differentiability make them particularly well suited for applications that require fast and accurate simulations, such as robotic manipulation or manufacturing optimization. However, existing learned simulators typically rely on single-step observations, which limits their ability to exploit temporal context. Without this information, these models fail to infer, e.g., material properties. Further, they rely on auto-regressive rollouts, which quickly accumulate error for long trajectories. We instead frame mesh-based simulation as a trajectory-level meta-learning problem. Using Conditional Neural Processes, our method enables rapid adaptation to new simulation scenarios from limited initial data while capturing their latent simulation properties. We utilize movement primitives to directly predict fast, stable and accurate simulations from a single model call. The resulting approach, Movement-primitive Meta-MeshGraphNet (M3GN), provides higher simulation accuracy at a fraction of the runtime cost compared to state-of-the-art GNSs across several tasks.

Diffusion-Based Hierarchical Graph Neural Networks for Simulating Nonlinear Solid Mechanics

Graph-based learned simulators have emerged as a promising approach for simulating physical systems on unstructured meshes, offering speed and generalization across diverse geometries. However, they often struggle with capturing global phenomena, such as bending or long-range correlations, and suffer from error accumulation over long rollouts due to their reliance on local message passing and direct next-step prediction. We address these limitations by introducing the Rolling Diffusion-Batched Inference Network (ROBIN), a novel learned simulator that integrates two key innovations: (i) Rolling Diffusion, a parallelized inference scheme that amortizes the cost of diffusion-based refinement across physical time steps by overlapping denoising steps across a temporal window. (ii) A Hierarchical Graph Neural Network built on algebraic multigrid coarsening, enabling multiscale message passing across different mesh resolutions. This architecture, implemented via Algebraic-hierarchical Message Passing Networks, captures both fine-scale local dynamics and global structural effects critical for phenomena like beam bending or multi-body contact. We validate ROBIN on challenging 2D and 3D solid mechanics benchmarks involving geometric, material, and contact nonlinearities. ROBIN achieves state-of-the-art accuracy on all tasks, substantially outperforming existing next-step learned simulators while reducing inference time by up to an order of magnitude compared to standard diffusion simulators.

AMBER: Adaptive Mesh Generation by Iterative Mesh Resolution Prediction

The cost and accuracy of simulating complex physical systems using the Finite Element Method (FEM) scales with the resolution of the underlying mesh. Adaptive meshes improve computational efficiency by refining resolution in critical regions, but typically require task-specific heuristics or cumbersome manual design by a human expert. We propose Adaptive Meshing By Expert Reconstruction (AMBER), a supervised learning approach to mesh adaptation. Starting from a coarse mesh, AMBER iteratively predicts the sizing field, i.e., a function mapping from the geometry to the local element size of the target mesh, and uses this prediction to produce a new intermediate mesh using an out-of-the-box mesh generator. This process is enabled through a hierarchical graph neural network, and relies on data augmentation by automatically projecting expert labels onto AMBER-generated data during training. We evaluate AMBER on 2D and 3D datasets, including classical physics problems, mechanical components, and real-world industrial designs with human expert meshes. AMBER generalizes to unseen geometries and consistently outperforms multiple recent baselines, including ones using Graph and Convolutional Neural Networks, and Reinforcement Learning-based approaches.

Hierarchical Multi-field Representations for Two-Stage E-commerce Retrieval

Dense retrieval methods typically target unstructured text data represented as flat strings. However, e-commerce catalogs often include structured information across multiple fields, such as brand, title, and description, which contain important information potential for retrieval systems. We present Cascading Hierarchical Attention Retrieval Model (CHARM), a novel framework designed to encode structured product data into hierarchical field-level representations with progressively finer detail. Utilizing a novel block-triangular attention mechanism, our method captures the interdependencies between product fields in a specified hierarchy, yielding field-level representations and aggregated vectors suitable for fast and efficient retrieval. Combining both representations enables a two-stage retrieval pipeline, in which the aggregated vectors support initial candidate selection, while more expressive field-level representations facilitate precise fine-tuning for downstream ranking. Experiments on publicly available large-scale e-commerce datasets demonstrate that CHARM matches or outperforms state-of-the-art baselines. Our analysis highlights the framework's ability to align different queries with appropriate product fields, enhancing retrieval accuracy and explainability.

Learning Sub-Second Routing Optimization in Computer Networks requires Packet-Level Dynamics

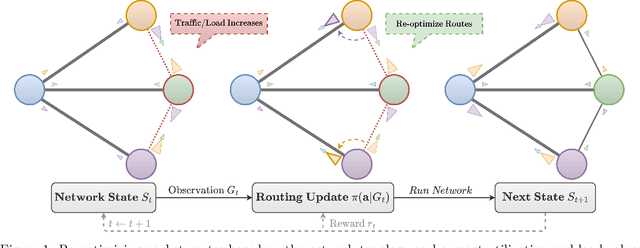
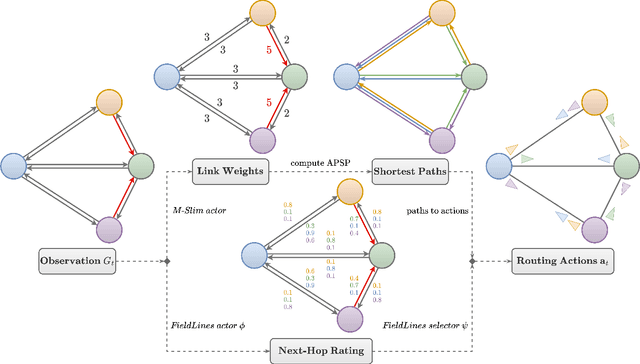
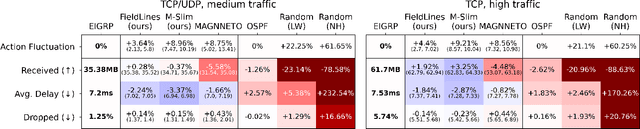
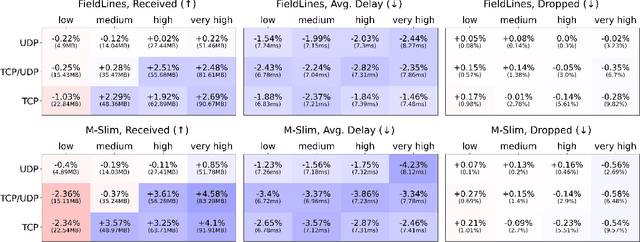
Finding efficient routes for data packets is an essential task in computer networking. The optimal routes depend greatly on the current network topology, state and traffic demand, and they can change within milliseconds. Reinforcement Learning can help to learn network representations that provide routing decisions for possibly novel situations. So far, this has commonly been done using fluid network models. We investigate their suitability for millisecond-scale adaptations with a range of traffic mixes and find that packet-level network models are necessary to capture true dynamics, in particular in the presence of TCP traffic. To this end, we present $\textit{PackeRL}$, the first packet-level Reinforcement Learning environment for routing in generic network topologies. Our experiments confirm that learning-based strategies that have been trained in fluid environments do not generalize well to this more realistic, but more challenging setup. Hence, we also introduce two new algorithms for learning sub-second Routing Optimization. We present $\textit{M-Slim}$, a dynamic shortest-path algorithm that excels at high traffic volumes but is computationally hard to scale to large network topologies, and $\textit{FieldLines}$, a novel next-hop policy design that re-optimizes routing for any network topology within milliseconds without requiring any re-training. Both algorithms outperform current learning-based approaches as well as commonly used static baseline protocols in scenarios with high-traffic volumes. All findings are backed by extensive experiments in realistic network conditions in our fast and versatile training and evaluation framework.

KalMamba: Towards Efficient Probabilistic State Space Models for RL under Uncertainty

Probabilistic State Space Models (SSMs) are essential for Reinforcement Learning (RL) from high-dimensional, partial information as they provide concise representations for control. Yet, they lack the computational efficiency of their recent deterministic counterparts such as S4 or Mamba. We propose KalMamba, an efficient architecture to learn representations for RL that combines the strengths of probabilistic SSMs with the scalability of deterministic SSMs. KalMamba leverages Mamba to learn the dynamics parameters of a linear Gaussian SSM in a latent space. Inference in this latent space amounts to standard Kalman filtering and smoothing. We realize these operations using parallel associative scanning, similar to Mamba, to obtain a principled, highly efficient, and scalable probabilistic SSM. Our experiments show that KalMamba competes with state-of-the-art SSM approaches in RL while significantly improving computational efficiency, especially on longer interaction sequences.

Iterative Sizing Field Prediction for Adaptive Mesh Generation From Expert Demonstrations

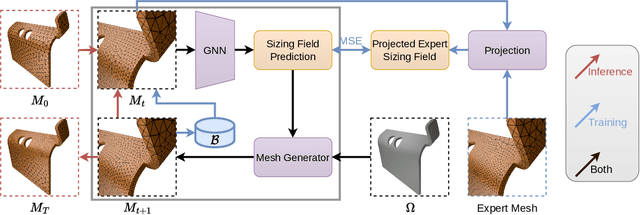
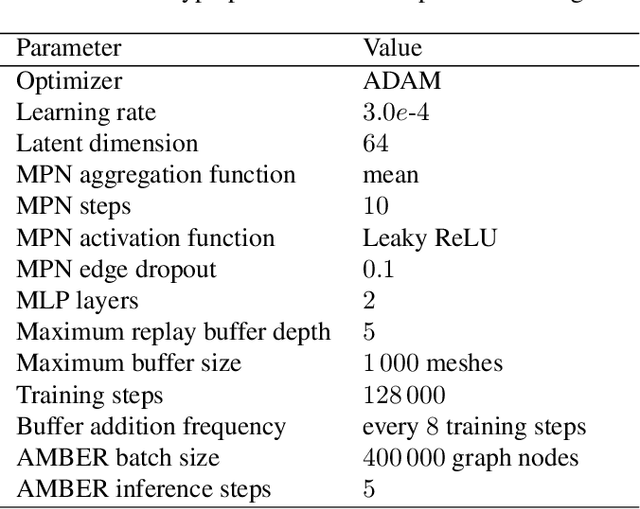
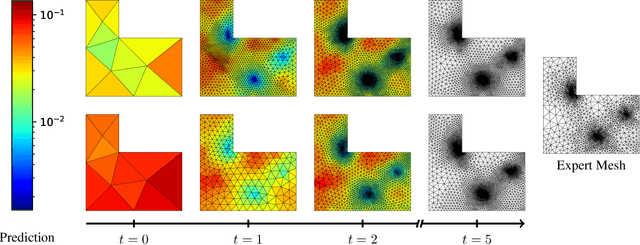
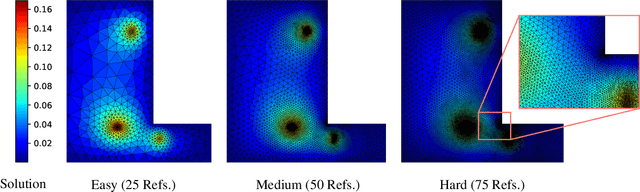
Many engineering systems require accurate simulations of complex physical systems. Yet, analytical solutions are only available for simple problems, necessitating numerical approximations such as the Finite Element Method (FEM). The cost and accuracy of the FEM scale with the resolution of the underlying computational mesh. To balance computational speed and accuracy meshes with adaptive resolution are used, allocating more resources to critical parts of the geometry. Currently, practitioners often resort to hand-crafted meshes, which require extensive expert knowledge and are thus costly to obtain. Our approach, Adaptive Meshing By Expert Reconstruction (AMBER), views mesh generation as an imitation learning problem. AMBER combines a graph neural network with an online data acquisition scheme to predict the projected sizing field of an expert mesh on a given intermediate mesh, creating a more accurate subsequent mesh. This iterative process ensures efficient and accurate imitation of expert mesh resolutions on arbitrary new geometries during inference. We experimentally validate AMBER on heuristic 2D meshes and 3D meshes provided by a human expert, closely matching the provided demonstrations and outperforming a single-step CNN baseline.

Adaptive Swarm Mesh Refinement using Deep Reinforcement Learning with Local Rewards

Simulating physical systems is essential in engineering, but analytical solutions are limited to straightforward problems. Consequently, numerical methods like the Finite Element Method (FEM) are widely used. However, the FEM becomes computationally expensive as problem complexity and accuracy demands increase. Adaptive Mesh Refinement (AMR) improves the FEM by dynamically allocating mesh elements on the domain, balancing computational speed and accuracy. Classical AMR depends on heuristics or expensive error estimators, limiting its use in complex simulations. While learning-based AMR methods are promising, they currently only scale to simple problems. In this work, we formulate AMR as a system of collaborating, homogeneous agents that iteratively split into multiple new agents. This agent-wise perspective enables a spatial reward formulation focused on reducing the maximum mesh element error. Our approach, Adaptive Swarm Mesh Refinement (ASMR), offers efficient, stable optimization and generates highly adaptive meshes at user-defined resolution during inference. Extensive experiments, including volumetric meshes and Neumann boundary conditions, demonstrate that ASMR exceeds heuristic approaches and learned baselines, matching the performance of expensive error-based oracle AMR strategies. ASMR additionally generalizes to different domains during inference, and produces meshes that simulate up to 2 orders of magnitude faster than uniform refinements in more demanding settings.

Physics-informed MeshGraphNets (PI-MGNs): Neural finite element solvers for non-stationary and nonlinear simulations on arbitrary meshes

Engineering components must meet increasing technological demands in ever shorter development cycles. To face these challenges, a holistic approach is essential that allows for the concurrent development of part design, material system and manufacturing process. Current approaches employ numerical simulations, which however quickly becomes computation-intensive, especially for iterative optimization. Data-driven machine learning methods can be used to replace time- and resource-intensive numerical simulations. In particular, MeshGraphNets (MGNs) have shown promising results. They enable fast and accurate predictions on unseen mesh geometries while being fully differentiable for optimization. However, these models rely on large amounts of expensive training data, such as numerical simulations. Physics-informed neural networks (PINNs) offer an opportunity to train neural networks with partial differential equations instead of labeled data, but have not been extended yet to handle time-dependent simulations of arbitrary meshes. This work introduces PI-MGNs, a hybrid approach that combines PINNs and MGNs to quickly and accurately solve non-stationary and nonlinear partial differential equations (PDEs) on arbitrary meshes. The method is exemplified for thermal process simulations of unseen parts with inhomogeneous material distribution. Further results show that the model scales well to large and complex meshes, although it is trained on small generic meshes only.