IRIS: An Immersive Robot Interaction System

This paper introduces IRIS, an immersive Robot Interaction System leveraging Extended Reality (XR), designed for robot data collection and interaction across multiple simulators, benchmarks, and real-world scenarios. While existing XR-based data collection systems provide efficient and intuitive solutions for large-scale data collection, they are often challenging to reproduce and reuse. This limitation arises because current systems are highly tailored to simulator-specific use cases and environments. IRIS is a novel, easily extendable framework that already supports multiple simulators, benchmarks, and even headsets. Furthermore, IRIS is able to include additional information from real-world sensors, such as point clouds captured through depth cameras. A unified scene specification is generated directly from simulators or real-world sensors and transmitted to XR headsets, creating identical scenes in XR. This specification allows IRIS to support any of the objects, assets, and robots provided by the simulators. In addition, IRIS introduces shared spatial anchors and a robust communication protocol that links simulations between multiple XR headsets. This feature enables multiple XR headsets to share a synchronized scene, facilitating collaborative and multi-user data collection. IRIS can be deployed on any device that supports the Unity Framework, encompassing the vast majority of commercially available headsets. In this work, IRIS was deployed and tested on the Meta Quest 3 and the HoloLens 2. IRIS showcased its versatility across a wide range of real-world and simulated scenarios, using current popular robot simulators such as MuJoCo, IsaacSim, CoppeliaSim, and Genesis. In addition, a user study evaluates IRIS on a data collection task for the LIBERO benchmark. The study shows that IRIS significantly outperforms the baseline in both objective and subjective metrics.

Movement Primitive Diffusion: Learning Gentle Robotic Manipulation of Deformable Objects

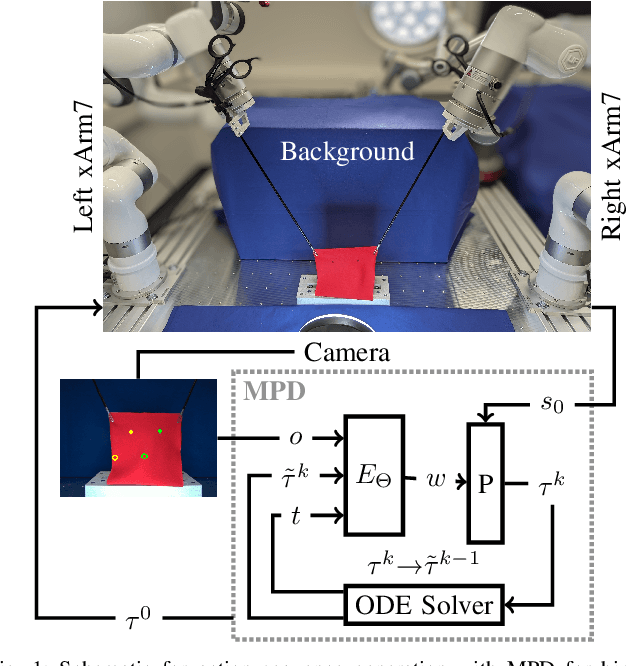
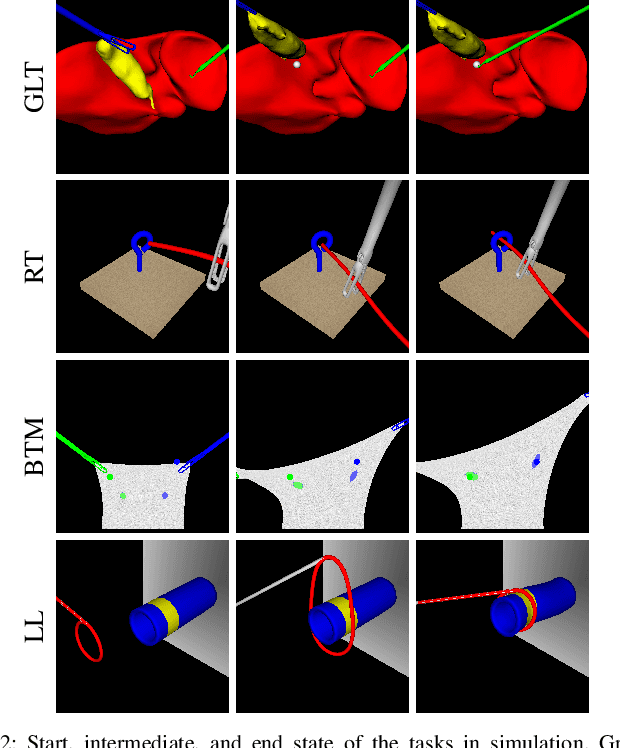
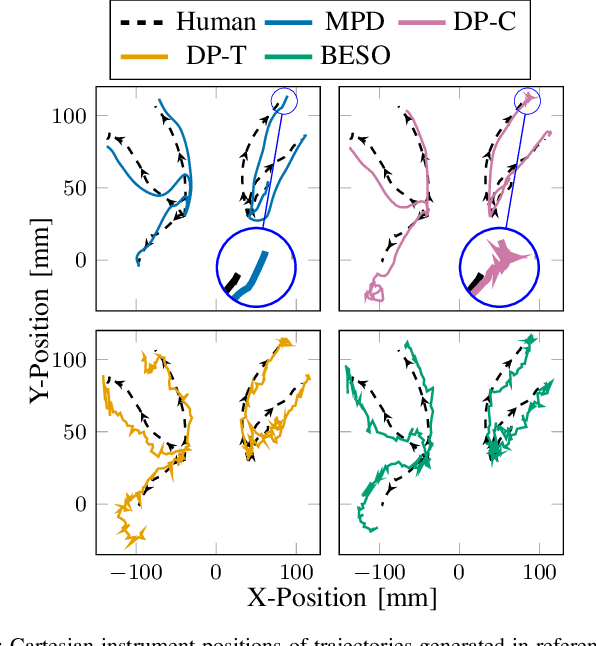
Policy learning in robot-assisted surgery (RAS) lacks data efficient and versatile methods that exhibit the desired motion quality for delicate surgical interventions. To this end, we introduce Movement Primitive Diffusion (MPD), a novel method for imitation learning (IL) in RAS that focuses on gentle manipulation of deformable objects. The approach combines the versatility of diffusion-based imitation learning (DIL) with the high-quality motion generation capabilities of Probabilistic Dynamic Movement Primitives (ProDMPs). This combination enables MPD to achieve gentle manipulation of deformable objects, while maintaining data efficiency critical for RAS applications where demonstration data is scarce. We evaluate MPD across various simulated tasks and a real world robotic setup on both state and image observations. MPD outperforms state-of-the-art DIL methods in success rate, motion quality, and data efficiency.

Inferring Versatile Behavior from Demonstrations by Matching Geometric Descriptors

Humans intuitively solve tasks in versatile ways, varying their behavior in terms of trajectory-based planning and for individual steps. Thus, they can easily generalize and adapt to new and changing environments. Current Imitation Learning algorithms often only consider unimodal expert demonstrations and act in a state-action-based setting, making it difficult for them to imitate human behavior in case of versatile demonstrations. Instead, we combine a mixture of movement primitives with a distribution matching objective to learn versatile behaviors that match the expert's behavior and versatility. To facilitate generalization to novel task configurations, we do not directly match the agent's and expert's trajectory distributions but rather work with concise geometric descriptors which generalize well to unseen task configurations. We empirically validate our method on various robot tasks using versatile human demonstrations and compare to imitation learning algorithms in a state-action setting as well as a trajectory-based setting. We find that the geometric descriptors greatly help in generalizing to new task configurations and that combining them with our distribution-matching objective is crucial for representing and reproducing versatile behavior.