Kailai Li
REASAN: Learning Reactive Safe Navigation for Legged Robots
Dec 10, 2025

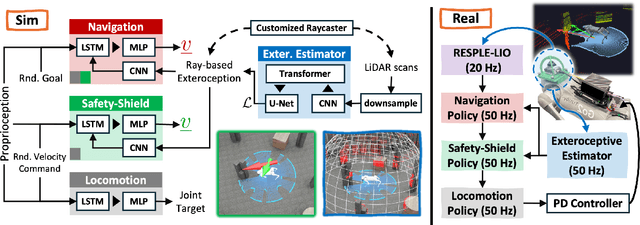
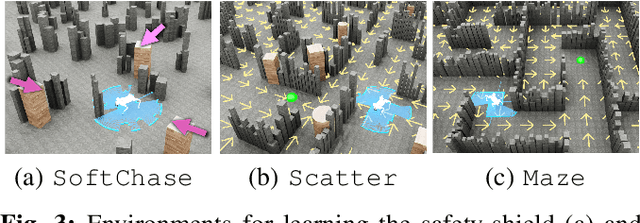
Abstract:We present a novel modularized end-to-end framework for legged reactive navigation in complex dynamic environments using a single light detection and ranging (LiDAR) sensor. The system comprises four simulation-trained modules: three reinforcement-learning (RL) policies for locomotion, safety shielding, and navigation, and a transformer-based exteroceptive estimator that processes raw point-cloud inputs. This modular decomposition of complex legged motor-control tasks enables lightweight neural networks with simple architectures, trained using standard RL practices with targeted reward shaping and curriculum design, without reliance on heuristics or sophisticated policy-switching mechanisms. We conduct comprehensive ablations to validate our design choices and demonstrate improved robustness compared to existing approaches in challenging navigation tasks. The resulting reactive safe navigation (REASAN) system achieves fully onboard and real-time reactive navigation across both single- and multi-robot settings in complex environments. We release our training and deployment code at https://github.com/ASIG-X/REASAN.
RESPLE: Recursive Spline Estimation for LiDAR-Based Odometry
Apr 15, 2025Abstract:We present a novel recursive Bayesian estimation framework for continuous-time six-DoF dynamic motion estimation using B-splines. The state vector consists of a recurrent set of position control points and orientation control point increments, enabling a straightforward modification of the iterated extended Kalman filter without involving the error-state formulation. The resulting recursive spline estimator (RESPLE) provides a versatile, pragmatic and lightweight solution for motion estimation and is further exploited for direct LiDAR-based odometry, supporting integration of one or multiple LiDARs and an IMU. We conduct extensive real-world benchmarking based on public datasets and own experiments, covering aerial, wheeled, legged, and wearable platforms operating in indoor, urban, wild environments with diverse LiDARs. RESPLE-based solutions achieve superior estimation accuracy and robustness over corresponding state-of-the-art systems, while attaining real-time performance. Notably, our LiDAR-only variant outperforms existing LiDAR-inertial systems in scenarios without significant LiDAR degeneracy, and showing further improvements when additional LiDAR and inertial sensors are incorporated for more challenging conditions. We release the source code and own experimental datasets at https://github.com/ASIG-X/RESPLE .
IRIS: An Immersive Robot Interaction System
Feb 05, 2025



Abstract:This paper introduces IRIS, an immersive Robot Interaction System leveraging Extended Reality (XR), designed for robot data collection and interaction across multiple simulators, benchmarks, and real-world scenarios. While existing XR-based data collection systems provide efficient and intuitive solutions for large-scale data collection, they are often challenging to reproduce and reuse. This limitation arises because current systems are highly tailored to simulator-specific use cases and environments. IRIS is a novel, easily extendable framework that already supports multiple simulators, benchmarks, and even headsets. Furthermore, IRIS is able to include additional information from real-world sensors, such as point clouds captured through depth cameras. A unified scene specification is generated directly from simulators or real-world sensors and transmitted to XR headsets, creating identical scenes in XR. This specification allows IRIS to support any of the objects, assets, and robots provided by the simulators. In addition, IRIS introduces shared spatial anchors and a robust communication protocol that links simulations between multiple XR headsets. This feature enables multiple XR headsets to share a synchronized scene, facilitating collaborative and multi-user data collection. IRIS can be deployed on any device that supports the Unity Framework, encompassing the vast majority of commercially available headsets. In this work, IRIS was deployed and tested on the Meta Quest 3 and the HoloLens 2. IRIS showcased its versatility across a wide range of real-world and simulated scenarios, using current popular robot simulators such as MuJoCo, IsaacSim, CoppeliaSim, and Genesis. In addition, a user study evaluates IRIS on a data collection task for the LIBERO benchmark. The study shows that IRIS significantly outperforms the baseline in both objective and subjective metrics.
Solving Zero-Shot 3D Visual Grounding as Constraint Satisfaction Problems
Nov 21, 2024Abstract:3D visual grounding (3DVG) aims to locate objects in a 3D scene with natural language descriptions. Supervised methods have achieved decent accuracy, but have a closed vocabulary and limited language understanding ability. Zero-shot methods mostly utilize large language models (LLMs) to handle natural language descriptions, yet suffer from slow inference speed. To address these problems, in this work, we propose a zero-shot method that reformulates the 3DVG task as a Constraint Satisfaction Problem (CSP), where the variables and constraints represent objects and their spatial relations, respectively. This allows a global reasoning of all relevant objects, producing grounding results of both the target and anchor objects. Moreover, we demonstrate the flexibility of our framework by handling negation- and counting-based queries with only minor extra coding efforts. Our system, Constraint Satisfaction Visual Grounding (CSVG), has been extensively evaluated on the public datasets ScanRefer and Nr3D datasets using only open-source LLMs. Results show the effectiveness of CSVG and superior grounding accuracy over current state-of-the-art zero-shot 3DVG methods with improvements of $+7.0\%$ (Acc@0.5 score) and $+11.2\%$ on the ScanRefer and Nr3D datasets, respectively. The code of our system is publicly available at https://github.com/sunsleaf/CSVG.
GPTR: Gaussian Process Trajectory Representation for Continuous-Time Motion Estimation
Oct 31, 2024



Abstract:Continuous-time trajectory representation has gained significant popularity in recent years, as it offers an elegant formulation that allows the fusion of a larger number of sensors and sensing modalities, overcoming limitations of traditional discrete-time frameworks. To bolster the adoption of the continuous-time paradigm, we propose a so-called Gaussian Process Trajectory Representation (GPTR) framework for continuous-time motion estimation (CTME) tasks. Our approach stands out by employing a third-order random jerk model, featuring closed-form expressions for both rotational and translational state derivatives. This model provides smooth, continuous trajectory representations that are crucial for precise estimation of complex motion. To support the wider robotics and computer vision communities, we have made the source code for GPTR available as a light-weight header-only library. This format was chosen for its ease of integration, allowing developers to incorporate GPTR into existing systems without needing extensive code modifications. Moreover, we also provide a set of optimization examples with LiDAR, camera, IMU, UWB factors, and closed-form analytical Jacobians under the proposed GP framework. Our experiments demonstrate the efficacy and efficiency of GP-based trajectory representation in various motion estimation tasks, and the examples can serve as the prototype to help researchers quickly develop future applications such as batch optimization, calibration, sensor fusion, trajectory planning, etc., with continuous-time trajectory representation. Our project is accessible at https://github.com/brytsknguyen/gptr .
Joint State and Parameter Estimation Using the Partial Errors-in-Variables Principle
Jul 01, 2024

Abstract:This letter proposes a new method for joint state and parameter estimation in uncertain dynamical systems. We exploit the partial errors-in-variables (PEIV) principle and formulate a regression problem in the sense of weighted total least squares, where the uncertainty in the parameter prior is explicitly considered. Based thereon, the PEIV regression can be solved iteratively through the Kalman smoothing and the regularized least squares for estimating the state and the parameter, respectively. The simulations demonstrate improved accuracy of the proposed method compared to existing approaches, including the joint maximum a posterior-maximum likelihood, the expectation maximisation, and the augmented state extended Kalman smoother.
Gaussian Process on the Product of Directional Manifolds
Mar 13, 2023



Abstract:We present a principled study on establishing Gaussian processes over variables on the product of directional manifolds. As a basic functional component, a manifold-adaptive kernel is presented based on the von Mises distribution for Gaussian process regression on unit circles. Afterward, a novel hypertoroidal von Mises kernel is introduced to enable topology-aware Gaussian processes on hypertori with consideration of correlational circular components. Based thereon, we enable multi-output regression for learning vector-valued functions on hypertori using intrinsic coregionalization model and provide analytical derivatives in hyperparameter optimization. The proposed multi-output hypertoroidal Gaussian process is further embedded to a data-driven recursive estimation scheme for learning unknown range sensing models of angle-of-arrival inputs. Evaluations on range-based localization show that the proposed scheme enables superior tracking accuracy over parametric modeling and common Gaussian processes.
Continuous-Time Ultra-Wideband-Inertial Fusion
Jan 22, 2023Abstract:We present a novel continuous-time online state estimation framework using ultra-wideband and inertial sensors. For representing motion states continuously over time, quaternion-based cubic B-splines are exploited with efficient solutions to kinematic interpolations and spatial differentiations. Based thereon, a sliding-window spline fitting scheme is established for asynchronous multi-sensor fusion and online calibration. We evaluate the proposed system, SFUISE (spline fusion-based ultra-wideband-inertial state estimation), in real-world scenarios based on public data set and experiments. The proposed spline fusion scheme is real-time capable and delivers superior performance over state-of-the-art discrete-time schemes. We release the source code and own experimental data set at https://github.com/KIT-ISAS/SFUISE.
Towards High-Performance Solid-State-LiDAR-Inertial Odometry and Mapping
Oct 31, 2020
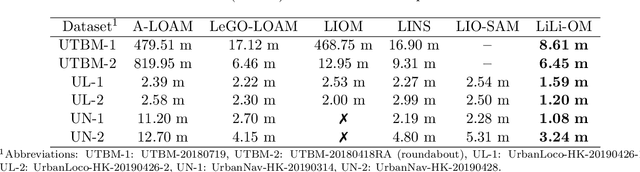
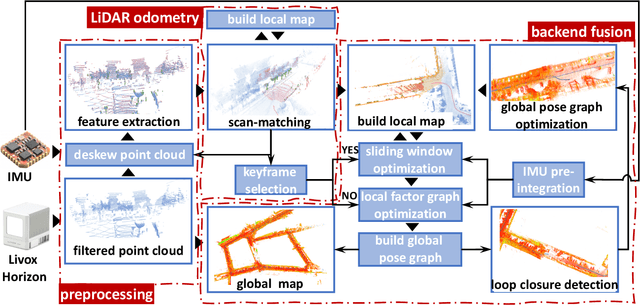

Abstract:We present a novel tightly-coupled LiDAR-inertial odometry and mapping scheme for both solid-state and mechanical LiDARs. As frontend, a feature-based lightweight LiDAR odometry provides fast motion estimates for adaptive keyframe selection. As backend, a hierarchical keyframe-based sliding window optimization is performed through marginalization for directly fusing IMU and LiDAR measurements. For the Livox Horizon, a newly released solid-state LiDAR, a novel feature extraction method is proposed to handle its irregular scan pattern during preprocessing. LiLi-OM (Livox LiDAR-inertial odometry and mapping) is real-time capable and achieves superior accuracy over state-of-the-art systems for both LiDAR types on public data sets of mechanical LiDARs and in experiments using the Livox Horizon. Source code and recorded experimental data sets are available on Github.
Improved Pose Graph Optimization for Planar Motions Using Riemannian Geometry on the Manifold of Dual Quaternions
Jul 31, 2019
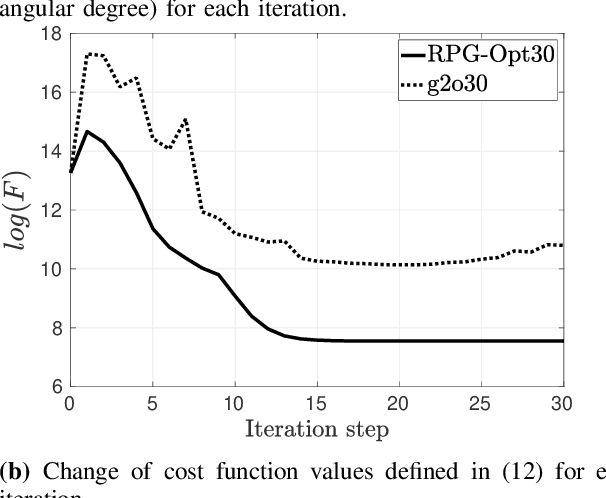
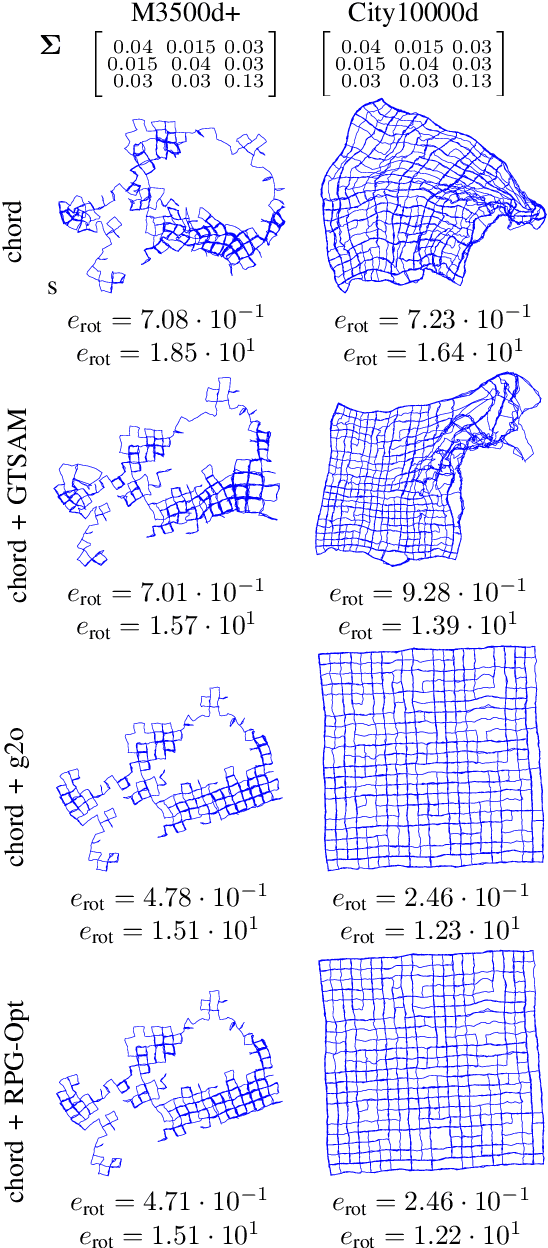

Abstract:We present a novel Riemannian approach for planar pose graph optimization problems. By formulating the cost function based on the Riemannian metric on the manifold of dual quaternions representing planar motions, the nonlinear structure of the SE(2) group is inherently considered. To solve the on-manifold least squares problem, a Riemannian Gauss-Newton method using the exponential retraction is applied. The proposed Riemannian pose graph optimizer (RPG-Opt) is further compared with currently popular optimization frameworks using public planar pose graph datasets. Evaluations show that the proposed method gives equivalently accurate results as the state-of-the-art frameworks and shows better convergence robustness under large uncertainties of odometry measurements.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge