Progressive Bayesian Particle Flows based on Optimal Transport Map Sequences

We propose a method for optimal Bayesian filtering with deterministic particles. In order to avoid particle degeneration, the filter step is not performed at once. Instead, the particles progressively flow from prior to posterior. This is achieved by splitting the filter step into a series of sub-steps. In each sub-step, optimal resampling is done by a map that replaces non-equally weighted particles with equally weighted ones. Inversions of the maps or monotonicity constraints are not required, greatly simplifying the procedure. The parameters of the mapping network are optimized w.r.t.\ to a particle set distance. This distance is differentiable, and compares non-equally and equally weighted particles. Composition of the map sequence provides a final mapping from prior to posterior particles. Radial basis function neural networks are used as maps. It is important that no intermediate continuous density representation is required. The entire flow works directly with particle representations. This avoids costly density estimation.

Continuous-Time Ultra-Wideband-Inertial Fusion

We present a novel continuous-time online state estimation framework using ultra-wideband and inertial sensors. For representing motion states continuously over time, quaternion-based cubic B-splines are exploited with efficient solutions to kinematic interpolations and spatial differentiations. Based thereon, a sliding-window spline fitting scheme is established for asynchronous multi-sensor fusion and online calibration. We evaluate the proposed system, SFUISE (spline fusion-based ultra-wideband-inertial state estimation), in real-world scenarios based on public data set and experiments. The proposed spline fusion scheme is real-time capable and delivers superior performance over state-of-the-art discrete-time schemes. We release the source code and own experimental data set at https://github.com/KIT-ISAS/SFUISE.

Gaussian Mixture Estimation from Weighted Samples

We consider estimating the parameters of a Gaussian mixture density with a given number of components best representing a given set of weighted samples. We adopt a density interpretation of the samples by viewing them as a discrete Dirac mixture density over a continuous domain with weighted components. Hence, Gaussian mixture fitting is viewed as density re-approximation. In order to speed up computation, an expectation-maximization method is proposed that properly considers not only the sample locations, but also the corresponding weights. It is shown that methods from literature do not treat the weights correctly, resulting in wrong estimates. This is demonstrated with simple counterexamples. The proposed method works in any number of dimensions with the same computational load as standard Gaussian mixture estimators for unweighted samples.

Three-dimensional Simultaneous Shape and Pose Estimation for Extended Objects Using Spherical Harmonics

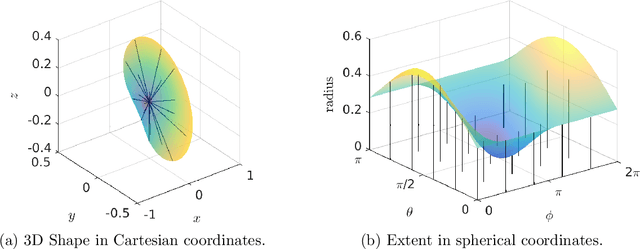
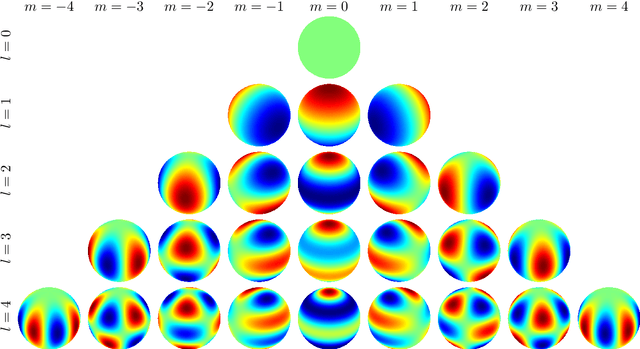
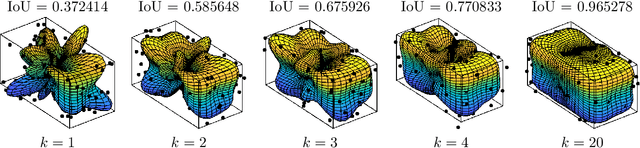
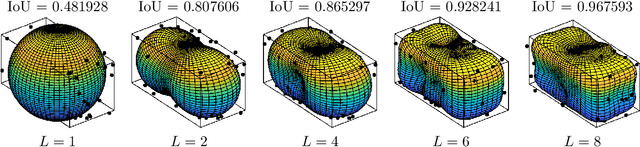
We propose a new recursive method for simultaneous estimation of both the pose and the shape of a three-dimensional extended object. The key idea of the presented method is to represent the shape of the object using spherical harmonics, similar to the way Fourier series can be used in the two-dimensional case. This allows us to derive a measurement equation that can be used within the framework of nonlinear filters such as the UKF. We provide both simulative and experimental evaluations of the novel techniques.

Towards High-Performance Solid-State-LiDAR-Inertial Odometry and Mapping

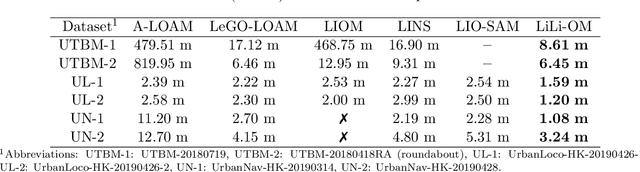
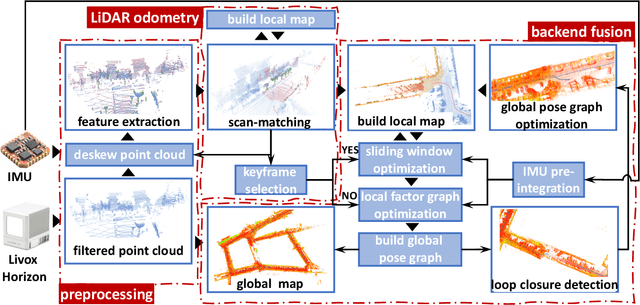
We present a novel tightly-coupled LiDAR-inertial odometry and mapping scheme for both solid-state and mechanical LiDARs. As frontend, a feature-based lightweight LiDAR odometry provides fast motion estimates for adaptive keyframe selection. As backend, a hierarchical keyframe-based sliding window optimization is performed through marginalization for directly fusing IMU and LiDAR measurements. For the Livox Horizon, a newly released solid-state LiDAR, a novel feature extraction method is proposed to handle its irregular scan pattern during preprocessing. LiLi-OM (Livox LiDAR-inertial odometry and mapping) is real-time capable and achieves superior accuracy over state-of-the-art systems for both LiDAR types on public data sets of mechanical LiDARs and in experiments using the Livox Horizon. Source code and recorded experimental data sets are available on Github.

iviz: A ROS Visualization App for Mobile Devices

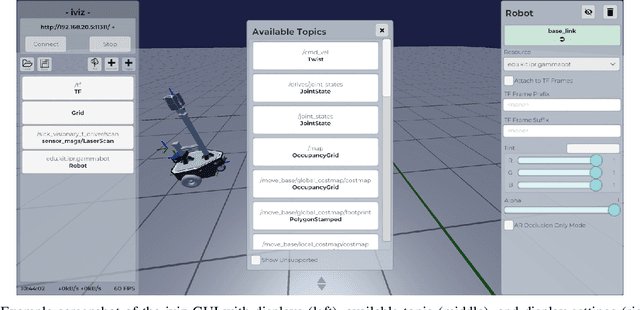
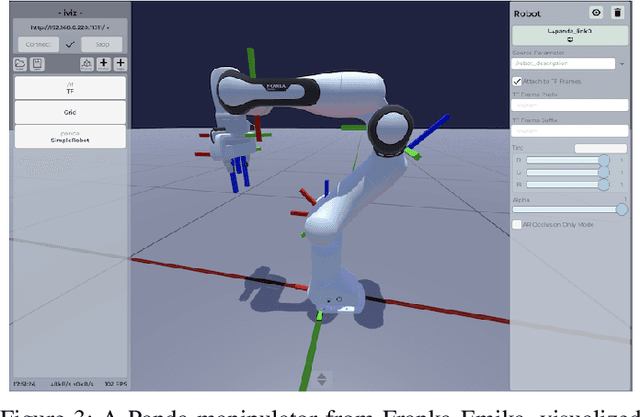
In this work, we introduce iviz, a mobile application for visualizing ROS data. In the last few years, the popularity of ROS has grown enormously, making it the standard platform for open source robotic programming. A key reason for this success is the availability of polished, general-purpose modules for many tasks, such as localization, mapping, path planning, and quite importantly, data visualization. However, the availability of the latter is generally restricted to PCs with the Linux operating system. Thus, users that want to see what is happening in the system with a smartphone or a tablet are stuck with solutions such as screen mirroring or using web browser versions of rviz, which are difficult to interact with from a mobile interface. More importantly, this makes newer visualization modalities such as Augmented Reality impossible. Our application iviz, based on the Unity engine, addresses these issues by providing a visualization platform designed from scratch to be usable in mobile platforms, such as iOS, Android, and UWP, and including native support for Augmented Reality for all three platforms. If desired, it can also be used in a PC with Linux, Windows, or macOS without any changes.

Improved Pose Graph Optimization for Planar Motions Using Riemannian Geometry on the Manifold of Dual Quaternions

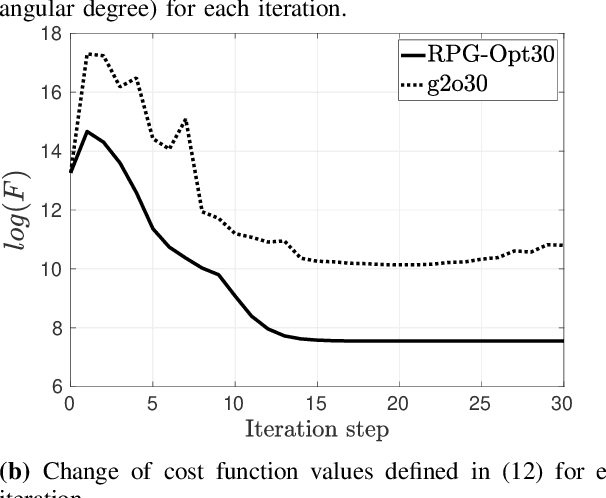
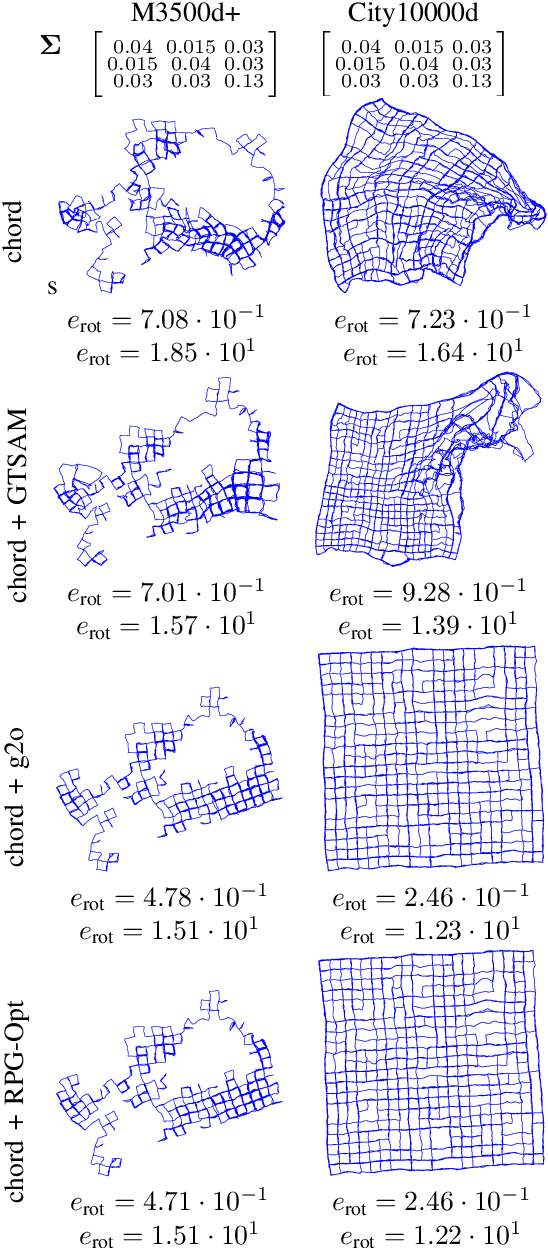
We present a novel Riemannian approach for planar pose graph optimization problems. By formulating the cost function based on the Riemannian metric on the manifold of dual quaternions representing planar motions, the nonlinear structure of the SE(2) group is inherently considered. To solve the on-manifold least squares problem, a Riemannian Gauss-Newton method using the exponential retraction is applied. The proposed Riemannian pose graph optimizer (RPG-Opt) is further compared with currently popular optimization frameworks using public planar pose graph datasets. Evaluations show that the proposed method gives equivalently accurate results as the state-of-the-art frameworks and shows better convergence robustness under large uncertainties of odometry measurements.

Directional Statistics and Filtering Using libDirectional

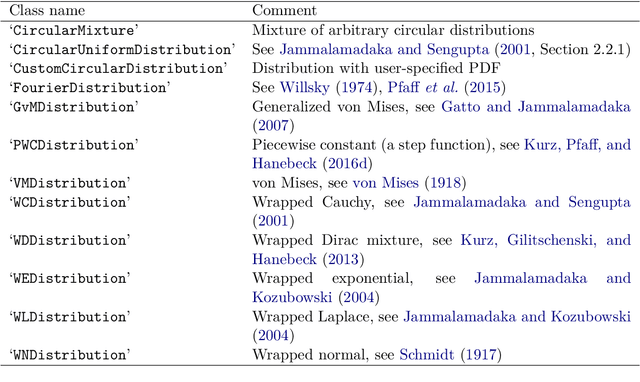
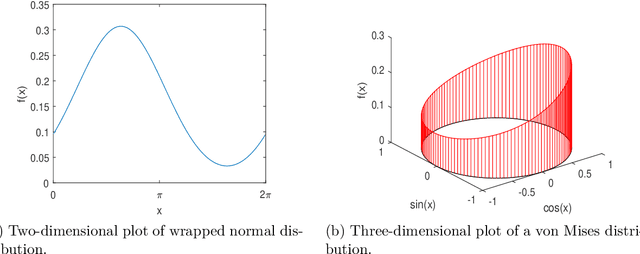
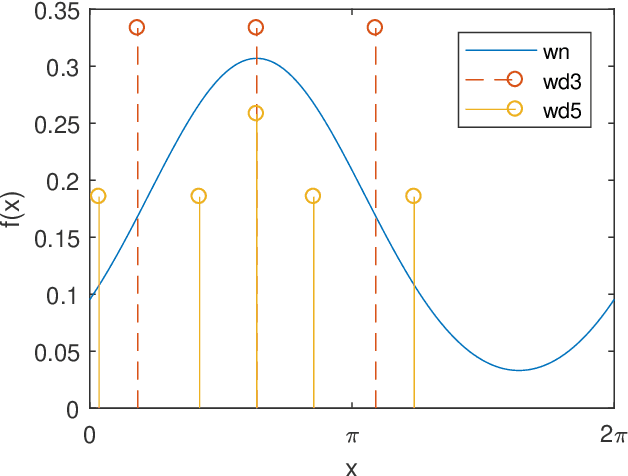
In this paper, we present libDirectional, a MATLAB library for directional statistics and directional estimation. It supports a variety of commonly used distributions on the unit circle, such as the von Mises, wrapped normal, and wrapped Cauchy distributions. Furthermore, various distributions on higher-dimensional manifolds such as the unit hypersphere and the hypertorus are available. Based on these distributions, several recursive filtering algorithms in libDirectional allow estimation on these manifolds. The functionality is implemented in a clear, well-documented, and object-oriented structure that is both easy to use and easy to extend.

Recursive Bayesian Filtering in Circular State Spaces

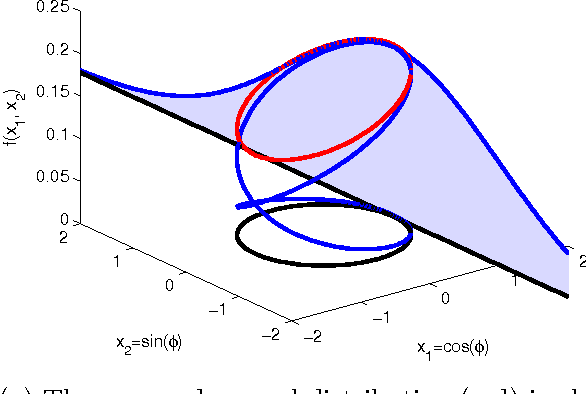
For recursive circular filtering based on circular statistics, we introduce a general framework for estimation of a circular state based on different circular distributions, specifically the wrapped normal distribution and the von Mises distribution. We propose an estimation method for circular systems with nonlinear system and measurement functions. This is achieved by relying on efficient deterministic sampling techniques. Furthermore, we show how the calculations can be simplified in a variety of important special cases, such as systems with additive noise as well as identity system or measurement functions. We introduce several novel key components, particularly a distribution-free prediction algorithm, a new and superior formula for the multiplication of wrapped normal densities, and the ability to deal with non-additive system noise. All proposed methods are thoroughly evaluated and compared to several state-of-the-art solutions.

Unscented Orientation Estimation Based on the Bingham Distribution

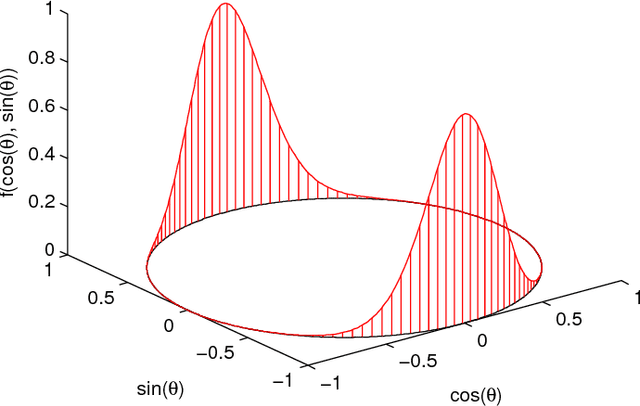
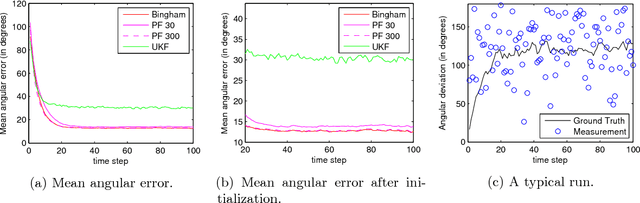
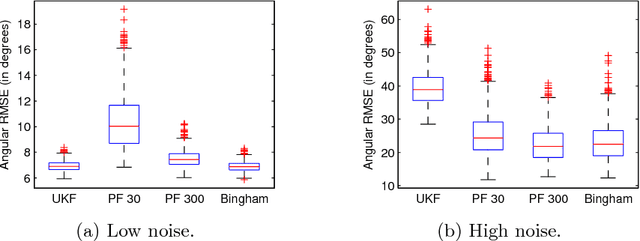
Orientation estimation for 3D objects is a common problem that is usually tackled with traditional nonlinear filtering techniques such as the extended Kalman filter (EKF) or the unscented Kalman filter (UKF). Most of these techniques assume Gaussian distributions to account for system noise and uncertain measurements. This distributional assumption does not consider the periodic nature of pose and orientation uncertainty. We propose a filter that considers the periodicity of the orientation estimation problem in its distributional assumption. This is achieved by making use of the Bingham distribution, which is defined on the hypersphere and thus inherently more suitable to periodic problems. Furthermore, handling of non-trivial system functions is done using deterministic sampling in an efficient way. A deterministic sampling scheme reminiscent of the UKF is proposed for the nonlinear manifold of orientations. It is the first deterministic sampling scheme that truly reflects the nonlinear manifold of the orientation.