Unscented Orientation Estimation Based on the Bingham Distribution
Paper and Code
Nov 22, 2013
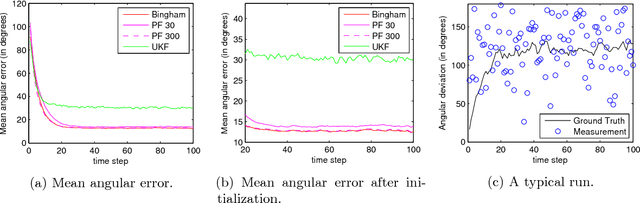
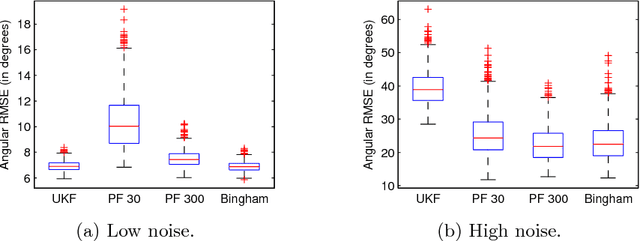
Orientation estimation for 3D objects is a common problem that is usually tackled with traditional nonlinear filtering techniques such as the extended Kalman filter (EKF) or the unscented Kalman filter (UKF). Most of these techniques assume Gaussian distributions to account for system noise and uncertain measurements. This distributional assumption does not consider the periodic nature of pose and orientation uncertainty. We propose a filter that considers the periodicity of the orientation estimation problem in its distributional assumption. This is achieved by making use of the Bingham distribution, which is defined on the hypersphere and thus inherently more suitable to periodic problems. Furthermore, handling of non-trivial system functions is done using deterministic sampling in an efficient way. A deterministic sampling scheme reminiscent of the UKF is proposed for the nonlinear manifold of orientations. It is the first deterministic sampling scheme that truly reflects the nonlinear manifold of the orientation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge