Improved Pose Graph Optimization for Planar Motions Using Riemannian Geometry on the Manifold of Dual Quaternions

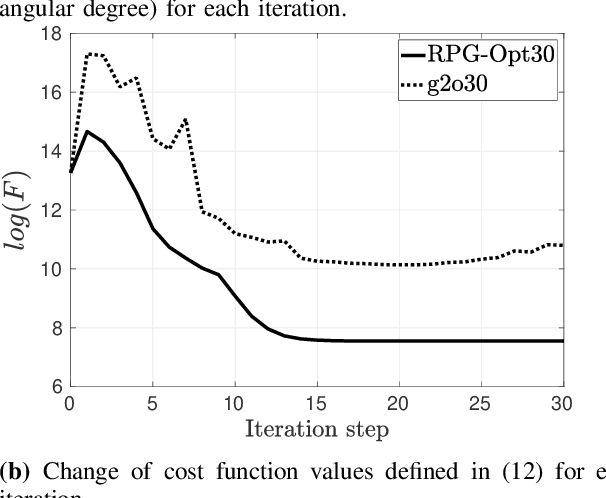
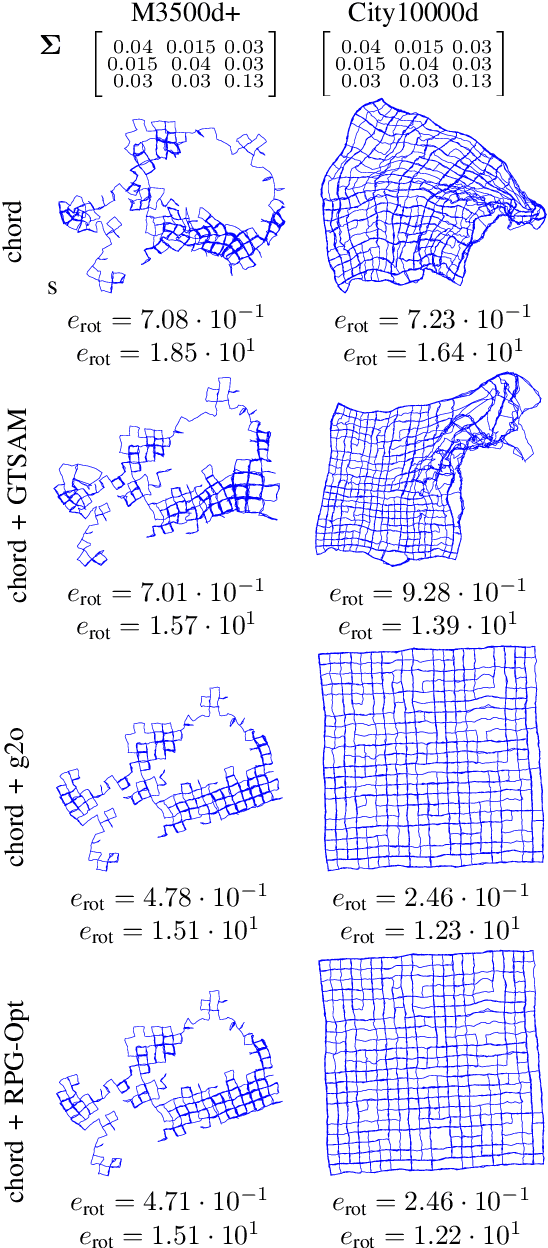
We present a novel Riemannian approach for planar pose graph optimization problems. By formulating the cost function based on the Riemannian metric on the manifold of dual quaternions representing planar motions, the nonlinear structure of the SE(2) group is inherently considered. To solve the on-manifold least squares problem, a Riemannian Gauss-Newton method using the exponential retraction is applied. The proposed Riemannian pose graph optimizer (RPG-Opt) is further compared with currently popular optimization frameworks using public planar pose graph datasets. Evaluations show that the proposed method gives equivalently accurate results as the state-of-the-art frameworks and shows better convergence robustness under large uncertainties of odometry measurements.