Safe Active Learning for Time-Series Modeling with Gaussian Processes

Learning time-series models is useful for many applications, such as simulation and forecasting. In this study, we consider the problem of actively learning time-series models while taking given safety constraints into account. For time-series modeling we employ a Gaussian process with a nonlinear exogenous input structure. The proposed approach generates data appropriate for time series model learning, i.e. input and output trajectories, by dynamically exploring the input space. The approach parametrizes the input trajectory as consecutive trajectory sections, which are determined stepwise given safety requirements and past observations. We analyze the proposed algorithm and evaluate it empirically on a technical application. The results show the effectiveness of our approach in a realistic technical use case.

Amortized Inference for Gaussian Process Hyperparameters of Structured Kernels

Learning the kernel parameters for Gaussian processes is often the computational bottleneck in applications such as online learning, Bayesian optimization, or active learning. Amortizing parameter inference over different datasets is a promising approach to dramatically speed up training time. However, existing methods restrict the amortized inference procedure to a fixed kernel structure. The amortization network must be redesigned manually and trained again in case a different kernel is employed, which leads to a large overhead in design time and training time. We propose amortizing kernel parameter inference over a complete kernel-structure-family rather than a fixed kernel structure. We do that via defining an amortization network over pairs of datasets and kernel structures. This enables fast kernel inference for each element in the kernel family without retraining the amortization network. As a by-product, our amortization network is able to do fast ensembling over kernel structures. In our experiments, we show drastically reduced inference time combined with competitive test performance for a large set of kernels and datasets.

Hierarchical-Hyperplane Kernels for Actively Learning Gaussian Process Models of Nonstationary Systems

Learning precise surrogate models of complex computer simulations and physical machines often require long-lasting or expensive experiments. Furthermore, the modeled physical dependencies exhibit nonlinear and nonstationary behavior. Machine learning methods that are used to produce the surrogate model should therefore address these problems by providing a scheme to keep the number of queries small, e.g. by using active learning and be able to capture the nonlinear and nonstationary properties of the system. One way of modeling the nonstationarity is to induce input-partitioning, a principle that has proven to be advantageous in active learning for Gaussian processes. However, these methods either assume a known partitioning, need to introduce complex sampling schemes or rely on very simple geometries. In this work, we present a simple, yet powerful kernel family that incorporates a partitioning that: i) is learnable via gradient-based methods, ii) uses a geometry that is more flexible than previous ones, while still being applicable in the low data regime. Thus, it provides a good prior for active learning procedures. We empirically demonstrate excellent performance on various active learning tasks.

Spatial Decompositions for Large Scale SVMs

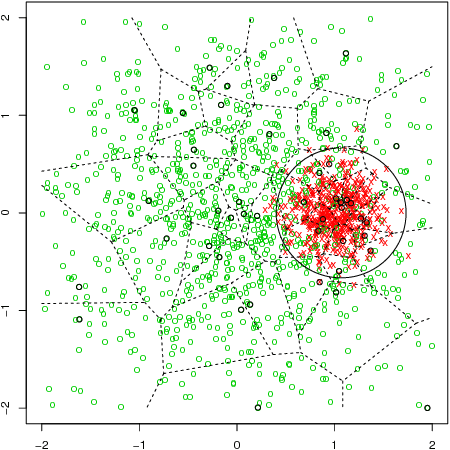
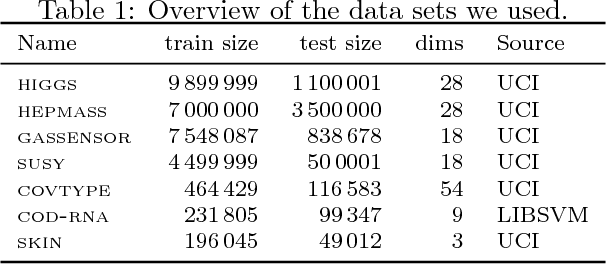
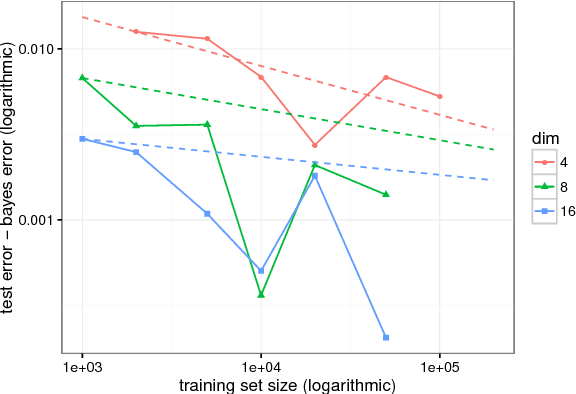
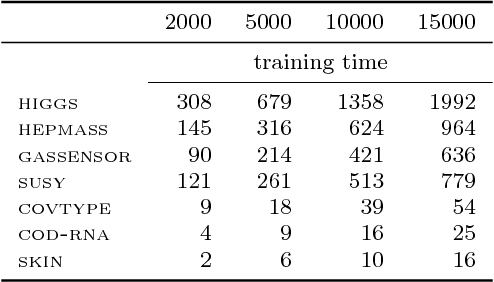
Although support vector machines (SVMs) are theoretically well understood, their underlying optimization problem becomes very expensive, if, for example, hundreds of thousands of samples and a non-linear kernel are considered. Several approaches have been proposed in the past to address this serious limitation. In this work we investigate a decomposition strategy that learns on small, spatially defined data chunks. Our contributions are two fold: On the theoretical side we establish an oracle inequality for the overall learning method using the hinge loss, and show that the resulting rates match those known for SVMs solving the complete optimization problem with Gaussian kernels. On the practical side we compare our approach to learning SVMs on small, randomly chosen chunks. Here it turns out that for comparable training times our approach is significantly faster during testing and also reduces the test error in most cases significantly. Furthermore, we show that our approach easily scales up to 10 million training samples: including hyper-parameter selection using cross validation, the entire training only takes a few hours on a single machine. Finally, we report an experiment on 32 million training samples. All experiments used liquidSVM (Steinwart and Thomann, 2017).