Better by Default: Strong Pre-Tuned MLPs and Boosted Trees on Tabular Data

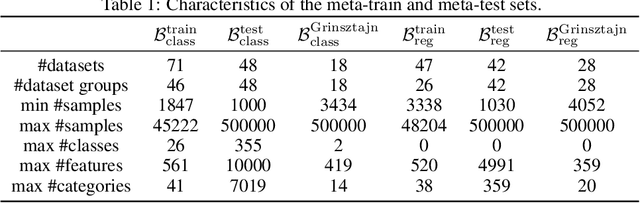
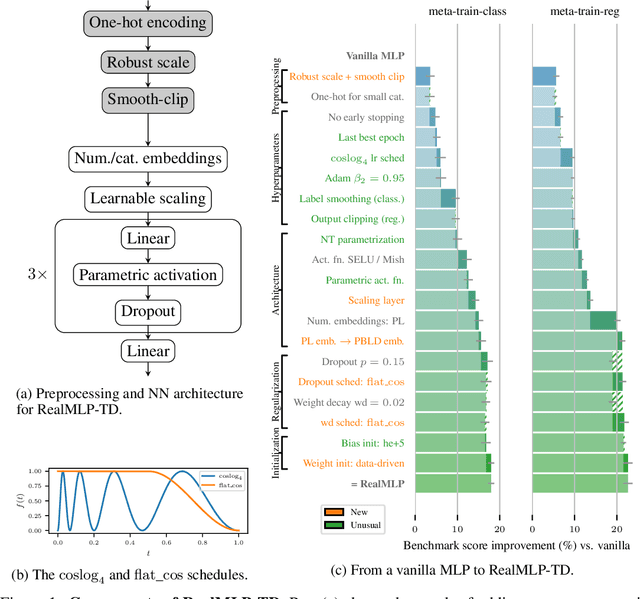
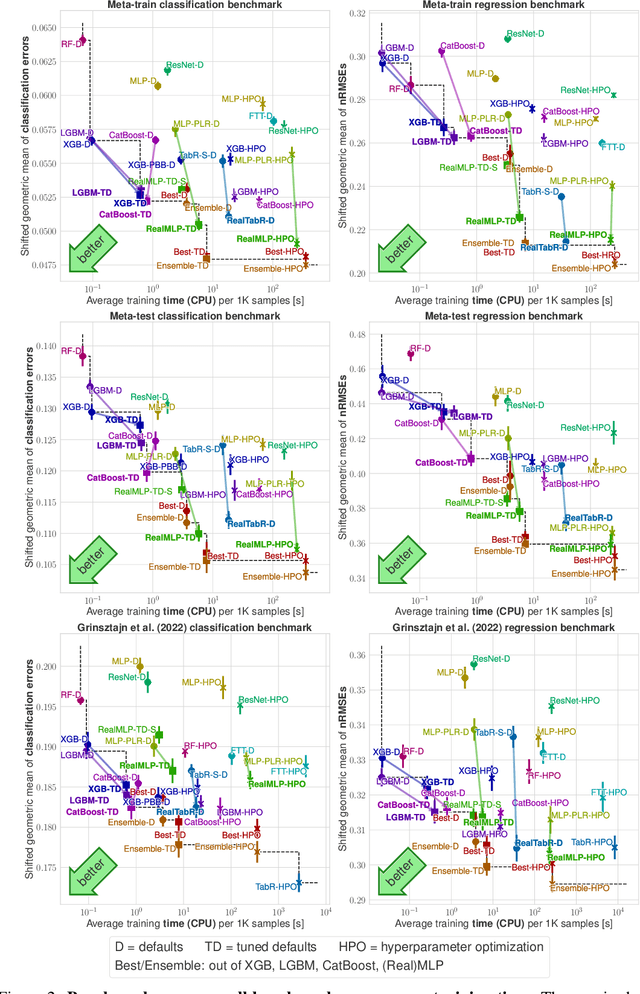
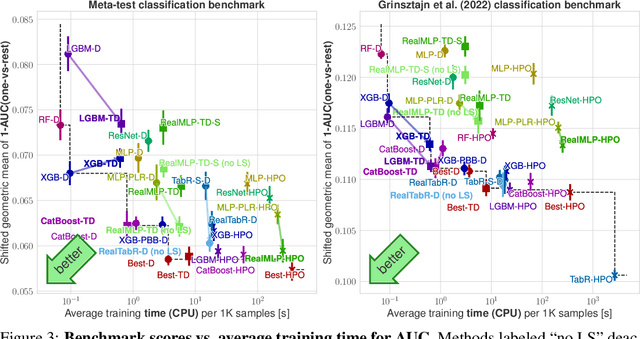
For classification and regression on tabular data, the dominance of gradient-boosted decision trees (GBDTs) has recently been challenged by often much slower deep learning methods with extensive hyperparameter tuning. We address this discrepancy by introducing (a) RealMLP, an improved multilayer perceptron (MLP), and (b) improved default parameters for GBDTs and RealMLP. We tune RealMLP and the default parameters on a meta-train benchmark with 71 classification and 47 regression datasets and compare them to hyperparameter-optimized versions on a disjoint meta-test benchmark with 48 classification and 42 regression datasets, as well as the GBDT-friendly benchmark by Grinsztajn et al. (2022). Our benchmark results show that RealMLP offers a better time-accuracy tradeoff than other neural nets and is competitive with GBDTs. Moreover, a combination of RealMLP and GBDTs with improved default parameters can achieve excellent results on medium-sized tabular datasets (1K--500K samples) without hyperparameter tuning.

Conditioning of Banach Space Valued Gaussian Random Variables: An Approximation Approach Based on Martingales

In this paper we investigate the conditional distributions of two Banach space valued, jointly Gaussian random variables. These conditional distributions are again Gaussian and their means and covariances are determined by a general approximation scheme based upon a martingale idea. We then apply our general results to the case of Gaussian processes with continuous paths conditioned to partial observations of their paths.

Mind the spikes: Benign overfitting of kernels and neural networks in fixed dimension

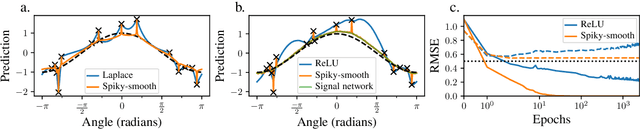
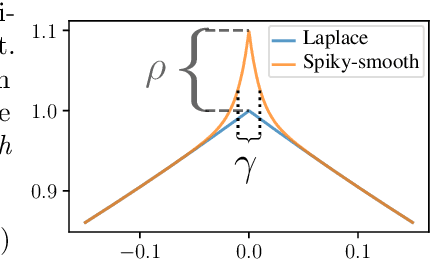
The success of over-parameterized neural networks trained to near-zero training error has caused great interest in the phenomenon of benign overfitting, where estimators are statistically consistent even though they interpolate noisy training data. While benign overfitting in fixed dimension has been established for some learning methods, current literature suggests that for regression with typical kernel methods and wide neural networks, benign overfitting requires a high-dimensional setting where the dimension grows with the sample size. In this paper, we show that the smoothness of the estimators, and not the dimension, is the key: benign overfitting is possible if and only if the estimator's derivatives are large enough. We generalize existing inconsistency results to non-interpolating models and more kernels to show that benign overfitting with moderate derivatives is impossible in fixed dimension. Conversely, we show that benign overfitting is possible for regression with a sequence of spiky-smooth kernels with large derivatives. Using neural tangent kernels, we translate our results to wide neural networks. We prove that while infinite-width networks do not overfit benignly with the ReLU activation, this can be fixed by adding small high-frequency fluctuations to the activation function. Our experiments verify that such neural networks, while overfitting, can indeed generalize well even on low-dimensional data sets.

Physics-Informed Gaussian Process Regression Generalizes Linear PDE Solvers

Linear partial differential equations (PDEs) are an important, widely applied class of mechanistic models, describing physical processes such as heat transfer, electromagnetism, and wave propagation. In practice, specialized numerical methods based on discretization are used to solve PDEs. They generally use an estimate of the unknown model parameters and, if available, physical measurements for initialization. Such solvers are often embedded into larger scientific models or analyses with a downstream application such that error quantification plays a key role. However, by entirely ignoring parameter and measurement uncertainty, classical PDE solvers may fail to produce consistent estimates of their inherent approximation error. In this work, we approach this problem in a principled fashion by interpreting solving linear PDEs as physics-informed Gaussian process (GP) regression. Our framework is based on a key generalization of a widely-applied theorem for conditioning GPs on a finite number of direct observations to observations made via an arbitrary bounded linear operator. Crucially, this probabilistic viewpoint allows to (1) quantify the inherent discretization error; (2) propagate uncertainty about the model parameters to the solution; and (3) condition on noisy measurements. Demonstrating the strength of this formulation, we prove that it strictly generalizes methods of weighted residuals, a central class of PDE solvers including collocation, finite volume, pseudospectral, and (generalized) Galerkin methods such as finite element and spectral methods. This class can thus be directly equipped with a structured error estimate and the capability to incorporate uncertain model parameters and observations. In summary, our results enable the seamless integration of mechanistic models as modular building blocks into probabilistic models.

Utilizing Expert Features for Contrastive Learning of Time-Series Representations

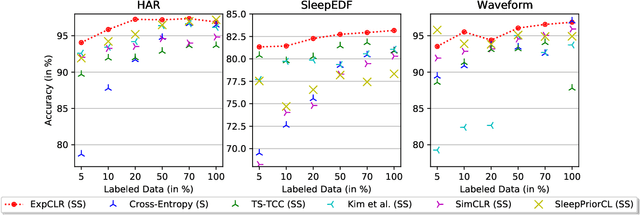
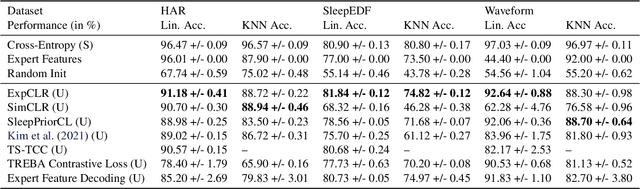
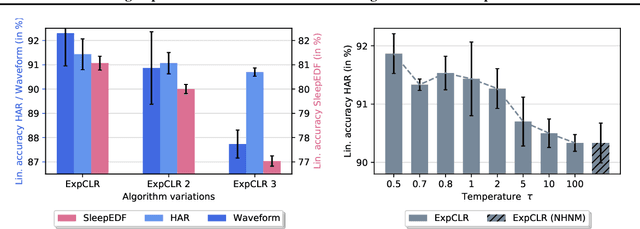
We present an approach that incorporates expert knowledge for time-series representation learning. Our method employs expert features to replace the commonly used data transformations in previous contrastive learning approaches. We do this since time-series data frequently stems from the industrial or medical field where expert features are often available from domain experts, while transformations are generally elusive for time-series data. We start by proposing two properties that useful time-series representations should fulfill and show that current representation learning approaches do not ensure these properties. We therefore devise ExpCLR, a novel contrastive learning approach built on an objective that utilizes expert features to encourage both properties for the learned representation. Finally, we demonstrate on three real-world time-series datasets that ExpCLR surpasses several state-of-the-art methods for both unsupervised and semi-supervised representation learning.

A Framework and Benchmark for Deep Batch Active Learning for Regression

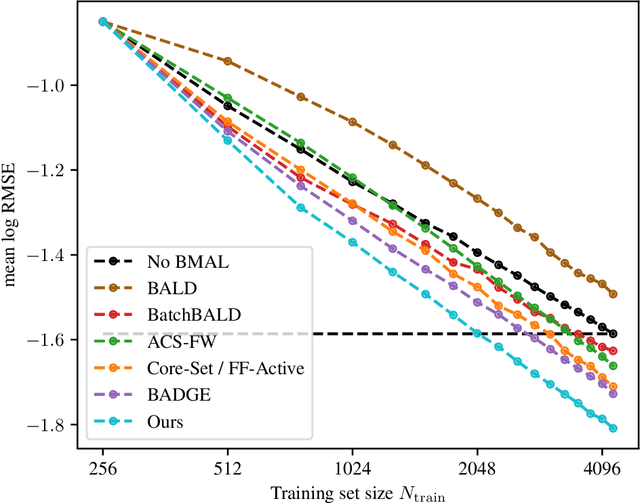
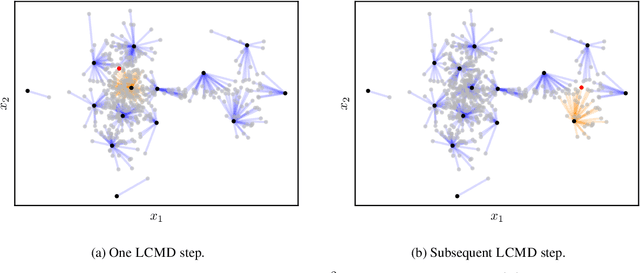
We study the performance of different pool-based Batch Mode Deep Active Learning (BMDAL) methods for regression on tabular data, focusing on methods that do not require to modify the network architecture and training. Our contributions are three-fold: First, we present a framework for constructing BMDAL methods out of kernels, kernel transformations and selection methods, showing that many of the most popular BMDAL methods fit into our framework. Second, we propose new components, leading to a new BMDAL method. Third, we introduce an open-source benchmark with 15 large tabular data sets, which we use to compare different BMDAL methods. Our benchmark results show that a combination of our novel components yields new state-of-the-art results in terms of RMSE and is computationally efficient. We provide open-source code that includes efficient implementations of all kernels, kernel transformations, and selection methods, and can be used for reproducing our results.

SOSP: Efficiently Capturing Global Correlations by Second-Order Structured Pruning

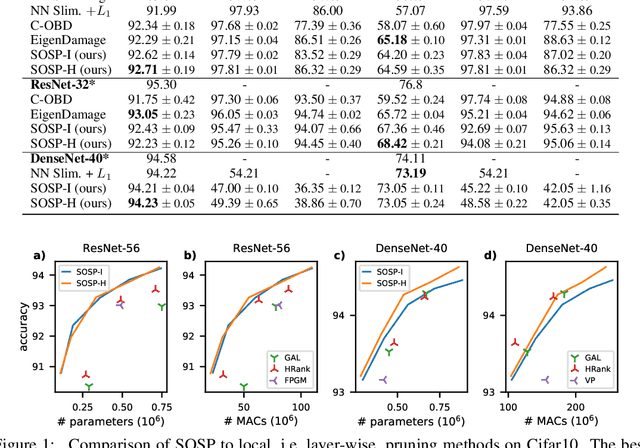
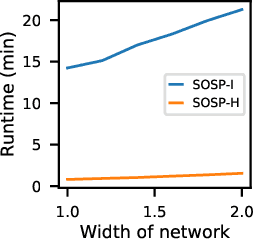
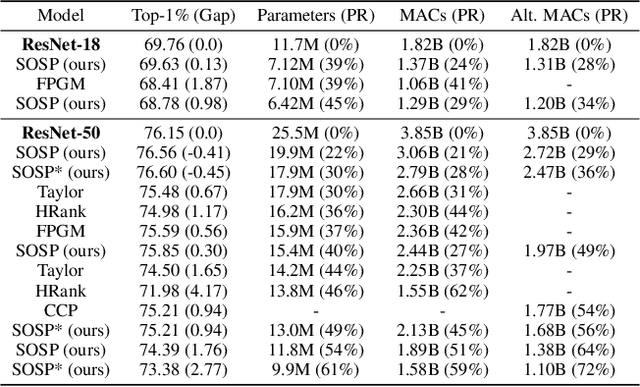
Pruning neural networks reduces inference time and memory costs. On standard hardware, these benefits will be especially prominent if coarse-grained structures, like feature maps, are pruned. We devise two novel saliency-based methods for second-order structured pruning (SOSP) which include correlations among all structures and layers. Our main method SOSP-H employs an innovative second-order approximation, which enables saliency evaluations by fast Hessian-vector products. SOSP-H thereby scales like a first-order method despite taking into account the full Hessian. We validate SOSP-H by comparing it to our second method SOSP-I that uses a well-established Hessian approximation, and to numerous state-of-the-art methods. While SOSP-H performs on par or better in terms of accuracy, it has clear advantages in terms of scalability and efficiency. This allowed us to scale SOSP-H to large-scale vision tasks, even though it captures correlations across all layers of the network. To underscore the global nature of our pruning methods, we evaluate their performance not only by removing structures from a pretrained network, but also by detecting architectural bottlenecks. We show that our algorithms allow to systematically reveal architectural bottlenecks, which we then remove to further increase the accuracy of the networks.

Fast and Sample-Efficient Interatomic Neural Network Potentials for Molecules and Materials Based on Gaussian Moments

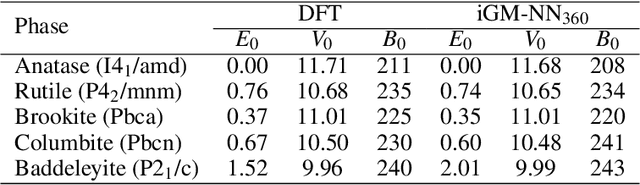
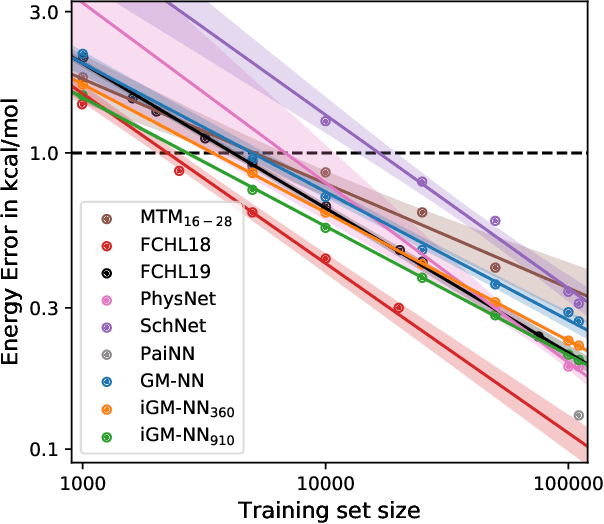
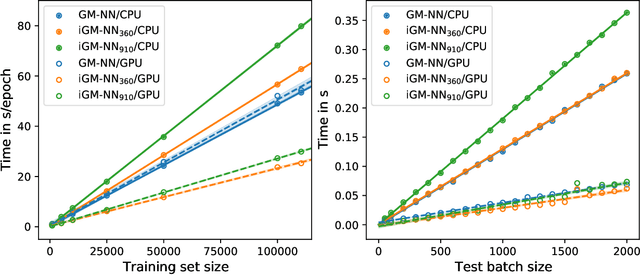
Artificial neural networks (NNs) are one of the most frequently used machine learning approaches to construct interatomic potentials and enable efficient large-scale atomistic simulations with almost ab initio accuracy. However, the simultaneous training of NNs on energies and forces, which are a prerequisite for, e.g., molecular dynamics simulations, can be demanding. In this work, we present an improved NN architecture based on the previous GM-NN model [V. Zaverkin and J. K\"astner, J. Chem. Theory Comput. 16, 5410-5421 (2020)], which shows an improved prediction accuracy and considerably reduced training times. Moreover, we extend the applicability of Gaussian moment-based interatomic potentials to periodic systems and demonstrate the overall excellent transferability and robustness of the respective models. The fast training by the improved methodology is a pre-requisite for training-heavy workflows such as active learning or learning-on-the-fly.

Which Minimizer Does My Neural Network Converge To?

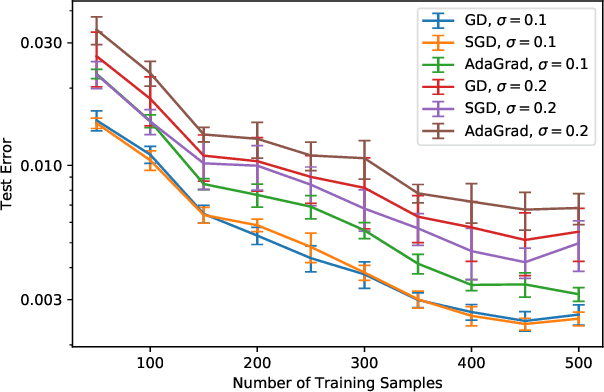
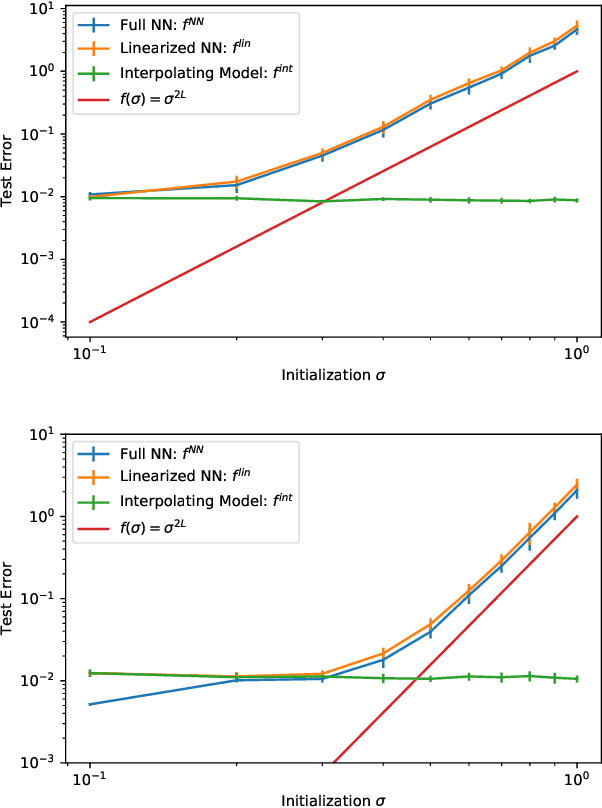
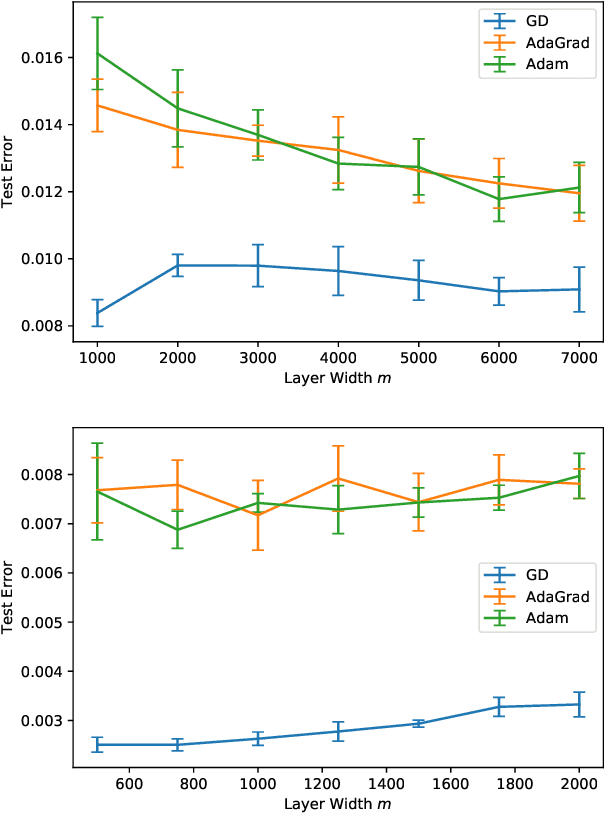
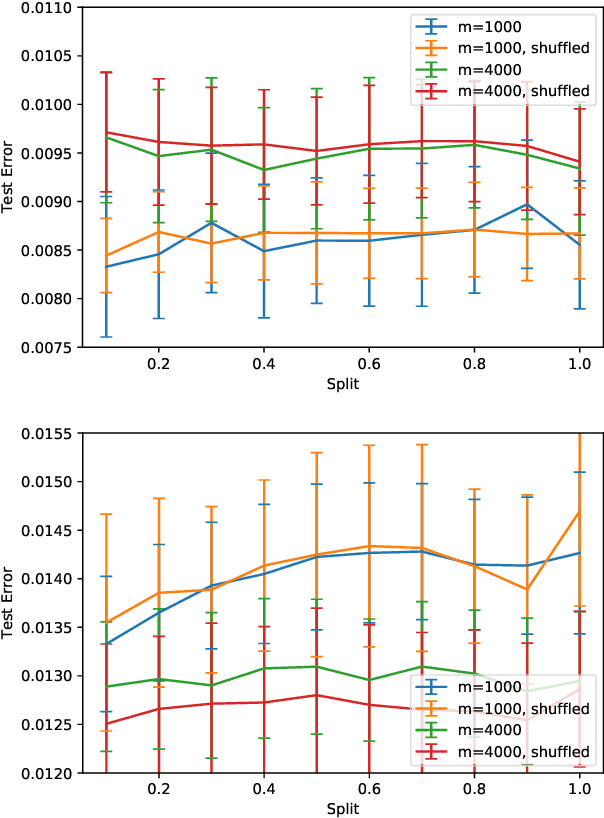
The loss surface of an overparameterized neural network (NN) possesses many global minima of zero training error. We explain how common variants of the standard NN training procedure change the minimizer obtained. First, we make explicit how the size of the initialization of a strongly overparameterized NN affects the minimizer and can deteriorate its final test performance. We propose a strategy to limit this effect. Then, we demonstrate that for adaptive optimization such as AdaGrad, the obtained minimizer generally differs from the gradient descent (GD) minimizer. This adaptive minimizer is changed further by stochastic mini-batch training, even though in the non-adaptive case GD and stochastic GD result in essentially the same minimizer. Lastly, we explain that these effects remain relevant for less overparameterized NNs. While overparameterization has its benefits, our work highlights that it induces sources of error absent from underparameterized models, some of which can be challenging to control.

Reproducing Kernel Hilbert Spaces Cannot Contain all Continuous Functions on a Compact Metric Space

Given an uncountable, compact metric space, we show that there exists no reproducing kernel Hilbert space that contains the space of all continuous functions on this compact space.