David Holzmüller
Conditional Coverage Diagnostics for Conformal Prediction
Dec 12, 2025Abstract:Evaluating conditional coverage remains one of the most persistent challenges in assessing the reliability of predictive systems. Although conformal methods can give guarantees on marginal coverage, no method can guarantee to produce sets with correct conditional coverage, leaving practitioners without a clear way to interpret local deviations. To overcome sample-inefficiency and overfitting issues of existing metrics, we cast conditional coverage estimation as a classification problem. Conditional coverage is violated if and only if any classifier can achieve lower risk than the target coverage. Through the choice of a (proper) loss function, the resulting risk difference gives a conservative estimate of natural miscoverage measures such as L1 and L2 distance, and can even separate the effects of over- and under-coverage, and non-constant target coverages. We call the resulting family of metrics excess risk of the target coverage (ERT). We show experimentally that the use of modern classifiers provides much higher statistical power than simple classifiers underlying established metrics like CovGap. Additionally, we use our metric to benchmark different conformal prediction methods. Finally, we release an open-source package for ERT as well as previous conditional coverage metrics. Together, these contributions provide a new lens for understanding, diagnosing, and improving the conditional reliability of predictive systems.
Structured Matrix Scaling for Multi-Class Calibration
Nov 05, 2025Abstract:Post-hoc recalibration methods are widely used to ensure that classifiers provide faithful probability estimates. We argue that parametric recalibration functions based on logistic regression can be motivated from a simple theoretical setting for both binary and multiclass classification. This insight motivates the use of more expressive calibration methods beyond standard temperature scaling. For multi-class calibration however, a key challenge lies in the increasing number of parameters introduced by more complex models, often coupled with limited calibration data, which can lead to overfitting. Through extensive experiments, we demonstrate that the resulting bias-variance tradeoff can be effectively managed by structured regularization, robust preprocessing and efficient optimization. The resulting methods lead to substantial gains over existing logistic-based calibration techniques. We provide efficient and easy-to-use open-source implementations of our methods, making them an attractive alternative to common temperature, vector, and matrix scaling implementations.
LOGLO-FNO: Efficient Learning of Local and Global Features in Fourier Neural Operators
Apr 05, 2025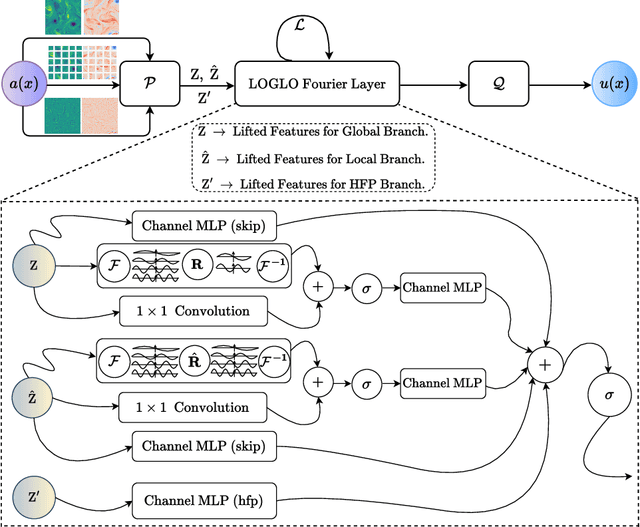
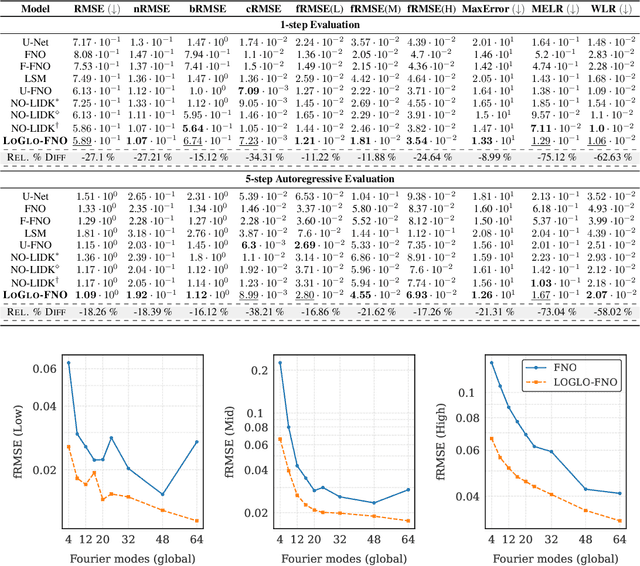

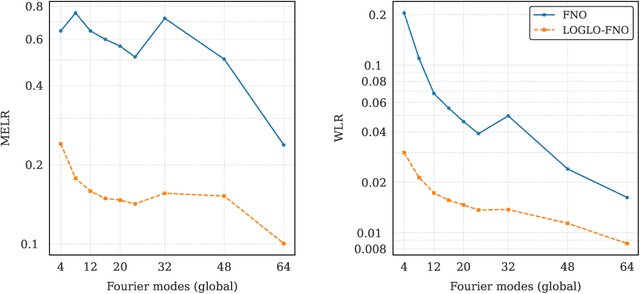
Abstract:Modeling high-frequency information is a critical challenge in scientific machine learning. For instance, fully turbulent flow simulations of Navier-Stokes equations at Reynolds numbers 3500 and above can generate high-frequency signals due to swirling fluid motions caused by eddies and vortices. Faithfully modeling such signals using neural networks depends on accurately reconstructing moderate to high frequencies. However, it has been well known that deep neural nets exhibit the so-called spectral bias toward learning low-frequency components. Meanwhile, Fourier Neural Operators (FNOs) have emerged as a popular class of data-driven models in recent years for solving Partial Differential Equations (PDEs) and for surrogate modeling in general. Although impressive results have been achieved on several PDE benchmark problems, FNOs often perform poorly in learning non-dominant frequencies characterized by local features. This limitation stems from the spectral bias inherent in neural networks and the explicit exclusion of high-frequency modes in FNOs and their variants. Therefore, to mitigate these issues and improve FNO's spectral learning capabilities to represent a broad range of frequency components, we propose two key architectural enhancements: (i) a parallel branch performing local spectral convolutions (ii) a high-frequency propagation module. Moreover, we propose a novel frequency-sensitive loss term based on radially binned spectral errors. This introduction of a parallel branch for local convolutions reduces number of trainable parameters by up to 50% while achieving the accuracy of baseline FNO that relies solely on global convolutions. Experiments on three challenging PDE problems in fluid mechanics and biological pattern formation, and the qualitative and spectral analysis of predictions show the effectiveness of our method over the state-of-the-art neural operator baselines.
TabICL: A Tabular Foundation Model for In-Context Learning on Large Data
Feb 08, 2025



Abstract:The long-standing dominance of gradient-boosted decision trees on tabular data is currently challenged by tabular foundation models using In-Context Learning (ICL): setting the training data as context for the test data and predicting in a single forward pass without parameter updates. While the very recent TabPFNv2 foundation model (2025) excels on tables with up to 10K samples, its alternating column- and row-wise attentions make handling large training sets computationally prohibitive. So, can ICL be effectively scaled and deliver a benefit for larger tables? We introduce TabICL, a tabular foundation model for classification, pretrained on synthetic datasets with up to 60K samples and capable of handling 500K samples on affordable resources. This is enabled by a novel two-stage architecture: a column-then-row attention mechanism to build fixed-dimensional embeddings of rows, followed by a transformer for efficient ICL. Across 200 classification datasets from the TALENT benchmark, TabICL is on par with TabPFNv2 while being systematically faster (up to 10 times), and significantly outperforms all other approaches. On 56 datasets with over 10K samples, TabICL surpasses both TabPFNv2 and CatBoost, demonstrating the potential of ICL for large data.
Rethinking Early Stopping: Refine, Then Calibrate
Jan 31, 2025Abstract:Machine learning classifiers often produce probabilistic predictions that are critical for accurate and interpretable decision-making in various domains. The quality of these predictions is generally evaluated with proper losses like cross-entropy, which decompose into two components: calibration error assesses general under/overconfidence, while refinement error measures the ability to distinguish different classes. In this paper, we provide theoretical and empirical evidence that these two errors are not minimized simultaneously during training. Selecting the best training epoch based on validation loss thus leads to a compromise point that is suboptimal for both calibration error and, most importantly, refinement error. To address this, we introduce a new metric for early stopping and hyperparameter tuning that makes it possible to minimize refinement error during training. The calibration error is minimized after training, using standard techniques. Our method integrates seamlessly with any architecture and consistently improves performance across diverse classification tasks.
Active Learning for Neural PDE Solvers
Aug 02, 2024


Abstract:Solving partial differential equations (PDEs) is a fundamental problem in engineering and science. While neural PDE solvers can be more efficient than established numerical solvers, they often require large amounts of training data that is costly to obtain. Active Learning (AL) could help surrogate models reach the same accuracy with smaller training sets by querying classical solvers with more informative initial conditions and PDE parameters. While AL is more common in other domains, it has yet to be studied extensively for neural PDE solvers. To bridge this gap, we introduce AL4PDE, a modular and extensible active learning benchmark. It provides multiple parametric PDEs and state-of-the-art surrogate models for the solver-in-the-loop setting, enabling the evaluation of existing and the development of new AL methods for PDE solving. We use the benchmark to evaluate batch active learning algorithms such as uncertainty- and feature-based methods. We show that AL reduces the average error by up to 71% compared to random sampling and significantly reduces worst-case errors. Moreover, AL generates similar datasets across repeated runs, with consistent distributions over the PDE parameters and initial conditions. The acquired datasets are reusable, providing benefits for surrogate models not involved in the data generation.
Better by Default: Strong Pre-Tuned MLPs and Boosted Trees on Tabular Data
Jul 05, 2024
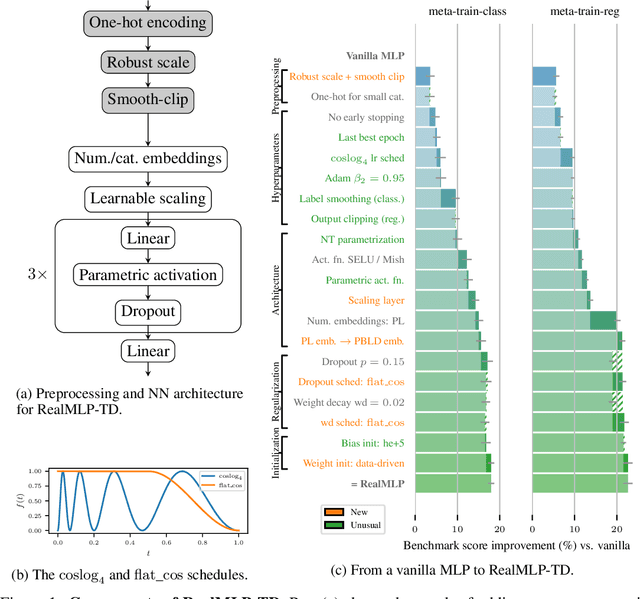
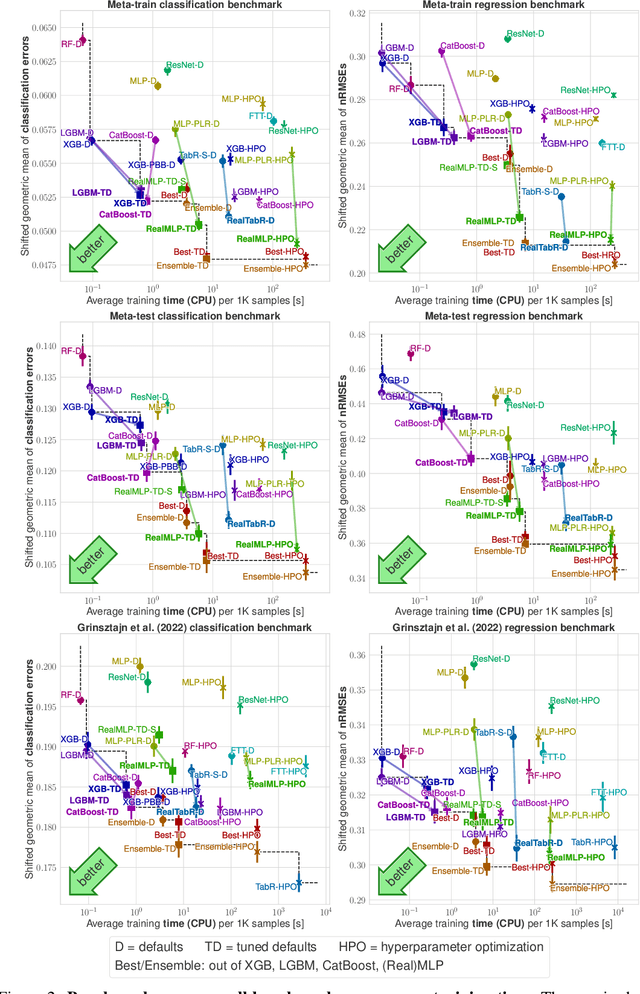
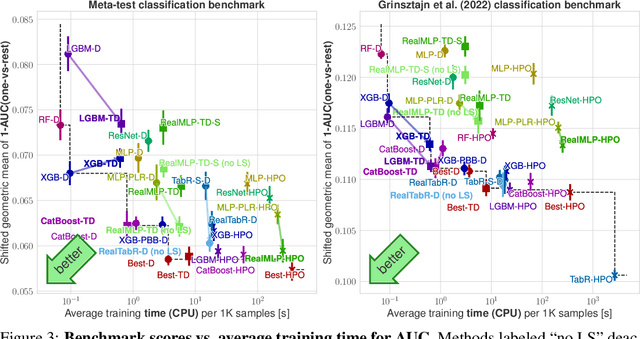
Abstract:For classification and regression on tabular data, the dominance of gradient-boosted decision trees (GBDTs) has recently been challenged by often much slower deep learning methods with extensive hyperparameter tuning. We address this discrepancy by introducing (a) RealMLP, an improved multilayer perceptron (MLP), and (b) improved default parameters for GBDTs and RealMLP. We tune RealMLP and the default parameters on a meta-train benchmark with 71 classification and 47 regression datasets and compare them to hyperparameter-optimized versions on a disjoint meta-test benchmark with 48 classification and 42 regression datasets, as well as the GBDT-friendly benchmark by Grinsztajn et al. (2022). Our benchmark results show that RealMLP offers a better time-accuracy tradeoff than other neural nets and is competitive with GBDTs. Moreover, a combination of RealMLP and GBDTs with improved default parameters can achieve excellent results on medium-sized tabular datasets (1K--500K samples) without hyperparameter tuning.
Predicting Properties of Periodic Systems from Cluster Data: A Case Study of Liquid Water
Dec 03, 2023Abstract:The accuracy of the training data limits the accuracy of bulk properties from machine-learned potentials. For example, hybrid functionals or wave-function-based quantum chemical methods are readily available for cluster data but effectively out-of-scope for periodic structures. We show that local, atom-centred descriptors for machine-learned potentials enable the prediction of bulk properties from cluster model training data, agreeing reasonably well with predictions from bulk training data. We demonstrate such transferability by studying structural and dynamical properties of bulk liquid water with density functional theory and have found an excellent agreement with experimental as well as theoretical counterparts.
Uncertainty-biased molecular dynamics for learning uniformly accurate interatomic potentials
Dec 03, 2023Abstract:Efficiently creating a concise but comprehensive data set for training machine-learned interatomic potentials (MLIPs) is an under-explored problem. Active learning (AL), which uses either biased or unbiased molecular dynamics (MD) simulations to generate candidate pools, aims to address this objective. Existing biased and unbiased MD simulations, however, are prone to miss either rare events or extrapolative regions -- areas of the configurational space where unreliable predictions are made. Simultaneously exploring both regions is necessary for developing uniformly accurate MLIPs. In this work, we demonstrate that MD simulations, when biased by the MLIP's energy uncertainty, effectively capture extrapolative regions and rare events without the need to know \textit{a priori} the system's transition temperatures and pressures. Exploiting automatic differentiation, we enhance bias-forces-driven MD simulations by introducing the concept of bias stress. We also employ calibrated ensemble-free uncertainties derived from sketched gradient features to yield MLIPs with similar or better accuracy than ensemble-based uncertainty methods at a lower computational cost. We use the proposed uncertainty-driven AL approach to develop MLIPs for two benchmark systems: alanine dipeptide and MIL-53(Al). Compared to MLIPs trained with conventional MD simulations, MLIPs trained with the proposed data-generation method more accurately represent the relevant configurational space for both atomic systems.
Mind the spikes: Benign overfitting of kernels and neural networks in fixed dimension
May 23, 2023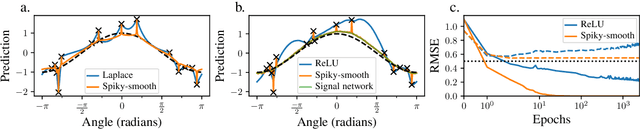
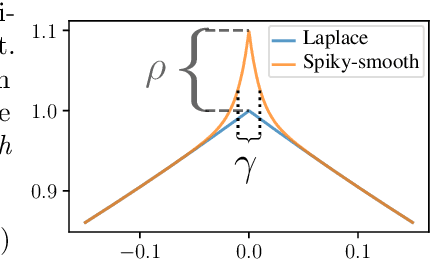

Abstract:The success of over-parameterized neural networks trained to near-zero training error has caused great interest in the phenomenon of benign overfitting, where estimators are statistically consistent even though they interpolate noisy training data. While benign overfitting in fixed dimension has been established for some learning methods, current literature suggests that for regression with typical kernel methods and wide neural networks, benign overfitting requires a high-dimensional setting where the dimension grows with the sample size. In this paper, we show that the smoothness of the estimators, and not the dimension, is the key: benign overfitting is possible if and only if the estimator's derivatives are large enough. We generalize existing inconsistency results to non-interpolating models and more kernels to show that benign overfitting with moderate derivatives is impossible in fixed dimension. Conversely, we show that benign overfitting is possible for regression with a sequence of spiky-smooth kernels with large derivatives. Using neural tangent kernels, we translate our results to wide neural networks. We prove that while infinite-width networks do not overfit benignly with the ReLU activation, this can be fixed by adding small high-frequency fluctuations to the activation function. Our experiments verify that such neural networks, while overfitting, can indeed generalize well even on low-dimensional data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge