Variational Kolmogorov-Arnold Network

Kolmogorov Arnold Networks (KANs) are an emerging architecture for building machine learning models. KANs are based on the theoretical foundation of the Kolmogorov-Arnold Theorem and its expansions, which provide an exact representation of a multi-variate continuous bounded function as the composition of a limited number of univariate continuous functions. While such theoretical results are powerful, their use as a representation learning alternative to a multi-layer perceptron (MLP) hinges on the ad-hoc choice of the number of bases modeling each of the univariate functions. In this work, we show how to address this problem by adaptively learning a potentially infinite number of bases for each univariate function during training. We therefore model the problem as a variational inference optimization problem. Our proposal, called InfinityKAN, which uses backpropagation, extends the potential applicability of KANs by treating an important hyperparameter as part of the learning process.

Oversmoothing, "Oversquashing", Heterophily, Long-Range, and more: Demystifying Common Beliefs in Graph Machine Learning

After a renaissance phase in which researchers revisited the message-passing paradigm through the lens of deep learning, the graph machine learning community shifted its attention towards a deeper and practical understanding of message-passing's benefits and limitations. In this position paper, we notice how the fast pace of progress around the topics of oversmoothing and oversquashing, the homophily-heterophily dichotomy, and long-range tasks, came with the consolidation of commonly accepted beliefs and assumptions that are not always true nor easy to distinguish from each other. We argue that this has led to ambiguities around the investigated problems, preventing researchers from focusing on and addressing precise research questions while causing a good amount of misunderstandings. Our contribution wants to make such common beliefs explicit and encourage critical thinking around these topics, supported by simple but noteworthy counterexamples. The hope is to clarify the distinction between the different issues and promote separate but intertwined research directions to address them.

Fast, Modular, and Differentiable Framework for Machine Learning-Enhanced Molecular Simulations

We present an end-to-end differentiable molecular simulation framework (DIMOS) for molecular dynamics and Monte Carlo simulations. DIMOS easily integrates machine-learning-based interatomic potentials and implements classical force fields including particle-mesh Ewald electrostatics. Thanks to its modularity, both classical and machine-learning-based approaches can be easily combined into a hybrid description of the system (ML/MM). By supporting key molecular dynamics features such as efficient neighborlists and constraint algorithms for larger time steps, the framework bridges the gap between hand-optimized simulation engines and the flexibility of a PyTorch implementation. The superior performance and the high versatility is probed in different benchmarks and applications, with speed-up factors of up to $170\times$. The advantage of differentiability is demonstrated by an end-to-end optimization of the proposal distribution in a Markov Chain Monte Carlo simulation based on Hamiltonian Monte Carlo. Using these optimized simulation parameters a $3\times$ acceleration is observed in comparison to ad-hoc chosen simulation parameters. The code is available at https://github.com/nec-research/DIMOS.

Adaptive Width Neural Networks

For almost 70 years, researchers have mostly relied on hyper-parameter tuning to pick the width of neural networks' layers out of many possible choices. This paper challenges the status quo by introducing an easy-to-use technique to learn an unbounded width of a neural network's layer during training. The technique does not rely on alternate optimization nor hand-crafted gradient heuristics; rather, it jointly optimizes the width and the parameters of each layer via simple backpropagation. We apply the technique to a broad range of data domains such as tables, images, texts, and graphs, showing how the width adapts to the task's difficulty. By imposing a soft ordering of importance among neurons, it is possible to truncate the trained network at virtually zero cost, achieving a smooth trade-off between performance and compute resources in a structured way. Alternatively, one can dynamically compress the network with no performance degradation. In light of recent foundation models trained on large datasets, believed to require billions of parameters and where hyper-parameter tuning is unfeasible due to huge training costs, our approach stands as a viable alternative for width learning.

What Did I Do Wrong? Quantifying LLMs' Sensitivity and Consistency to Prompt Engineering

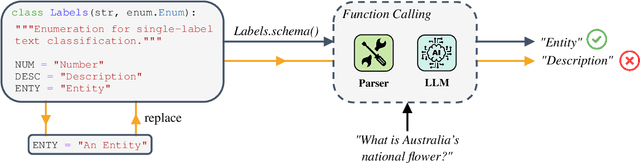
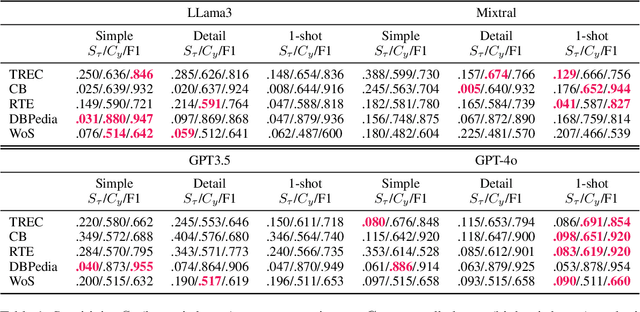
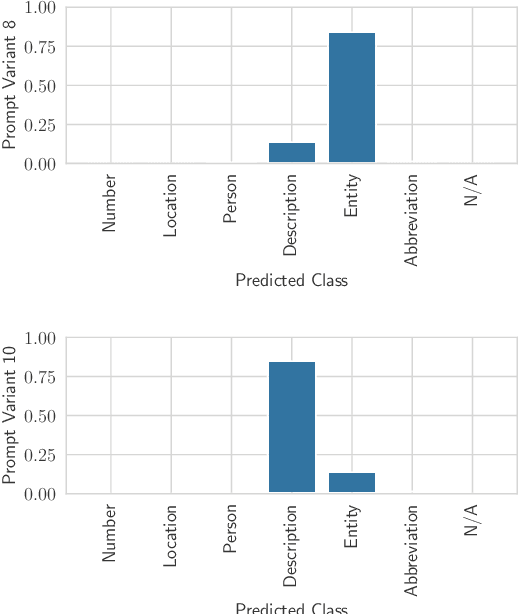
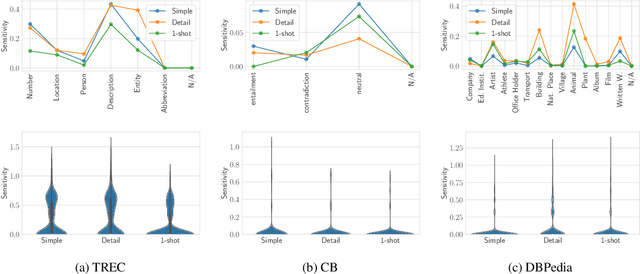
Large Language Models (LLMs) changed the way we design and interact with software systems. Their ability to process and extract information from text has drastically improved productivity in a number of routine tasks. Developers that want to include these models in their software stack, however, face a dreadful challenge: debugging their inconsistent behavior across minor variations of the prompt. We therefore introduce two metrics for classification tasks, namely sensitivity and consistency, which are complementary to task performance. First, sensitivity measures changes of predictions across rephrasings of the prompt, and does not require access to ground truth labels. Instead, consistency measures how predictions vary across rephrasings for elements of the same class. We perform an empirical comparison of these metrics on text classification tasks, using them as guideline for understanding failure modes of the LLM. Our hope is that sensitivity and consistency will be powerful allies in automatic prompt engineering frameworks to obtain LLMs that balance robustness with performance.

Higher-Rank Irreducible Cartesian Tensors for Equivariant Message Passing

The ability to perform fast and accurate atomistic simulations is crucial for advancing the chemical sciences. By learning from high-quality data, machine-learned interatomic potentials achieve accuracy on par with ab initio and first-principles methods at a fraction of their computational cost. The success of machine-learned interatomic potentials arises from integrating inductive biases such as equivariance to group actions on an atomic system, e.g., equivariance to rotations and reflections. In particular, the field has notably advanced with the emergence of equivariant message-passing architectures. Most of these models represent an atomic system using spherical tensors, tensor products of which require complicated numerical coefficients and can be computationally demanding. This work introduces higher-rank irreducible Cartesian tensors as an alternative to spherical tensors, addressing the above limitations. We integrate irreducible Cartesian tensor products into message-passing neural networks and prove the equivariance of the resulting layers. Through empirical evaluations on various benchmark data sets, we consistently observe on-par or better performance than that of state-of-the-art spherical models.

History repeats Itself: A Baseline for Temporal Knowledge Graph Forecasting

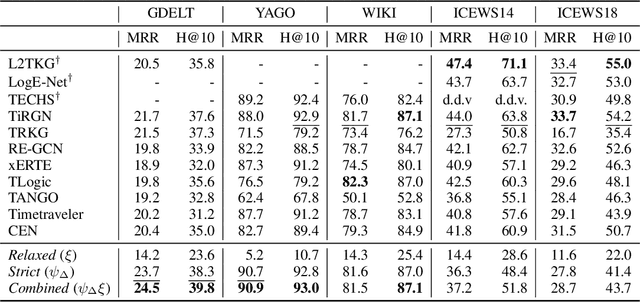
Temporal Knowledge Graph (TKG) Forecasting aims at predicting links in Knowledge Graphs for future timesteps based on a history of Knowledge Graphs. To this day, standardized evaluation protocols and rigorous comparison across TKG models are available, but the importance of simple baselines is often neglected in the evaluation, which prevents researchers from discerning actual and fictitious progress. We propose to close this gap by designing an intuitive baseline for TKG Forecasting based on predicting recurring facts. Compared to most TKG models, it requires little hyperparameter tuning and no iterative training. Further, it can help to identify failure modes in existing approaches. The empirical findings are quite unexpected: compared to 11 methods on five datasets, our baseline ranks first or third in three of them, painting a radically different picture of the predictive quality of the state of the art.

Adaptive Message Passing: A General Framework to Mitigate Oversmoothing, Oversquashing, and Underreaching

Long-range interactions are essential for the correct description of complex systems in many scientific fields. The price to pay for including them in the calculations, however, is a dramatic increase in the overall computational costs. Recently, deep graph networks have been employed as efficient, data-driven surrogate models for predicting properties of complex systems represented as graphs. These models rely on a local and iterative message passing strategy that should, in principle, capture long-range information without explicitly modeling the corresponding interactions. In practice, most deep graph networks cannot really model long-range dependencies due to the intrinsic limitations of (synchronous) message passing, namely oversmoothing, oversquashing, and underreaching. This work proposes a general framework that learns to mitigate these limitations: within a variational inference framework, we endow message passing architectures with the ability to freely adapt their depth and filter messages along the way. With theoretical and empirical arguments, we show that this simple strategy better captures long-range interactions, by surpassing the state of the art on five node and graph prediction datasets suited for this problem. Our approach consistently improves the performances of the baselines tested on these tasks. We complement the exposition with qualitative analyses and ablations to get a deeper understanding of the framework's inner workings.

Uncertainty-biased molecular dynamics for learning uniformly accurate interatomic potentials

Efficiently creating a concise but comprehensive data set for training machine-learned interatomic potentials (MLIPs) is an under-explored problem. Active learning (AL), which uses either biased or unbiased molecular dynamics (MD) simulations to generate candidate pools, aims to address this objective. Existing biased and unbiased MD simulations, however, are prone to miss either rare events or extrapolative regions -- areas of the configurational space where unreliable predictions are made. Simultaneously exploring both regions is necessary for developing uniformly accurate MLIPs. In this work, we demonstrate that MD simulations, when biased by the MLIP's energy uncertainty, effectively capture extrapolative regions and rare events without the need to know \textit{a priori} the system's transition temperatures and pressures. Exploiting automatic differentiation, we enhance bias-forces-driven MD simulations by introducing the concept of bias stress. We also employ calibrated ensemble-free uncertainties derived from sketched gradient features to yield MLIPs with similar or better accuracy than ensemble-based uncertainty methods at a lower computational cost. We use the proposed uncertainty-driven AL approach to develop MLIPs for two benchmark systems: alanine dipeptide and MIL-53(Al). Compared to MLIPs trained with conventional MD simulations, MLIPs trained with the proposed data-generation method more accurately represent the relevant configurational space for both atomic systems.

Self-Tuning Hamiltonian Monte Carlo for Accelerated Sampling

The performance of Hamiltonian Monte Carlo crucially depends on its parameters, in particular the integration timestep and the number of integration steps. We present an adaptive general-purpose framework to automatically tune these parameters based on a loss function which promotes the fast exploration of phase-space. For this, we make use of a fully-differentiable set-up and use backpropagation for optimization. An attention-like loss is defined which allows for the gradient driven learning of the distribution of integration steps. We also highlight the importance of jittering for a smooth loss-surface. Our approach is demonstrated for the one-dimensional harmonic oscillator and alanine dipeptide, a small protein common as a test-case for simulation methods. We find a good correspondence between our loss and the autocorrelation times, resulting in well-tuned parameters for Hamiltonian Monte Carlo.