Optimal Embedding Guided Negative Sample Generation for Knowledge Graph Link Prediction

Knowledge graph embedding (KGE) models encode the structural information of knowledge graphs to predicting new links. Effective training of these models requires distinguishing between positive and negative samples with high precision. Although prior research has shown that improving the quality of negative samples can significantly enhance model accuracy, identifying high-quality negative samples remains a challenging problem. This paper theoretically investigates the condition under which negative samples lead to optimal KG embedding and identifies a sufficient condition for an effective negative sample distribution. Based on this theoretical foundation, we propose \textbf{E}mbedding \textbf{MU}tation (\textsc{EMU}), a novel framework that \emph{generates} negative samples satisfying this condition, in contrast to conventional methods that focus on \emph{identifying} challenging negative samples within the training data. Importantly, the simplicity of \textsc{EMU} ensures seamless integration with existing KGE models and negative sampling methods. To evaluate its efficacy, we conducted comprehensive experiments across multiple datasets. The results consistently demonstrate significant improvements in link prediction performance across various KGE models and negative sampling methods. Notably, \textsc{EMU} enables performance improvements comparable to those achieved by models with embedding dimension five times larger. An implementation of the method and experiments are available at https://github.com/nec-research/EMU-KG.

Fast, Modular, and Differentiable Framework for Machine Learning-Enhanced Molecular Simulations

We present an end-to-end differentiable molecular simulation framework (DIMOS) for molecular dynamics and Monte Carlo simulations. DIMOS easily integrates machine-learning-based interatomic potentials and implements classical force fields including particle-mesh Ewald electrostatics. Thanks to its modularity, both classical and machine-learning-based approaches can be easily combined into a hybrid description of the system (ML/MM). By supporting key molecular dynamics features such as efficient neighborlists and constraint algorithms for larger time steps, the framework bridges the gap between hand-optimized simulation engines and the flexibility of a PyTorch implementation. The superior performance and the high versatility is probed in different benchmarks and applications, with speed-up factors of up to $170\times$. The advantage of differentiability is demonstrated by an end-to-end optimization of the proposal distribution in a Markov Chain Monte Carlo simulation based on Hamiltonian Monte Carlo. Using these optimized simulation parameters a $3\times$ acceleration is observed in comparison to ad-hoc chosen simulation parameters. The code is available at https://github.com/nec-research/DIMOS.

Geometric Kolmogorov-Arnold Superposition Theorem

The Kolmogorov-Arnold Theorem (KAT), or more generally, the Kolmogorov Superposition Theorem (KST), establishes that any non-linear multivariate function can be exactly represented as a finite superposition of non-linear univariate functions. Unlike the universal approximation theorem, which provides only an approximate representation without guaranteeing a fixed network size, KST offers a theoretically exact decomposition. The Kolmogorov-Arnold Network (KAN) was introduced as a trainable model to implement KAT, and recent advancements have adapted KAN using concepts from modern neural networks. However, KAN struggles to effectively model physical systems that require inherent equivariance or invariance to $E(3)$ transformations, a key property for many scientific and engineering applications. In this work, we propose a novel extension of KAT and KAN to incorporate equivariance and invariance over $O(n)$ group actions, enabling accurate and efficient modeling of these systems. Our approach provides a unified approach that bridges the gap between mathematical theory and practical architectures for physical systems, expanding the applicability of KAN to a broader class of problems.

Higher-Rank Irreducible Cartesian Tensors for Equivariant Message Passing

The ability to perform fast and accurate atomistic simulations is crucial for advancing the chemical sciences. By learning from high-quality data, machine-learned interatomic potentials achieve accuracy on par with ab initio and first-principles methods at a fraction of their computational cost. The success of machine-learned interatomic potentials arises from integrating inductive biases such as equivariance to group actions on an atomic system, e.g., equivariance to rotations and reflections. In particular, the field has notably advanced with the emergence of equivariant message-passing architectures. Most of these models represent an atomic system using spherical tensors, tensor products of which require complicated numerical coefficients and can be computationally demanding. This work introduces higher-rank irreducible Cartesian tensors as an alternative to spherical tensors, addressing the above limitations. We integrate irreducible Cartesian tensor products into message-passing neural networks and prove the equivariance of the resulting layers. Through empirical evaluations on various benchmark data sets, we consistently observe on-par or better performance than that of state-of-the-art spherical models.

Compositional Generative Inverse Design

Inverse design, where we seek to design input variables in order to optimize an underlying objective function, is an important problem that arises across fields such as mechanical engineering to aerospace engineering. Inverse design is typically formulated as an optimization problem, with recent works leveraging optimization across learned dynamics models. However, as models are optimized they tend to fall into adversarial modes, preventing effective sampling. We illustrate that by instead optimizing over the learned energy function captured by the diffusion model, we can avoid such adversarial examples and significantly improve design performance. We further illustrate how such a design system is compositional, enabling us to combine multiple different diffusion models representing subcomponents of our desired system to design systems with every specified component. In an N-body interaction task and a challenging 2D multi-airfoil design task, we demonstrate that by composing the learned diffusion model at test time, our method allows us to design initial states and boundary shapes that are more complex than those in the training data. Our method outperforms state-of-the-art neural inverse design method by an average of 41.5% in prediction MAE and 14.3% in design objective for the N-body dataset and discovers formation flying to minimize drag in the multi-airfoil design task. Project website and code can be found at https://github.com/AI4Science-WestlakeU/cindm.

Adaptive Message Passing: A General Framework to Mitigate Oversmoothing, Oversquashing, and Underreaching

Long-range interactions are essential for the correct description of complex systems in many scientific fields. The price to pay for including them in the calculations, however, is a dramatic increase in the overall computational costs. Recently, deep graph networks have been employed as efficient, data-driven surrogate models for predicting properties of complex systems represented as graphs. These models rely on a local and iterative message passing strategy that should, in principle, capture long-range information without explicitly modeling the corresponding interactions. In practice, most deep graph networks cannot really model long-range dependencies due to the intrinsic limitations of (synchronous) message passing, namely oversmoothing, oversquashing, and underreaching. This work proposes a general framework that learns to mitigate these limitations: within a variational inference framework, we endow message passing architectures with the ability to freely adapt their depth and filter messages along the way. With theoretical and empirical arguments, we show that this simple strategy better captures long-range interactions, by surpassing the state of the art on five node and graph prediction datasets suited for this problem. Our approach consistently improves the performances of the baselines tested on these tasks. We complement the exposition with qualitative analyses and ablations to get a deeper understanding of the framework's inner workings.

Learning Controllable Adaptive Simulation for Multi-resolution Physics

Simulating the time evolution of physical systems is pivotal in many scientific and engineering problems. An open challenge in simulating such systems is their multi-resolution dynamics: a small fraction of the system is extremely dynamic, and requires very fine-grained resolution, while a majority of the system is changing slowly and can be modeled by coarser spatial scales. Typical learning-based surrogate models use a uniform spatial scale, which needs to resolve to the finest required scale and can waste a huge compute to achieve required accuracy. In this work, we introduce Learning controllable Adaptive simulation for Multi-resolution Physics (LAMP) as the first full deep learning-based surrogate model that jointly learns the evolution model and optimizes appropriate spatial resolutions that devote more compute to the highly dynamic regions. LAMP consists of a Graph Neural Network (GNN) for learning the forward evolution, and a GNN-based actor-critic for learning the policy of spatial refinement and coarsening. We introduce learning techniques that optimizes LAMP with weighted sum of error and computational cost as objective, allowing LAMP to adapt to varying relative importance of error vs. computation tradeoff at inference time. We evaluate our method in a 1D benchmark of nonlinear PDEs and a challenging 2D mesh-based simulation. We demonstrate that our LAMP outperforms state-of-the-art deep learning surrogate models, and can adaptively trade-off computation to improve long-term prediction error: it achieves an average of 33.7% error reduction for 1D nonlinear PDEs, and outperforms MeshGraphNets + classical Adaptive Mesh Refinement (AMR) in 2D mesh-based simulations. Project website with data and code can be found at: http://snap.stanford.edu/lamp.

Learning to Accelerate Partial Differential Equations via Latent Global Evolution

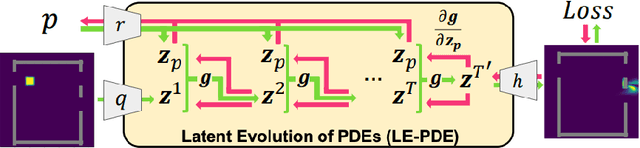
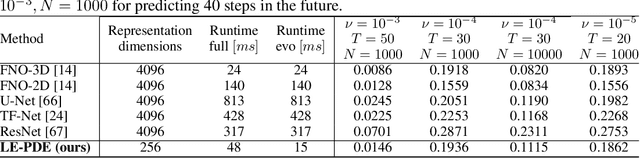
Simulating the time evolution of Partial Differential Equations (PDEs) of large-scale systems is crucial in many scientific and engineering domains such as fluid dynamics, weather forecasting and their inverse optimization problems. However, both classical solvers and recent deep learning-based surrogate models are typically extremely computationally intensive, because of their local evolution: they need to update the state of each discretized cell at each time step during inference. Here we develop Latent Evolution of PDEs (LE-PDE), a simple, fast and scalable method to accelerate the simulation and inverse optimization of PDEs. LE-PDE learns a compact, global representation of the system and efficiently evolves it fully in the latent space with learned latent evolution models. LE-PDE achieves speed-up by having a much smaller latent dimension to update during long rollout as compared to updating in the input space. We introduce new learning objectives to effectively learn such latent dynamics to ensure long-term stability. We further introduce techniques for speeding-up inverse optimization of boundary conditions for PDEs via backpropagation through time in latent space, and an annealing technique to address the non-differentiability and sparse interaction of boundary conditions. We test our method in a 1D benchmark of nonlinear PDEs, 2D Navier-Stokes flows into turbulent phase and an inverse optimization of boundary conditions in 2D Navier-Stokes flow. Compared to state-of-the-art deep learning-based surrogate models and other strong baselines, we demonstrate up to 128x reduction in the dimensions to update, and up to 15x improvement in speed, while achieving competitive accuracy.