GGBall: Graph Generative Model on Poincaré Ball

Generating graphs with hierarchical structures remains a fundamental challenge due to the limitations of Euclidean geometry in capturing exponential complexity. Here we introduce \textbf{GGBall}, a novel hyperbolic framework for graph generation that integrates geometric inductive biases with modern generative paradigms. GGBall combines a Hyperbolic Vector-Quantized Autoencoder (HVQVAE) with a Riemannian flow matching prior defined via closed-form geodesics. This design enables flow-based priors to model complex latent distributions, while vector quantization helps preserve the curvature-aware structure of the hyperbolic space. We further develop a suite of hyperbolic GNN and Transformer layers that operate entirely within the manifold, ensuring stability and scalability. Empirically, our model reduces degree MMD by over 75\% on Community-Small and over 40\% on Ego-Small compared to state-of-the-art baselines, demonstrating an improved ability to preserve topological hierarchies. These results highlight the potential of hyperbolic geometry as a powerful foundation for the generative modeling of complex, structured, and hierarchical data domains. Our code is available at \href{https://github.com/AI4Science-WestlakeU/GGBall}{here}.

EqCollide: Equivariant and Collision-Aware Deformable Objects Neural Simulator

Simulating collisions of deformable objects is a fundamental yet challenging task due to the complexity of modeling solid mechanics and multi-body interactions. Existing data-driven methods often suffer from lack of equivariance to physical symmetries, inadequate handling of collisions, and limited scalability. Here we introduce EqCollide, the first end-to-end equivariant neural fields simulator for deformable objects and their collisions. We propose an equivariant encoder to map object geometry and velocity into latent control points. A subsequent equivariant Graph Neural Network-based Neural Ordinary Differential Equation models the interactions among control points via collision-aware message passing. To reconstruct velocity fields, we query a neural field conditioned on control point features, enabling continuous and resolution-independent motion predictions. Experimental results show that EqCollide achieves accurate, stable, and scalable simulations across diverse object configurations, and our model achieves 24.34% to 35.82% lower rollout MSE even compared with the best-performing baseline model. Furthermore, our model could generalize to more colliding objects and extended temporal horizons, and stay robust to input transformed with group action.

From Uncertain to Safe: Conformal Fine-Tuning of Diffusion Models for Safe PDE Control

The application of deep learning for partial differential equation (PDE)-constrained control is gaining increasing attention. However, existing methods rarely consider safety requirements crucial in real-world applications. To address this limitation, we propose Safe Diffusion Models for PDE Control (SafeDiffCon), which introduce the uncertainty quantile as model uncertainty quantification to achieve optimal control under safety constraints through both post-training and inference phases. Firstly, our approach post-trains a pre-trained diffusion model to generate control sequences that better satisfy safety constraints while achieving improved control objectives via a reweighted diffusion loss, which incorporates the uncertainty quantile estimated using conformal prediction. Secondly, during inference, the diffusion model dynamically adjusts both its generation process and parameters through iterative guidance and fine-tuning, conditioned on control targets while simultaneously integrating the estimated uncertainty quantile. We evaluate SafeDiffCon on three control tasks: 1D Burgers' equation, 2D incompressible fluid, and controlled nuclear fusion problem. Results demonstrate that SafeDiffCon is the only method that satisfies all safety constraints, whereas other classical and deep learning baselines fail. Furthermore, while adhering to safety constraints, SafeDiffCon achieves the best control performance.

On the Guidance of Flow Matching

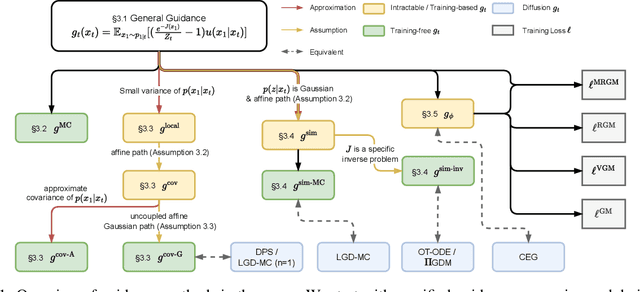
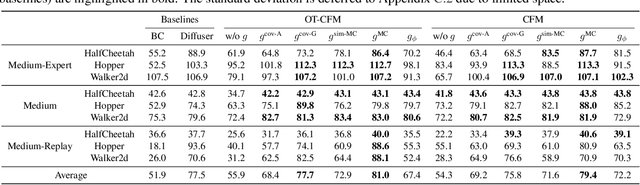
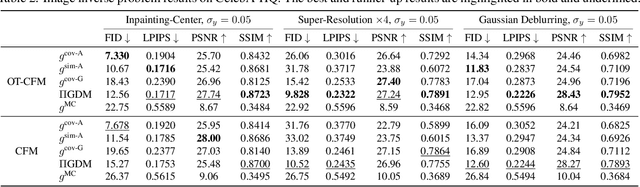
Flow matching has shown state-of-the-art performance in various generative tasks, ranging from image generation to decision-making, where guided generation is pivotal. However, the guidance of flow matching is more general than and thus substantially different from that of its predecessor, diffusion models. Therefore, the challenge in guidance for general flow matching remains largely underexplored. In this paper, we propose the first framework of general guidance for flow matching. From this framework, we derive a family of guidance techniques that can be applied to general flow matching. These include a new training-free asymptotically exact guidance, novel training losses for training-based guidance, and two classes of approximate guidance that cover classical gradient guidance methods as special cases. We theoretically investigate these different methods to give a practical guideline for choosing suitable methods in different scenarios. Experiments on synthetic datasets, image inverse problems, and offline reinforcement learning demonstrate the effectiveness of our proposed guidance methods and verify the correctness of our flow matching guidance framework. Code to reproduce the experiments can be found at https://github.com/AI4Science-WestlakeU/flow_guidance.

T-SCEND: Test-time Scalable MCTS-enhanced Diffusion Model

We introduce Test-time Scalable MCTS-enhanced Diffusion Model (T-SCEND), a novel framework that significantly improves diffusion model's reasoning capabilities with better energy-based training and scaling up test-time computation. We first show that na\"ively scaling up inference budget for diffusion models yields marginal gain. To address this, the training of T-SCEND consists of a novel linear-regression negative contrastive learning objective to improve the performance-energy consistency of the energy landscape, and a KL regularization to reduce adversarial sampling. During inference, T-SCEND integrates the denoising process with a novel hybrid Monte Carlo Tree Search (hMCTS), which sequentially performs best-of-N random search and MCTS as denoising proceeds. On challenging reasoning tasks of Maze and Sudoku, we demonstrate the effectiveness of T-SCEND's training objective and scalable inference method. In particular, trained with Maze sizes of up to $6\times6$, our T-SCEND solves $88\%$ of Maze problems with much larger sizes of $15\times15$, while standard diffusion completely fails.Code to reproduce the experiments can be found at https://github.com/AI4Science-WestlakeU/t_scend.

Wavelet Diffusion Neural Operator

Simulating and controlling physical systems described by partial differential equations (PDEs) are crucial tasks across science and engineering. Recently, diffusion generative models have emerged as a competitive class of methods for these tasks due to their ability to capture long-term dependencies and model high-dimensional states. However, diffusion models typically struggle with handling system states with abrupt changes and generalizing to higher resolutions. In this work, we propose Wavelet Diffusion Neural Operator (WDNO), a novel PDE simulation and control framework that enhances the handling of these complexities. WDNO comprises two key innovations. Firstly, WDNO performs diffusion-based generative modeling in the wavelet domain for the entire trajectory to handle abrupt changes and long-term dependencies effectively. Secondly, to address the issue of poor generalization across different resolutions, which is one of the fundamental tasks in modeling physical systems, we introduce multi-resolution training. We validate WDNO on five physical systems, including 1D advection equation, three challenging physical systems with abrupt changes (1D Burgers' equation, 1D compressible Navier-Stokes equation and 2D incompressible fluid), and a real-world dataset ERA5, which demonstrates superior performance on both simulation and control tasks over state-of-the-art methods, with significant improvements in long-term and detail prediction accuracy. Remarkably, in the challenging context of the 2D high-dimensional and indirect control task aimed at reducing smoke leakage, WDNO reduces the leakage by 33.2% compared to the second-best baseline.

Compositional Generative Multiphysics and Multi-component Simulation

Multiphysics simulation, which models the interactions between multiple physical processes, and multi-component simulation of complex structures are critical in fields like nuclear and aerospace engineering. Previous studies often rely on numerical solvers or machine learning-based surrogate models to solve or accelerate these simulations. However, multiphysics simulations typically require integrating multiple specialized solvers-each responsible for evolving a specific physical process-into a coupled program, which introduces significant development challenges. Furthermore, no universal algorithm exists for multi-component simulations, which adds to the complexity. Here we propose compositional Multiphysics and Multi-component Simulation with Diffusion models (MultiSimDiff) to overcome these challenges. During diffusion-based training, MultiSimDiff learns energy functions modeling the conditional probability of one physical process/component conditioned on other processes/components. In inference, MultiSimDiff generates coupled multiphysics solutions and multi-component structures by sampling from the joint probability distribution, achieved by composing the learned energy functions in a structured way. We test our method in three tasks. In the reaction-diffusion and nuclear thermal coupling problems, MultiSimDiff successfully predicts the coupling solution using decoupled data, while the surrogate model fails in the more complex second problem. For the thermal and mechanical analysis of the prismatic fuel element, MultiSimDiff trained for single component prediction accurately predicts a larger structure with 64 components, reducing the relative error by 40.3% compared to the surrogate model.

Recent Advances on Machine Learning for Computational Fluid Dynamics: A Survey

This paper explores the recent advancements in enhancing Computational Fluid Dynamics (CFD) tasks through Machine Learning (ML) techniques. We begin by introducing fundamental concepts, traditional methods, and benchmark datasets, then examine the various roles ML plays in improving CFD. The literature systematically reviews papers in recent five years and introduces a novel classification for forward modeling: Data-driven Surrogates, Physics-Informed Surrogates, and ML-assisted Numerical Solutions. Furthermore, we also review the latest ML methods in inverse design and control, offering a novel classification and providing an in-depth discussion. Then we highlight real-world applications of ML for CFD in critical scientific and engineering disciplines, including aerodynamics, combustion, atmosphere & ocean science, biology fluid, plasma, symbolic regression, and reduced order modeling. Besides, we identify key challenges and advocate for future research directions to address these challenges, such as multi-scale representation, physical knowledge encoding, scientific foundation model and automatic scientific discovery. This review serves as a guide for the rapidly expanding ML for CFD community, aiming to inspire insights for future advancements. We draw the conclusion that ML is poised to significantly transform CFD research by enhancing simulation accuracy, reducing computational time, and enabling more complex analyses of fluid dynamics. The paper resources can be viewed at https://github.com/WillDreamer/Awesome-AI4CFD.

Closed-loop Diffusion Control of Complex Physical Systems

The control problems of complex physical systems have wide applications in science and engineering. Several previous works have demonstrated that generative control methods based on diffusion models have significant advantages for solving these problems. However, existing generative control methods face challenges in handling closed-loop control, which is an inherent constraint for effective control of complex physical systems. In this paper, we propose a Closed-Loop Diffusion method for Physical systems Control (CL-DiffPhyCon). By adopting an asynchronous denoising schedule for different time steps, CL-DiffPhyCon generates control signals conditioned on real-time feedback from the environment. Thus, CL-DiffPhyCon is able to speed up diffusion control methods in a closed-loop framework. We evaluate CL-DiffPhyCon on the 1D Burgers' equation control and 2D incompressible fluid control tasks. The results demonstrate that CL-DiffPhyCon achieves notable control performance with significant sampling acceleration.

A Generative Approach to Control Complex Physical Systems

Controlling the evolution of complex physical systems is a fundamental task across science and engineering. Classical techniques suffer from limited applicability or huge computational costs. On the other hand, recent deep learning and reinforcement learning-based approaches often struggle to optimize long-term control sequences under the constraints of system dynamics. In this work, we introduce Diffusion Physical systems Control (DiffPhyCon), a new class of method to address the physical systems control problem. DiffPhyCon excels by simultaneously minimizing both the learned generative energy function and the predefined control objectives across the entire trajectory and control sequence. Thus, it can explore globally and identify near-optimal control sequences. Moreover, we enhance DiffPhyCon with prior reweighting, enabling the discovery of control sequences that significantly deviate from the training distribution. We test our method in 1D Burgers' equation and 2D jellyfish movement control in a fluid environment. Our method outperforms widely applied classical approaches and state-of-the-art deep learning and reinforcement learning methods. Notably, DiffPhyCon unveils an intriguing fast-close-slow-open pattern observed in the jellyfish, aligning with established findings in the field of fluid dynamics.