Zhi-Ming Ma
RealPDEBench: A Benchmark for Complex Physical Systems with Real-World Data
Jan 05, 2026Abstract:Predicting the evolution of complex physical systems remains a central problem in science and engineering. Despite rapid progress in scientific Machine Learning (ML) models, a critical bottleneck is the lack of expensive real-world data, resulting in most current models being trained and validated on simulated data. Beyond limiting the development and evaluation of scientific ML, this gap also hinders research into essential tasks such as sim-to-real transfer. We introduce RealPDEBench, the first benchmark for scientific ML that integrates real-world measurements with paired numerical simulations. RealPDEBench consists of five datasets, three tasks, eight metrics, and ten baselines. We first present five real-world measured datasets with paired simulated datasets across different complex physical systems. We further define three tasks, which allow comparisons between real-world and simulated data, and facilitate the development of methods to bridge the two. Moreover, we design eight evaluation metrics, spanning data-oriented and physics-oriented metrics, and finally benchmark ten representative baselines, including state-of-the-art models, pretrained PDE foundation models, and a traditional method. Experiments reveal significant discrepancies between simulated and real-world data, while showing that pretraining with simulated data consistently improves both accuracy and convergence. In this work, we hope to provide insights from real-world data, advancing scientific ML toward bridging the sim-to-real gap and real-world deployment. Our benchmark, datasets, and instructions are available at https://realpdebench.github.io/.
OmniFluids: Unified Physics Pre-trained Modeling of Fluid Dynamics
Jun 12, 2025Abstract:High-fidelity and efficient simulation of fluid dynamics drive progress in various scientific and engineering applications. Traditional computational fluid dynamics methods offer strong interpretability and guaranteed convergence, but rely on fine spatial and temporal meshes, incurring prohibitive computational costs. Physics-informed neural networks (PINNs) and neural operators aim to accelerate PDE solvers using deep learning techniques. However, PINNs require extensive retraining and careful tuning, and purely data-driven operators demand large labeled datasets. Hybrid physics-aware methods embed numerical discretizations into network architectures or loss functions, but achieve marginal speed gains and become unstable when balancing coarse priors against high-fidelity measurements. To this end, we introduce OmniFluids, a unified physics pre-trained operator learning framework that integrates physics-only pre-training, coarse-grid operator distillation, and few-shot fine-tuning, which enables fast inference and accurate prediction under limited or zero data supervision. For architectural design, the key components of OmniFluids include a mixture of operators, a multi-frame decoder, and factorized Fourier layers, which enable efficient and scalable modeling of diverse physical tasks while maintaining seamless integration with physics-based supervision. Across a broad range of two- and three-dimensional benchmarks, OmniFluids significantly outperforms state-of-the-art AI-driven methods in flow field reconstruction and turbulence statistics accuracy, delivering 10-100x speedups compared to classical solvers, and accurately recovers unknown physical parameters from sparse, noisy data. This work establishes a new paradigm for efficient and generalizable surrogate modeling in complex fluid systems under limited data availability.
Graffe: Graph Representation Learning via Diffusion Probabilistic Models
May 08, 2025Abstract:Diffusion probabilistic models (DPMs), widely recognized for their potential to generate high-quality samples, tend to go unnoticed in representation learning. While recent progress has highlighted their potential for capturing visual semantics, adapting DPMs to graph representation learning remains in its infancy. In this paper, we introduce Graffe, a self-supervised diffusion model proposed for graph representation learning. It features a graph encoder that distills a source graph into a compact representation, which, in turn, serves as the condition to guide the denoising process of the diffusion decoder. To evaluate the effectiveness of our model, we first explore the theoretical foundations of applying diffusion models to representation learning, proving that the denoising objective implicitly maximizes the conditional mutual information between data and its representation. Specifically, we prove that the negative logarithm of the denoising score matching loss is a tractable lower bound for the conditional mutual information. Empirically, we conduct a series of case studies to validate our theoretical insights. In addition, Graffe delivers competitive results under the linear probing setting on node and graph classification tasks, achieving state-of-the-art performance on 9 of the 11 real-world datasets. These findings indicate that powerful generative models, especially diffusion models, serve as an effective tool for graph representation learning.
Riemannian Neural Geodesic Interpolant
Apr 22, 2025

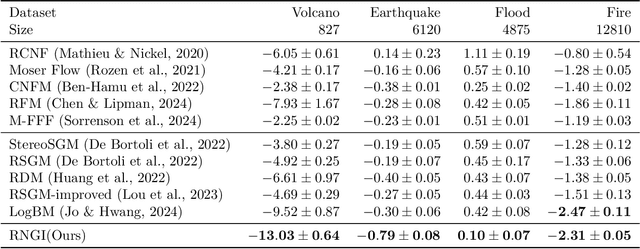

Abstract:Stochastic interpolants are efficient generative models that bridge two arbitrary probability density functions in finite time, enabling flexible generation from the source to the target distribution or vice versa. These models are primarily developed in Euclidean space, and are therefore limited in their application to many distribution learning problems defined on Riemannian manifolds in real-world scenarios. In this work, we introduce the Riemannian Neural Geodesic Interpolant (RNGI) model, which interpolates between two probability densities on a Riemannian manifold along the stochastic geodesics, and then samples from one endpoint as the final state using the continuous flow originating from the other endpoint. We prove that the temporal marginal density of RNGI solves a transport equation on the Riemannian manifold. After training the model's the neural velocity and score fields, we propose the Embedding Stochastic Differential Equation (E-SDE) algorithm for stochastic sampling of RNGI. E-SDE significantly improves the sampling quality by reducing the accumulated error caused by the excessive intrinsic discretization of Riemannian Brownian motion in the classical Geodesic Random Walk (GRW) algorithm. We also provide theoretical bounds on the generative bias measured in terms of KL-divergence. Finally, we demonstrate the effectiveness of the proposed RNGI and E-SDE through experiments conducted on both collected and synthetic distributions on S2 and SO(3).
Straight-Line Diffusion Model for Efficient 3D Molecular Generation
Mar 04, 2025Abstract:Diffusion-based models have shown great promise in molecular generation but often require a large number of sampling steps to generate valid samples. In this paper, we introduce a novel Straight-Line Diffusion Model (SLDM) to tackle this problem, by formulating the diffusion process to follow a linear trajectory. The proposed process aligns well with the noise sensitivity characteristic of molecular structures and uniformly distributes reconstruction effort across the generative process, thus enhancing learning efficiency and efficacy. Consequently, SLDM achieves state-of-the-art performance on 3D molecule generation benchmarks, delivering a 100-fold improvement in sampling efficiency. Furthermore, experiments on toy data and image generation tasks validate the generality and robustness of SLDM, showcasing its potential across diverse generative modeling domains.
Improved Diffusion-based Generative Model with Better Adversarial Robustness
Feb 24, 2025Abstract:Diffusion Probabilistic Models (DPMs) have achieved significant success in generative tasks. However, their training and sampling processes suffer from the issue of distribution mismatch. During the denoising process, the input data distributions differ between the training and inference stages, potentially leading to inaccurate data generation. To obviate this, we analyze the training objective of DPMs and theoretically demonstrate that this mismatch can be alleviated through Distributionally Robust Optimization (DRO), which is equivalent to performing robustness-driven Adversarial Training (AT) on DPMs. Furthermore, for the recently proposed Consistency Model (CM), which distills the inference process of the DPM, we prove that its training objective also encounters the mismatch issue. Fortunately, this issue can be mitigated by AT as well. Based on these insights, we propose to conduct efficient AT on both DPM and CM. Finally, extensive empirical studies validate the effectiveness of AT in diffusion-based models. The code is available at https://github.com/kugwzk/AT_Diff.
From Uncertain to Safe: Conformal Fine-Tuning of Diffusion Models for Safe PDE Control
Feb 04, 2025



Abstract:The application of deep learning for partial differential equation (PDE)-constrained control is gaining increasing attention. However, existing methods rarely consider safety requirements crucial in real-world applications. To address this limitation, we propose Safe Diffusion Models for PDE Control (SafeDiffCon), which introduce the uncertainty quantile as model uncertainty quantification to achieve optimal control under safety constraints through both post-training and inference phases. Firstly, our approach post-trains a pre-trained diffusion model to generate control sequences that better satisfy safety constraints while achieving improved control objectives via a reweighted diffusion loss, which incorporates the uncertainty quantile estimated using conformal prediction. Secondly, during inference, the diffusion model dynamically adjusts both its generation process and parameters through iterative guidance and fine-tuning, conditioned on control targets while simultaneously integrating the estimated uncertainty quantile. We evaluate SafeDiffCon on three control tasks: 1D Burgers' equation, 2D incompressible fluid, and controlled nuclear fusion problem. Results demonstrate that SafeDiffCon is the only method that satisfies all safety constraints, whereas other classical and deep learning baselines fail. Furthermore, while adhering to safety constraints, SafeDiffCon achieves the best control performance.
Wavelet Diffusion Neural Operator
Dec 06, 2024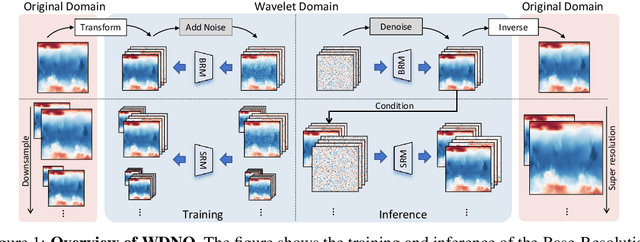
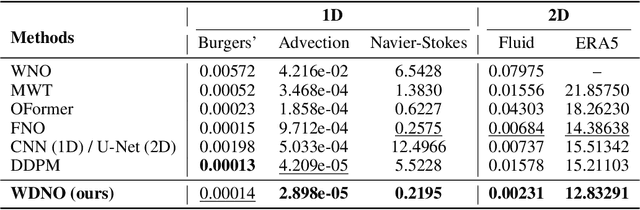
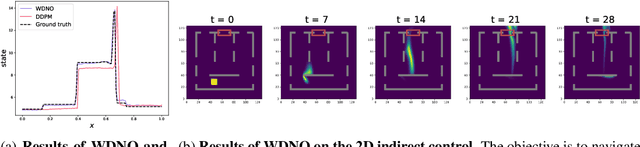
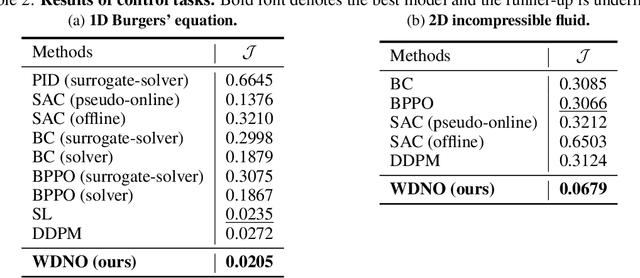
Abstract:Simulating and controlling physical systems described by partial differential equations (PDEs) are crucial tasks across science and engineering. Recently, diffusion generative models have emerged as a competitive class of methods for these tasks due to their ability to capture long-term dependencies and model high-dimensional states. However, diffusion models typically struggle with handling system states with abrupt changes and generalizing to higher resolutions. In this work, we propose Wavelet Diffusion Neural Operator (WDNO), a novel PDE simulation and control framework that enhances the handling of these complexities. WDNO comprises two key innovations. Firstly, WDNO performs diffusion-based generative modeling in the wavelet domain for the entire trajectory to handle abrupt changes and long-term dependencies effectively. Secondly, to address the issue of poor generalization across different resolutions, which is one of the fundamental tasks in modeling physical systems, we introduce multi-resolution training. We validate WDNO on five physical systems, including 1D advection equation, three challenging physical systems with abrupt changes (1D Burgers' equation, 1D compressible Navier-Stokes equation and 2D incompressible fluid), and a real-world dataset ERA5, which demonstrates superior performance on both simulation and control tasks over state-of-the-art methods, with significant improvements in long-term and detail prediction accuracy. Remarkably, in the challenging context of the 2D high-dimensional and indirect control task aimed at reducing smoke leakage, WDNO reduces the leakage by 33.2% compared to the second-best baseline.
UniGEM: A Unified Approach to Generation and Property Prediction for Molecules
Oct 14, 2024



Abstract:Molecular generation and molecular property prediction are both crucial for drug discovery, but they are often developed independently. Inspired by recent studies, which demonstrate that diffusion model, a prominent generative approach, can learn meaningful data representations that enhance predictive tasks, we explore the potential for developing a unified generative model in the molecular domain that effectively addresses both molecular generation and property prediction tasks. However, the integration of these tasks is challenging due to inherent inconsistencies, making simple multi-task learning ineffective. To address this, we propose UniGEM, the first unified model to successfully integrate molecular generation and property prediction, delivering superior performance in both tasks. Our key innovation lies in a novel two-phase generative process, where predictive tasks are activated in the later stages, after the molecular scaffold is formed. We further enhance task balance through innovative training strategies. Rigorous theoretical analysis and comprehensive experiments demonstrate our significant improvements in both tasks. The principles behind UniGEM hold promise for broader applications, including natural language processing and computer vision.
Recent Advances on Machine Learning for Computational Fluid Dynamics: A Survey
Aug 22, 2024Abstract:This paper explores the recent advancements in enhancing Computational Fluid Dynamics (CFD) tasks through Machine Learning (ML) techniques. We begin by introducing fundamental concepts, traditional methods, and benchmark datasets, then examine the various roles ML plays in improving CFD. The literature systematically reviews papers in recent five years and introduces a novel classification for forward modeling: Data-driven Surrogates, Physics-Informed Surrogates, and ML-assisted Numerical Solutions. Furthermore, we also review the latest ML methods in inverse design and control, offering a novel classification and providing an in-depth discussion. Then we highlight real-world applications of ML for CFD in critical scientific and engineering disciplines, including aerodynamics, combustion, atmosphere & ocean science, biology fluid, plasma, symbolic regression, and reduced order modeling. Besides, we identify key challenges and advocate for future research directions to address these challenges, such as multi-scale representation, physical knowledge encoding, scientific foundation model and automatic scientific discovery. This review serves as a guide for the rapidly expanding ML for CFD community, aiming to inspire insights for future advancements. We draw the conclusion that ML is poised to significantly transform CFD research by enhancing simulation accuracy, reducing computational time, and enabling more complex analyses of fluid dynamics. The paper resources can be viewed at https://github.com/WillDreamer/Awesome-AI4CFD.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge