OmniFluids: Unified Physics Pre-trained Modeling of Fluid Dynamics

High-fidelity and efficient simulation of fluid dynamics drive progress in various scientific and engineering applications. Traditional computational fluid dynamics methods offer strong interpretability and guaranteed convergence, but rely on fine spatial and temporal meshes, incurring prohibitive computational costs. Physics-informed neural networks (PINNs) and neural operators aim to accelerate PDE solvers using deep learning techniques. However, PINNs require extensive retraining and careful tuning, and purely data-driven operators demand large labeled datasets. Hybrid physics-aware methods embed numerical discretizations into network architectures or loss functions, but achieve marginal speed gains and become unstable when balancing coarse priors against high-fidelity measurements. To this end, we introduce OmniFluids, a unified physics pre-trained operator learning framework that integrates physics-only pre-training, coarse-grid operator distillation, and few-shot fine-tuning, which enables fast inference and accurate prediction under limited or zero data supervision. For architectural design, the key components of OmniFluids include a mixture of operators, a multi-frame decoder, and factorized Fourier layers, which enable efficient and scalable modeling of diverse physical tasks while maintaining seamless integration with physics-based supervision. Across a broad range of two- and three-dimensional benchmarks, OmniFluids significantly outperforms state-of-the-art AI-driven methods in flow field reconstruction and turbulence statistics accuracy, delivering 10-100x speedups compared to classical solvers, and accurately recovers unknown physical parameters from sparse, noisy data. This work establishes a new paradigm for efficient and generalizable surrogate modeling in complex fluid systems under limited data availability.

SPDEBench: An Extensive Benchmark for Learning Regular and Singular Stochastic PDEs

Stochastic Partial Differential Equations (SPDEs) driven by random noise play a central role in modelling physical processes whose spatio-temporal dynamics can be rough, such as turbulence flows, superconductors, and quantum dynamics. To efficiently model these processes and make predictions, machine learning (ML)-based surrogate models are proposed, with their network architectures incorporating the spatio-temporal roughness in their design. However, it lacks an extensive and unified datasets for SPDE learning; especially, existing datasets do not account for the computational error introduced by noise sampling and the necessary renormalization required for handling singular SPDEs. We thus introduce SPDEBench, which is designed to solve typical SPDEs of physical significance (e.g., the $\Phi^4_d$, wave, incompressible Navier--Stokes, and KdV equations) on 1D or 2D tori driven by white noise via ML methods. New datasets for singular SPDEs based on the renormalization process have been constructed, and novel ML models achieving the best results to date have been proposed. In particular, we investigate the impact of computational error introduced by noise sampling and renormalization on the performance comparison of ML models and highlight the importance of selecting high-quality test data for accurate evaluation. Results are benchmarked with traditional numerical solvers and ML-based models, including FNO, NSPDE and DLR-Net, etc. It is shown that, for singular SPDEs, naively applying ML models on data without specifying the numerical schemes can lead to significant errors and misleading conclusions. Our SPDEBench provides an open-source codebase that ensures full reproducibility of benchmarking across a variety of SPDE datasets while offering the flexibility to incorporate new datasets and machine learning baselines, making it a valuable resource for the community.

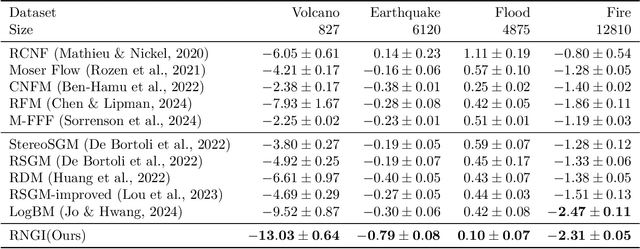
Riemannian Neural Geodesic Interpolant

Stochastic interpolants are efficient generative models that bridge two arbitrary probability density functions in finite time, enabling flexible generation from the source to the target distribution or vice versa. These models are primarily developed in Euclidean space, and are therefore limited in their application to many distribution learning problems defined on Riemannian manifolds in real-world scenarios. In this work, we introduce the Riemannian Neural Geodesic Interpolant (RNGI) model, which interpolates between two probability densities on a Riemannian manifold along the stochastic geodesics, and then samples from one endpoint as the final state using the continuous flow originating from the other endpoint. We prove that the temporal marginal density of RNGI solves a transport equation on the Riemannian manifold. After training the model's the neural velocity and score fields, we propose the Embedding Stochastic Differential Equation (E-SDE) algorithm for stochastic sampling of RNGI. E-SDE significantly improves the sampling quality by reducing the accumulated error caused by the excessive intrinsic discretization of Riemannian Brownian motion in the classical Geodesic Random Walk (GRW) algorithm. We also provide theoretical bounds on the generative bias measured in terms of KL-divergence. Finally, we demonstrate the effectiveness of the proposed RNGI and E-SDE through experiments conducted on both collected and synthetic distributions on S2 and SO(3).

HR-Extreme: A High-Resolution Dataset for Extreme Weather Forecasting

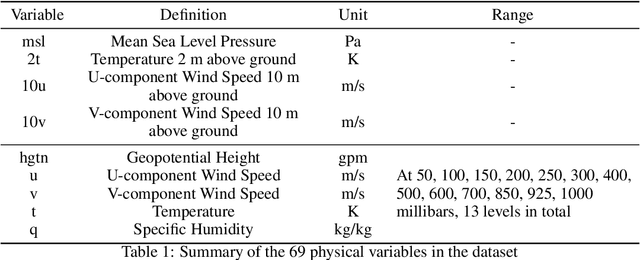
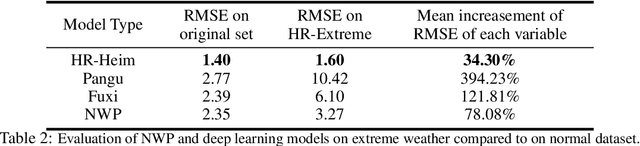
The application of large deep learning models in weather forecasting has led to significant advancements in the field, including higher-resolution forecasting and extended prediction periods exemplified by models such as Pangu and Fuxi. Despite these successes, previous research has largely been characterized by the neglect of extreme weather events, and the availability of datasets specifically curated for such events remains limited. Given the critical importance of accurately forecasting extreme weather, this study introduces a comprehensive dataset that incorporates high-resolution extreme weather cases derived from the High-Resolution Rapid Refresh (HRRR) data, a 3-km real-time dataset provided by NOAA. We also evaluate the current state-of-the-art deep learning models and Numerical Weather Prediction (NWP) systems on HR-Extreme, and provide a improved baseline deep learning model called HR-Heim which has superior performance on both general loss and HR-Extreme compared to others. Our results reveal that the errors of extreme weather cases are significantly larger than overall forecast error, highlighting them as an crucial source of loss in weather prediction. These findings underscore the necessity for future research to focus on improving the accuracy of extreme weather forecasts to enhance their practical utility.

MEFT: Memory-Efficient Fine-Tuning through Sparse Adapter

Parameter-Efficient Fine-tuning (PEFT) facilitates the fine-tuning of Large Language Models (LLMs) under limited resources. However, the fine-tuning performance with PEFT on complex, knowledge-intensive tasks is limited due to the constrained model capacity, which originates from the limited number of additional trainable parameters. To overcome this limitation, we introduce a novel mechanism that fine-tunes LLMs with adapters of larger size yet memory-efficient. This is achieved by leveraging the inherent activation sparsity in the Feed-Forward Networks (FFNs) of LLMs and utilizing the larger capacity of Central Processing Unit (CPU) memory compared to Graphics Processing Unit (GPU). We store and update the parameters of larger adapters on the CPU. Moreover, we employ a Mixture of Experts (MoE)-like architecture to mitigate unnecessary CPU computations and reduce the communication volume between the GPU and CPU. This is particularly beneficial over the limited bandwidth of PCI Express (PCIe). Our method can achieve fine-tuning results comparable to those obtained with larger memory capacities, even when operating under more limited resources such as a 24GB memory single GPU setup, with acceptable loss in training efficiency. Our codes are available at https://github.com/CURRENTF/MEFT.

On the Convergence of Adam under Non-uniform Smoothness: Separability from SGDM and Beyond

This paper aims to clearly distinguish between Stochastic Gradient Descent with Momentum (SGDM) and Adam in terms of their convergence rates. We demonstrate that Adam achieves a faster convergence compared to SGDM under the condition of non-uniformly bounded smoothness. Our findings reveal that: (1) in deterministic environments, Adam can attain the known lower bound for the convergence rate of deterministic first-order optimizers, whereas the convergence rate of Gradient Descent with Momentum (GDM) has higher order dependence on the initial function value; (2) in stochastic setting, Adam's convergence rate upper bound matches the lower bounds of stochastic first-order optimizers, considering both the initial function value and the final error, whereas there are instances where SGDM fails to converge with any learning rate. These insights distinctly differentiate Adam and SGDM regarding their convergence rates. Additionally, by introducing a novel stopping-time based technique, we further prove that if we consider the minimum gradient norm during iterations, the corresponding convergence rate can match the lower bounds across all problem hyperparameters. The technique can also help proving that Adam with a specific hyperparameter scheduler is parameter-agnostic, which hence can be of independent interest.

Deciphering and integrating invariants for neural operator learning with various physical mechanisms

Neural operators have been explored as surrogate models for simulating physical systems to overcome the limitations of traditional partial differential equation (PDE) solvers. However, most existing operator learning methods assume that the data originate from a single physical mechanism, limiting their applicability and performance in more realistic scenarios. To this end, we propose Physical Invariant Attention Neural Operator (PIANO) to decipher and integrate the physical invariants (PI) for operator learning from the PDE series with various physical mechanisms. PIANO employs self-supervised learning to extract physical knowledge and attention mechanisms to integrate them into dynamic convolutional layers. Compared to existing techniques, PIANO can reduce the relative error by 13.6\%-82.2\% on PDE forecasting tasks across varying coefficients, forces, or boundary conditions. Additionally, varied downstream tasks reveal that the PI embeddings deciphered by PIANO align well with the underlying invariants in the PDE systems, verifying the physical significance of PIANO. The source code will be publicly available at: https://github.com/optray/PIANO.

Power-law Dynamic arising from machine learning

We study a kind of new SDE that was arisen from the research on optimization in machine learning, we call it power-law dynamic because its stationary distribution cannot have sub-Gaussian tail and obeys power-law. We prove that the power-law dynamic is ergodic with unique stationary distribution, provided the learning rate is small enough. We investigate its first exist time. In particular, we compare the exit times of the (continuous) power-law dynamic and its discretization. The comparison can help guide machine learning algorithm.

NeuralStagger: accelerating physics-constrained neural PDE solver with spatial-temporal decomposition

Neural networks have shown great potential in accelerating the solution of partial differential equations (PDEs). Recently, there has been a growing interest in introducing physics constraints into training neural PDE solvers to reduce the use of costly data and improve the generalization ability. However, these physics constraints, based on certain finite dimensional approximations over the function space, must resolve the smallest scaled physics to ensure the accuracy and stability of the simulation, resulting in high computational costs from large input, output, and neural networks. This paper proposes a general acceleration methodology called NeuralStagger by spatially and temporally decomposing the original learning tasks into several coarser-resolution subtasks. We define a coarse-resolution neural solver for each subtask, which requires fewer computational resources, and jointly train them with the vanilla physics-constrained loss by simply arranging their outputs to reconstruct the original solution. Due to the perfect parallelism between them, the solution is achieved as fast as a coarse-resolution neural solver. In addition, the trained solvers bring the flexibility of simulating with multiple levels of resolution. We demonstrate the successful application of NeuralStagger on 2D and 3D fluid dynamics simulations, which leads to an additional $10\sim100\times$ speed-up. Moreover, the experiment also shows that the learned model could be well used for optimal control.

Monte Carlo Neural Operator for Learning PDEs via Probabilistic Representation

Neural operators, which use deep neural networks to approximate the solution mappings of partial differential equation (PDE) systems, are emerging as a new paradigm for PDE simulation. The neural operators could be trained in supervised or unsupervised ways, i.e., by using the generated data or the PDE information. The unsupervised training approach is essential when data generation is costly or the data is less qualified (e.g., insufficient and noisy). However, its performance and efficiency have plenty of room for improvement. To this end, we design a new loss function based on the Feynman-Kac formula and call the developed neural operator Monte-Carlo Neural Operator (MCNO), which can allow larger temporal steps and efficiently handle fractional diffusion operators. Our analyses show that MCNO has advantages in handling complex spatial conditions and larger temporal steps compared with other unsupervised methods. Furthermore, MCNO is more robust with the perturbation raised by the numerical scheme and operator approximation. Numerical experiments on the diffusion equation and Navier-Stokes equation show significant accuracy improvement compared with other unsupervised baselines, especially for the vibrated initial condition and long-time simulation settings.