Physics-informed waveform inversion using pretrained wavefield neural operators

Full waveform inversion (FWI) is crucial for reconstructing high-resolution subsurface models, but it is often hindered, considering the limited data, by its null space resulting in low-resolution models, and more importantly, by its computational cost, especially if needed for real-time applications. Recent attempts to accelerate FWI using learned wavefield neural operators have shown promise in efficiency and differentiability, but typically suffer from noisy and unstable inversion performance. To address these limitations, we introduce a novel physics-informed FWI framework to enhance the inversion in accuracy while maintaining the efficiency of neural operator-based FWI. Instead of relying only on the L2 norm objective function via automatic differentiation, resulting in noisy model reconstruction, we integrate a physics constraint term in the loss function of FWI, improving the quality of the inverted velocity models. Specifically, starting with an initial model to simulate wavefields and then evaluating the loss over how much the resulting wavefield obeys the physical laws (wave equation) and matches the recorded data, we achieve a reduction in noise and artifacts. Numerical experiments using the OpenFWI and Overthrust models demonstrate our method's superior performance, offering cleaner and more accurate subsurface velocity than vanilla approaches. Considering the efficiency of the approach compared to FWI, this advancement represents a significant step forward in the practical application of FWI for real-time subsurface monitoring.

PhysicsCorrect: A Training-Free Approach for Stable Neural PDE Simulations

Neural networks have emerged as powerful surrogates for solving partial differential equations (PDEs), offering significant computational speedups over traditional methods. However, these models suffer from a critical limitation: error accumulation during long-term rollouts, where small inaccuracies compound exponentially, eventually causing complete divergence from physically valid solutions. We present PhysicsCorrect, a training-free correction framework that enforces PDE consistency at each prediction step by formulating correction as a linearized inverse problem based on PDE residuals. Our key innovation is an efficient caching strategy that precomputes the Jacobian and its pseudoinverse during an offline warm-up phase, reducing computational overhead by two orders of magnitude compared to standard correction approaches. Across three representative PDE systems -- Navier-Stokes fluid dynamics, wave equations, and the chaotic Kuramoto-Sivashinsky equation -- PhysicsCorrect reduces prediction errors by up to 100x while adding negligible inference time (under 5\%). The framework integrates seamlessly with diverse architectures including Fourier Neural Operators, UNets, and Vision Transformers, effectively transforming unstable neural surrogates into reliable simulation tools that bridge the gap between deep learning's computational efficiency and the physical fidelity demanded by practical scientific applications.

Geological and Well prior assisted full waveform inversion using conditional diffusion models

Full waveform inversion (FWI) often faces challenges due to inadequate seismic observations, resulting in band-limited and geologically inaccurate inversion results. Incorporating prior information from potential velocity distributions, well-log information, and our geological knowledge and expectations can significantly improve FWI convergence to a realistic model. While diffusion-regularized FWI has shown improved performance compared to conventional FWI by incorporating the velocity distribution prior, it can benefit even more by incorporating well-log information and other geological knowledge priors. To leverage this fact, we propose a geological class and well-information prior-assisted FWI using conditional diffusion models. This method seamlessly integrates multi-modal information into FWI, simultaneously achieving data fitting and universal geologic and geophysics prior matching, which is often not achieved with traditional regularization methods. Specifically, we propose to combine conditional diffusion models with FWI, where we integrate well-log data and geological class conditions into these conditional diffusion models using classifier-free guidance for multi-modal prior matching beyond the original velocity distribution prior. Numerical experiments on the OpenFWI datasets and field marine data demonstrate the effectiveness of our method compared to conventional FWI and the unconditional diffusion-regularized FWI.

Diffusion-based subsurface multiphysics monitoring and forecasting

Carbon capture and storage (CCS) plays a crucial role in mitigating greenhouse gas emissions, particularly from industrial outputs. Using seismic monitoring can aid in an accurate and robust monitoring system to ensure the effectiveness of CCS and mitigate associated risks. However, conventional seismic wave equation-based approaches are computationally demanding, which hinders real-time applications. In addition to efficiency, forecasting and uncertainty analysis are not easy to handle using such numerical-simulation-based approaches. To this end, we propose a novel subsurface multiphysics monitoring and forecasting framework utilizing video diffusion models. This approach can generate high-quality representations of CO$2$ evolution and associated changes in subsurface elastic properties. With reconstruction guidance, forecasting and inversion can be achieved conditioned on historical frames and/or observational data. Meanwhile, due to the generative nature of the approach, we can quantify uncertainty in the prediction. Tests based on the Compass model show that the proposed method successfully captured the inherently complex physical phenomena associated with CO$_2$ monitoring, and it can predict and invert the subsurface elastic properties and CO$_2$ saturation with consistency in their evolution.

Controllable seismic velocity synthesis using generative diffusion models

Accurate seismic velocity estimations are vital to understanding Earth's subsurface structures, assessing natural resources, and evaluating seismic hazards. Machine learning-based inversion algorithms have shown promising performance in regional (i.e., for exploration) and global velocity estimation, while their effectiveness hinges on access to large and diverse training datasets whose distributions generally cover the target solutions. Additionally, enhancing the precision and reliability of velocity estimation also requires incorporating prior information, e.g., geological classes, well logs, and subsurface structures, but current statistical or neural network-based methods are not flexible enough to handle such multi-modal information. To address both challenges, we propose to use conditional generative diffusion models for seismic velocity synthesis, in which we readily incorporate those priors. This approach enables the generation of seismic velocities that closely match the expected target distribution, offering datasets informed by both expert knowledge and measured data to support training for data-driven geophysical methods. We demonstrate the flexibility and effectiveness of our method through training diffusion models on the OpenFWI dataset under various conditions, including class labels, well logs, reflectivity images, as well as the combination of these priors. The performance of the approach under out-of-distribution conditions further underscores its generalization ability, showcasing its potential to provide tailored priors for velocity inverse problems and create specific training datasets for machine learning-based geophysical applications.

Physics-informed neural wavefields with Gabor basis functions

Recently, Physics-Informed Neural Networks (PINNs) have gained significant attention for their versatile interpolation capabilities in solving partial differential equations (PDEs). Despite their potential, the training can be computationally demanding, especially for intricate functions like wavefields. This is primarily due to the neural-based (learned) basis functions, biased toward low frequencies, as they are dominated by polynomial calculations, which are not inherently wavefield-friendly. In response, we propose an approach to enhance the efficiency and accuracy of neural network wavefield solutions by modeling them as linear combinations of Gabor basis functions that satisfy the wave equation. Specifically, for the Helmholtz equation, we augment the fully connected neural network model with an adaptable Gabor layer constituting the final hidden layer, employing a weighted summation of these Gabor neurons to compute the predictions (output). These weights/coefficients of the Gabor functions are learned from the previous hidden layers that include nonlinear activation functions. To ensure the Gabor layer's utilization across the model space, we incorporate a smaller auxiliary network to forecast the center of each Gabor function based on input coordinates. Realistic assessments showcase the efficacy of this novel implementation compared to the vanilla PINN, particularly in scenarios involving high-frequencies and realistic models that are often challenging for PINNs.

GaborPINN: Efficient physics informed neural networks using multiplicative filtered networks

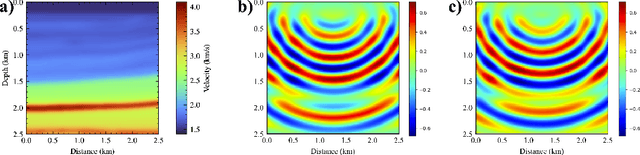
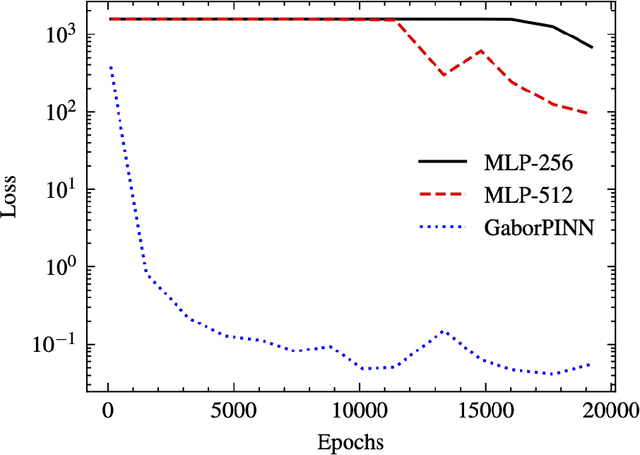
The computation of the seismic wavefield by solving the Helmholtz equation is crucial to many practical applications, e.g., full waveform inversion. Physics-informed neural networks (PINNs) provide functional wavefield solutions represented by neural networks (NNs), but their convergence is slow. To address this problem, we propose a modified PINN using multiplicative filtered networks, which embeds some of the known characteristics of the wavefield in training, e.g., frequency, to achieve much faster convergence. Specifically, we use the Gabor basis function due to its proven ability to represent wavefields accurately and refer to the implementation as GaborPINN. Meanwhile, we incorporate prior information on the frequency of the wavefield into the design of the method to mitigate the influence of the discontinuity of the represented wavefield by GaborPINN. The proposed method achieves up to a two-magnitude increase in the speed of convergence as compared with conventional PINNs.

A prior regularized full waveform inversion using generative diffusion models

Full waveform inversion (FWI) has the potential to provide high-resolution subsurface model estimations. However, due to limitations in observation, e.g., regional noise, limited shots or receivers, and band-limited data, it is hard to obtain the desired high-resolution model with FWI. To address this challenge, we propose a new paradigm for FWI regularized by generative diffusion models. Specifically, we pre-train a diffusion model in a fully unsupervised manner on a prior velocity model distribution that represents our expectations of the subsurface and then adapt it to the seismic observations by incorporating the FWI into the sampling process of the generative diffusion models. What makes diffusion models uniquely appropriate for such an implementation is that the generative process retains the form and dimensions of the velocity model. Numerical examples demonstrate that our method can outperform the conventional FWI with only negligible additional computational cost. Even in cases of very sparse observations or observations with strong noise, the proposed method could still reconstruct a high-quality subsurface model. Thus, we can incorporate our prior expectations of the solutions in an efficient manner. We further test this approach on field data, which demonstrates the effectiveness of the proposed method.

Microseismic source imaging using physics-informed neural networks with hard constraints

Microseismic source imaging plays a significant role in passive seismic monitoring. However, such a process is prone to failure due to the aliasing problem when dealing with sparse measured data. Thus, we propose a direct microseismic imaging framework based on physics-informed neural networks (PINNs), which can generate focused source images, even with very sparse recordings. We use the PINNs to represent a multi-frequency wavefield and then apply the inverse Fourier transform to extract the source image. Specially, we modify the representation of the frequency-domain wavefield to inherently satisfy the boundary conditions (the measured data on the surface) by means of the hard constraint, which helps to avoid the difficulty in balancing the data and PDE losses in PINNs. Furthermore, we propose the causality loss implementation with respect to depth to enhance the convergence of PINNs. The numerical experiments on the Overthrust model show that the method can admit reliable and accurate source imaging for single- or multiple- sources and even in passive monitoring settings. Then, we further apply our method on the hydraulic fracturing field data, and demonstrate that our method can correctly image the source.

Efficient physics-informed neural networks using hash encoding

Physics-informed neural networks (PINNs) have attracted a lot of attention in scientific computing as their functional representation of partial differential equation (PDE) solutions offers flexibility and accuracy features. However, their training cost has limited their practical use as a real alternative to classic numerical methods. Thus, we propose to incorporate multi-resolution hash encoding into PINNs to improve the training efficiency, as such encoding offers a locally-aware (at multi resolution) coordinate inputs to the neural network. Borrowed from the neural representation field community (NeRF), we investigate the robustness of calculating the derivatives of such hash encoded neural networks with respect to the input coordinates, which is often needed by the PINN loss terms. We propose to replace the automatic differentiation with finite-difference calculations of the derivatives to address the discontinuous nature of such derivatives. We also share the appropriate ranges for the hash encoding hyperparameters to obtain robust derivatives. We test the proposed method on three problems, including Burgers equation, Helmholtz equation, and Navier-Stokes equation. The proposed method admits about a 10-fold improvement in efficiency over the vanilla PINN implementation.