GaborPINN: Efficient physics informed neural networks using multiplicative filtered networks
Paper and Code
Aug 10, 2023

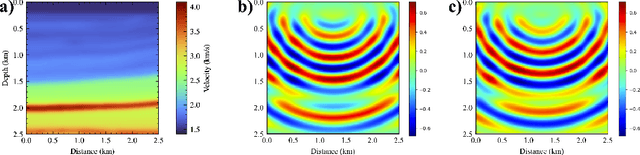
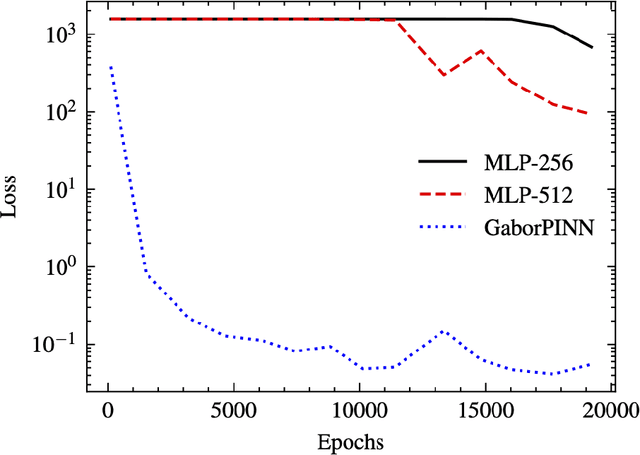
The computation of the seismic wavefield by solving the Helmholtz equation is crucial to many practical applications, e.g., full waveform inversion. Physics-informed neural networks (PINNs) provide functional wavefield solutions represented by neural networks (NNs), but their convergence is slow. To address this problem, we propose a modified PINN using multiplicative filtered networks, which embeds some of the known characteristics of the wavefield in training, e.g., frequency, to achieve much faster convergence. Specifically, we use the Gabor basis function due to its proven ability to represent wavefields accurately and refer to the implementation as GaborPINN. Meanwhile, we incorporate prior information on the frequency of the wavefield into the design of the method to mitigate the influence of the discontinuity of the represented wavefield by GaborPINN. The proposed method achieves up to a two-magnitude increase in the speed of convergence as compared with conventional PINNs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge